【Python–NetworkX】函数说明+代码讲解

文章目录

【Python--NetworkX】函数说明+代码讲解
- 1. 介绍
- - 1.1 前言
  - 1.2 图的类型（Graph Types）
  - 1.3 常用方法
- 2. 代码示例

1. 介绍

1.1 前言

NetworkX是复杂网络研究领域中的常用Python包。

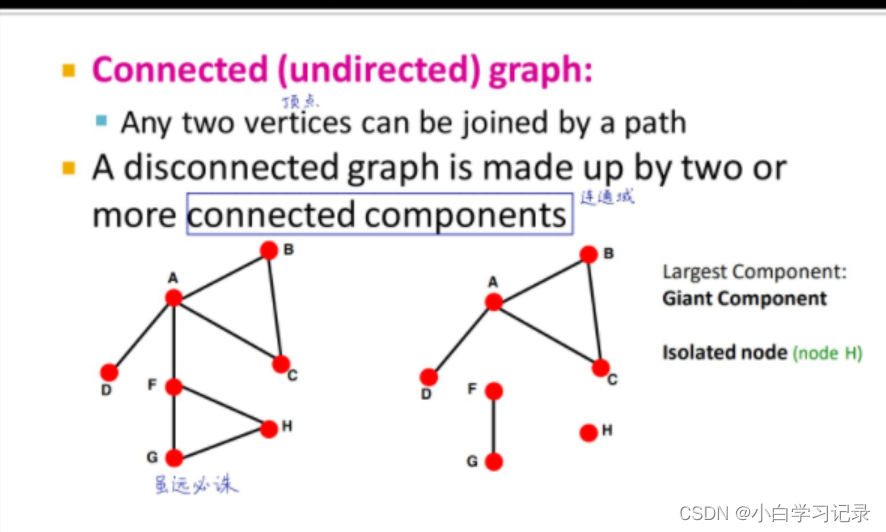
1.2 图的类型（Graph Types）

允许以可哈希的object作为节点，任何Python object作为边属性。

如何选择使用哪种图：

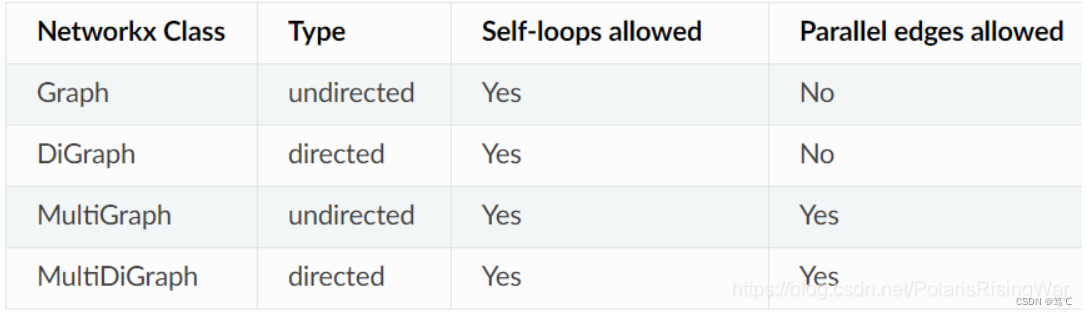
这里解释一下什么是平行边：连接一对顶点的两条边叫做平行边，即，无向图中，两个顶点间有多条边，他们叫做平行边，打个比方，北京和上海直接可以是公路、铁路、飞机，那么他们互为平行边。

1.3 常用方法

创建一个空的图
1）无向图：G = nx.Graph()
2）有向图：DG = nx.DiGraph()
将有向图转换为无向图：G = nx.Graph(DG)
图是否有向：G.is_directed() 返回布尔值
添加节点
1)直接添加一个节点（任何object都可以作为节点，包括另一个图）G.add_node(1)、G.add_node(DG)
2)从任何容器加点：a list, dict, set or even the lines from a file or the nodes from another graph…；G.add_nodes_from() 或 nx.path_graph()
添加边
1）添加一条边 G.add_edge(u, v)
2）添加一个边的列表 G.add_edges_from([(1, 2), (1, 3)])
3）添加一个边的collection G.add_edges_from(H.edges)
4）如果添加的边的点不存在于图中，会自动添上相应节点而不报错
属性attribute
1）图的节点/边/图都可以在关联的attribute字典中以键值对key/value形式存储attribute（key一定要是可哈希的）
2）默认情况下属性字典是空的
3）可以通过add_edge() add_node() 方法或直接操作分别名为graph edges nodes的属性字典来进行操作

2. 代码示例

import networkx as nx
import numpy as np 

#定义图的节点和边 
nodes=['0','1','2','3','4','5','a','b','c'] 
edges=[('0','0',1),('0','1',1),('0','5',1),('0','5',2),('1','2',3),('1','4',5),('2','1',7),('2','4',6),('a','b',0.5),('b','c',0.5),('c','a',0.5)] 

plt.subplots(1,2,figsize=(10,3)) 

#定义一个无向图和有向图 
G1 = nx.Graph() 
G1.add_nodes_from(nodes) 
G1.add_weighted_edges_from(edges) 
 
G2 = nx.DiGraph() 
G2.add_nodes_from(nodes) 
G2.add_weighted_edges_from(edges) 
 
pos1=nx.circular_layout(G1) 
pos2=nx.circular_layout(G2) 
 
#画出无向图和有向图 
plt.subplot(121) 
nx.draw(G1,pos1, with_labels=True, font_weight='bold') 
plt.title('无向图',fontproperties=myfont) 
plt.axis('on') 
plt.xticks([]) 
plt.yticks([]) 

plt.subplot(122) 
nx.draw(G2,pos2, with_labels=True, font_weight='bold') 
plt.title('有向图',fontproperties=myfont) 
plt.axis('on') 
plt.xticks([]) 
plt.yticks([]) 

plt.show() 

 #控制numpy输出小数位数 
np.set_printoptions(precision=3)  
 
#邻接矩阵 
A = nx.adjacency_matrix(G1) 
print('邻接矩阵:\n',A.todense()) 
邻接矩阵: 
 [[0.  0.  0.  0.  5.  0.  0.  0.  6. ] 
 [0.  0.  0.  2.  0.  0.  0.  0.  0. ] 
 [0.  0.  0.  0.  0.  0.5 0.5 0.  0. ] 
 [0.  2.  0.  1.  1.  0.  0.  0.  0. ] 
 [5.  0.  0.  1.  0.  0.  0.  0.  7. ] 
 [0.  0.  0.5 0.  0.  0.  0.5 0.  0. ] 
 [0.  0.  0.5 0.  0.  0.5 0.  0.  0. ] 
 [0.  0.  0.  0.  0.  0.  0.  0.  0. ] 
 [6.  0.  0.  0.  7.  0.  0.  0.  0. ]] 

#关联矩阵 
I = nx.incidence_matrix(G1) 
print('\n关联矩阵:\n',I.todense()) 
关联矩阵: 
 [[1. 1. 0. 0. 0. 0. 0. 0. 0.] 
  [0. 0. 1. 0. 0. 0. 0. 0. 0.] 
 [0. 0. 0. 1. 1. 0. 0. 0. 0.] 
  [0. 0. 1. 0. 0. 1. 0. 0. 0.] 
  [0. 1. 0. 0. 0. 1. 0. 1. 0.] 
 [0. 0. 0. 1. 0. 0. 0. 0. 1.] 
 [0. 0. 0. 0. 1. 0. 0. 0. 1.] 
 [0. 0. 0. 0. 0. 0. 0. 0. 0.] 
 [1. 0. 0. 0. 0. 0. 0. 1. 0.]] 

#拉普拉斯矩阵 
L=nx.laplacian_matrix(G1) 
print('\n拉普拉斯矩阵:\n',L.todense()) 
拉普拉斯矩阵: 
  [[11.   0.   0.   0.  -5.   0.   0.   0.  -6. ] 
 [ 0.   2.   0.  -2.   0.   0.   0.   0.   0. ] 
 [ 0.   0.   1.   0.   0.  -0.5 -0.5  0.   0. ] 
 [ 0.  -2.   0.   3.  -1.   0.   0.   0.   0. ] 
 [-5.   0.   0.  -1.  13.   0.   0.   0.  -7. ] 
 [ 0.   0.  -0.5  0.   0.   1.  -0.5  0.   0. ] 
 [ 0.   0.  -0.5  0.   0.  -0.5  1.   0.   0. ] 
 [ 0.   0.   0.   0.   0.   0.   0.   0.   0. ] 
  [-6.   0.   0.   0.  -7.   0.   0.   0.  13. ]] 

#标准化的拉普拉斯矩阵 
NL=nx.normalized_laplacian_matrix(G1) 
print('标准化的拉普拉斯矩阵:\n',NL.todense()) 
标准化的拉普拉斯矩阵: 
  [[ 1.     0.     0.     0.    -0.418  0.     0.     0.    -0.502] 
  [ 0.     1.     0.    -0.707  0.     0.     0.     0.     0.   ] 
  [ 0.     0.     1.     0.     0.    -0.5   -0.5    0.     0.   ] 
  [ 0.    -0.707  0.     0.75  -0.139  0.     0.     0.     0.   ] 
  [-0.418  0.     0.    -0.139  1.     0.     0.     0.    -0.538] 
  [ 0.     0.    -0.5    0.     0.     1.    -0.5    0.     0.   ] 
  [ 0.     0.    -0.5    0.     0.    -0.5    1.     0.     0.   ] 
  [ 0.     0.     0.     0.     0.     0.     0.     0.     0.   ] 
  [-0.502  0.     0.     0.    -0.538  0.     0.     0.     1.   ]] 

#有向图拉普拉斯矩阵 
DL=nx.directed_laplacian_matrix(G2) 
print('\n有向拉普拉斯矩阵:\n',DL) 
有向拉普拉斯矩阵: 
  [[ 0.889 -0.117 -0.029 -0.087 -0.319 -0.029 -0.029 -0.129 -0.242] 
  [-0.117  0.889 -0.026 -0.278 -0.051 -0.026 -0.026 -0.114 -0.056] 
  [-0.029 -0.026  0.994 -0.012 -0.009 -0.481 -0.481 -0.025 -0.01 ] 
  [-0.087 -0.278 -0.012  0.757 -0.097 -0.012 -0.012 -0.052 -0.006] 
  [-0.319 -0.051 -0.009 -0.097  0.994 -0.009 -0.009 -0.041 -0.434] 
  [-0.029 -0.026 -0.481 -0.012 -0.009  0.994 -0.481 -0.025 -0.01 ] 
  [-0.029 -0.026 -0.481 -0.012 -0.009 -0.481  0.994 -0.025 -0.01 ] 
  [-0.129 -0.114 -0.025 -0.052 -0.041 -0.025 -0.025  0.889 -0.045] 
  [-0.242 -0.056 -0.01  -0.006 -0.434 -0.01  -0.01  -0.045  0.994]] 

#拉普拉斯算子的特征值 
LS=nx.laplacian_spectrum(G1) 
print('\n拉普拉斯算子的特征值:\n',LS) 
拉普拉斯算子的特征值: 
 [-1.436e-15  0.000e+00  4.610e-16  7.000e-01  1.500e+00  1.500e+00 
  4.576e+00  1.660e+01  2.013e+01] 

#邻接矩阵的特征值 
AS=nx.adjacency_spectrum(G1) 
print('邻接矩阵的特征值:\n',AS) 
邻接矩阵的特征值: 
  [12.068+0.000e+00j  2.588+0.000e+00j -7.219+0.000e+00j -4.925+0.000e+00j 
 -1.513+0.000e+00j  1.   +0.000e+00j -0.5  +2.393e-17j -0.5  -2.393e-17j0.  +0.000e+00j]

#无向图的代数连通性 
AC=nx.algebraic_connectivity(G1) 
print('无向图的代数连通性:\n',AC) 
无向图的代数连通性: 
  0.0 
  
#图的光谱排序 
SO=nx.spectral_ordering(G1) 
print('图的光谱排序:\n',SO) 
图的光谱排序: 
 ['4', '2', '1', '0', '5', 'b', 'c', 'a', '3']