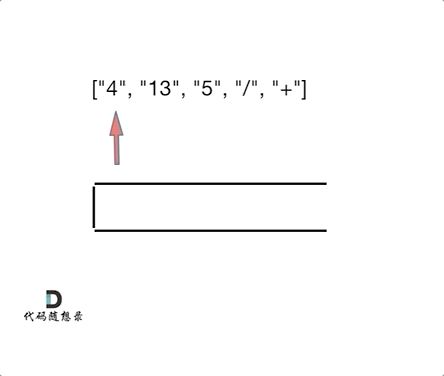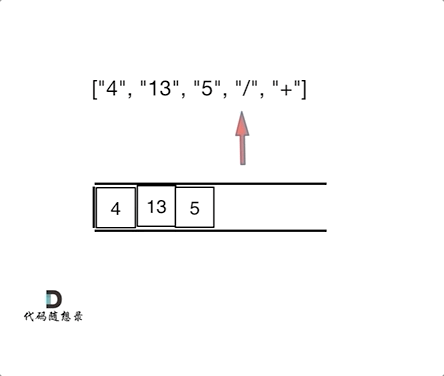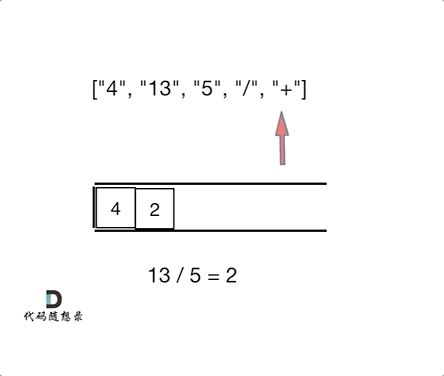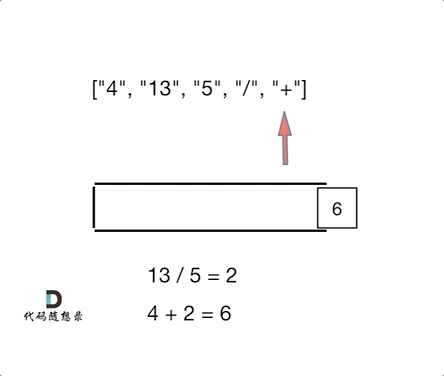
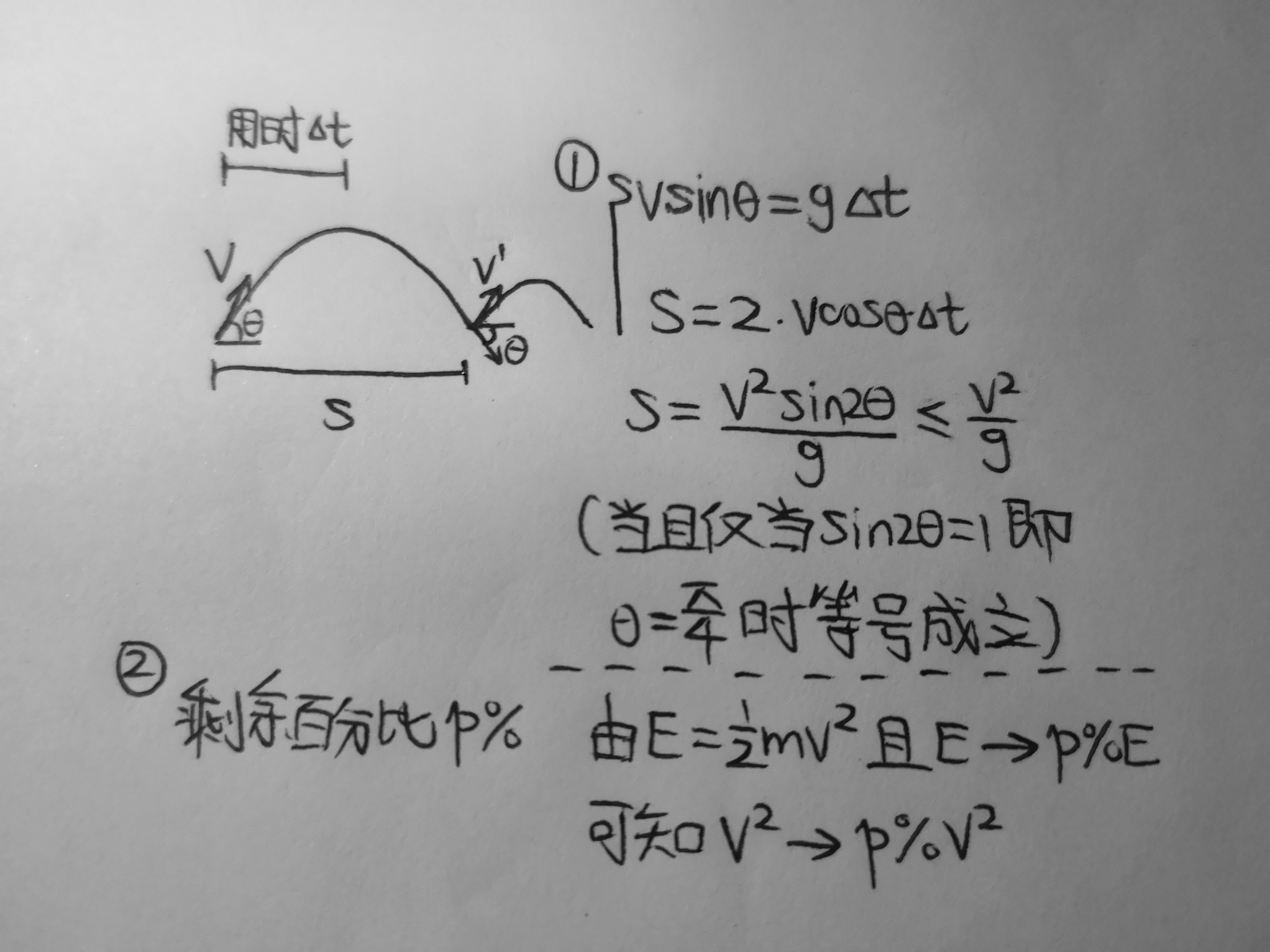
今天主要学习了哈夫曼树。

哈夫曼树

哈夫曼树是二叉树的一种，它是一种WPL最优二叉树。

叶子结点（也称叶节点）：指的是自己下面不再连接有节点的节点（即末端），称为叶子节点（又称为终端结点）。

WPL是二叉树的带权路径长度，是指所有叶节点的路径长度乘以当前叶节点的权值之和，打一个比方：

下面有一个字符串，我们以字母出现次数作为权值，a所对应的权值4，我们需要构造一个二叉树，最优WPL的二叉树。 

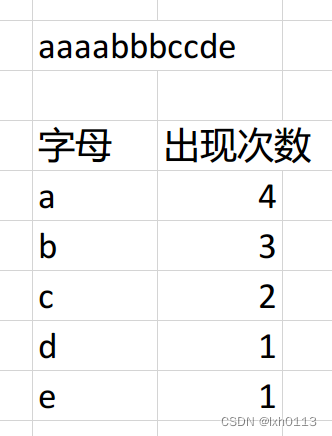
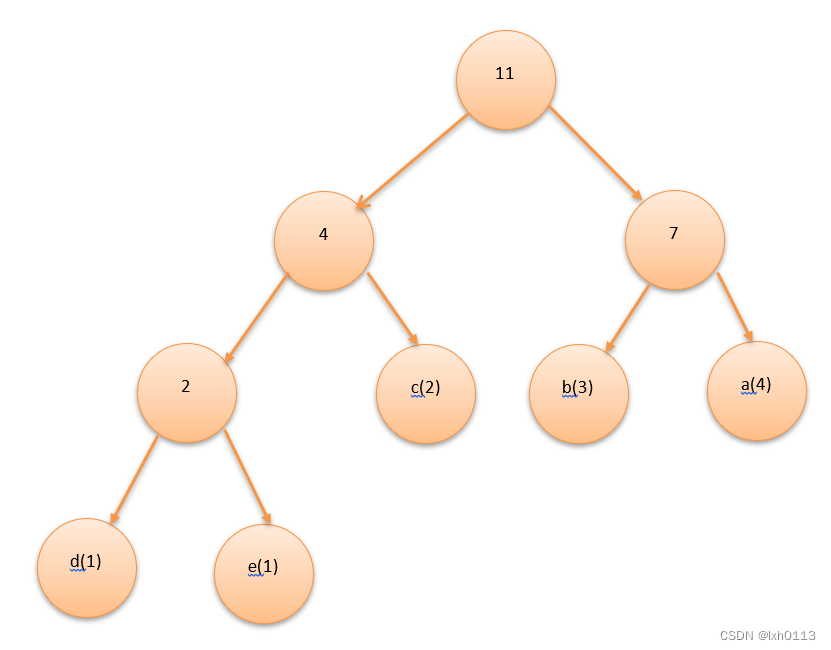
这是最优的哈夫曼树了，你再也找不到一个比这更优的了，那么它的WPL值为

1*3+1*3+2*2+3*2+4*2=24

还有一个更简洁的计算方法就是将图中的非叶结点值相加，11+4+7+2=24.

存储元素的结点为2*n-1，我们原来有5个结点，最后变成了9个结点

这很巧妙了，接下来讲解如何构建一个哈夫曼树。

在表中找俩个最小值作为结点的左右孩子

很明显是d e所代表的权值，新结点的权值为俩孩子的权值之和，即是2

 

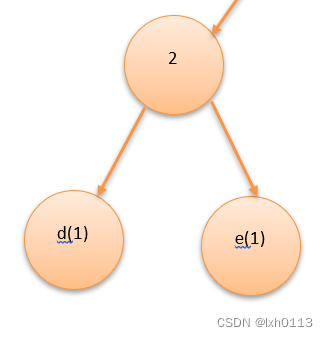
我们需要更新权值的数组，就是删除数组中c d的权值，把新节点的权值写入数组

 

再继续找俩最小值，是c代表的2和另外一个没名字的结点，从下往上插入哦。

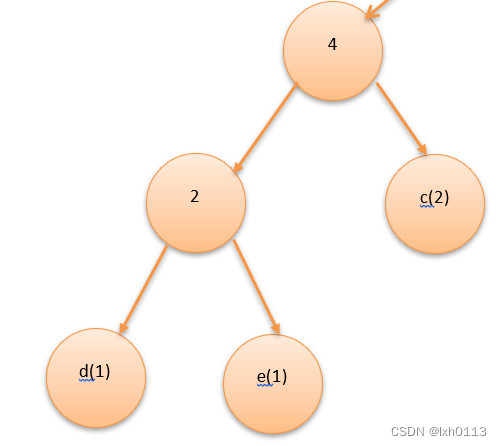
重复这些操作知道权值数组没有数值，最后就会变成开篇讲的那样子。

构建哈夫曼树，主要是为了满足哈夫曼编码。

哈夫曼编码是编码的一种，它是用来压缩文本的，主要压缩一段较长并且重复率较高的代码。

之所以那样子建立树，是为了将出现次数多的字符放在前面，出现次数少的字符放在后面，保证访问率的快慢。

 

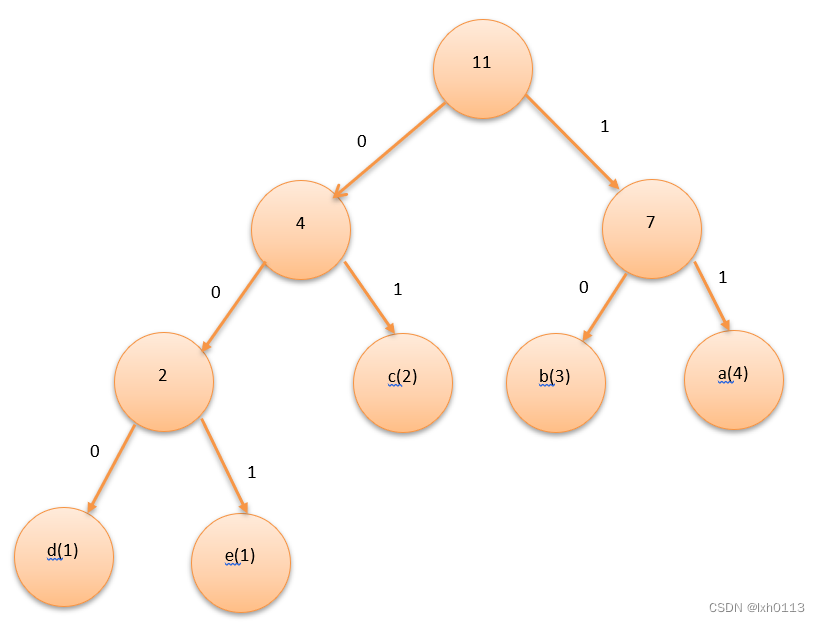
如上面所示将左边赋值为0，右边为1，我们可以发现一个特性，叶节点所构成的值，是不会有重复前缀的。（当然末尾俩个端点是会有一样的前缀，我们通常按照大小将其左右，左边是较小的，右边的较大的）

 

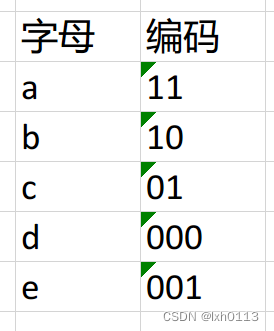
继而会变成上面那样子，我写的时候带了空格为了美观，实际存储时不带的，我们只需要根据哈夫曼树，按顺序找第一次出现的叶节点的编码，就可以凑成以上的字符串，（你可以自己试一试）。

哈夫曼编码是不等长编码。在一段长的重复率较高的文章特别适用。