---

1、图机器学习导论

1.1图神经网络与普通神经网络的异同

传统神经网络
以往：随着机器学习、深度学习的发展，语音、图像、自然语言处理逐渐取得了很大的突破，然而语音、图像、文本都是很简单的序列或者网格数据，是很结构化的数据，深度学习很善于处理该种类型的数据。

---

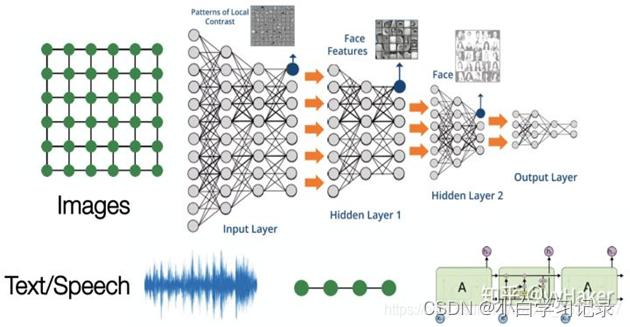
图神经网络
现实世界：并不是所有的事物都可以表示成一个序列或者一个网格，例如社交网络、知识图谱、复杂的文件系统等，也就是说很多事物都是非结构化的。

---

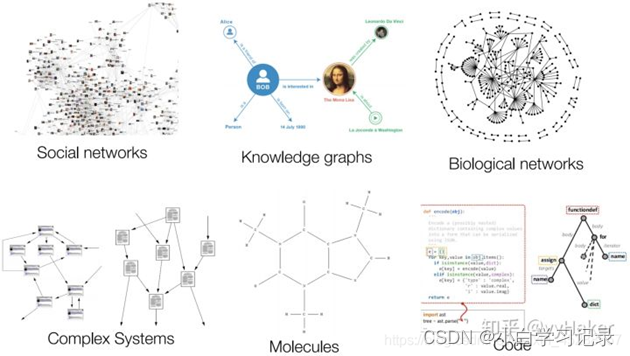
2、图的基本表示和特征工程

2.1 图的基本表示

内容：
图的本体设计
图的种类（有向、无向、异质、二分、连接带权重）
节点连接数
图的基本表示-邻接矩阵
图的基本表示-连接列表和邻接列表
图的联通性

---

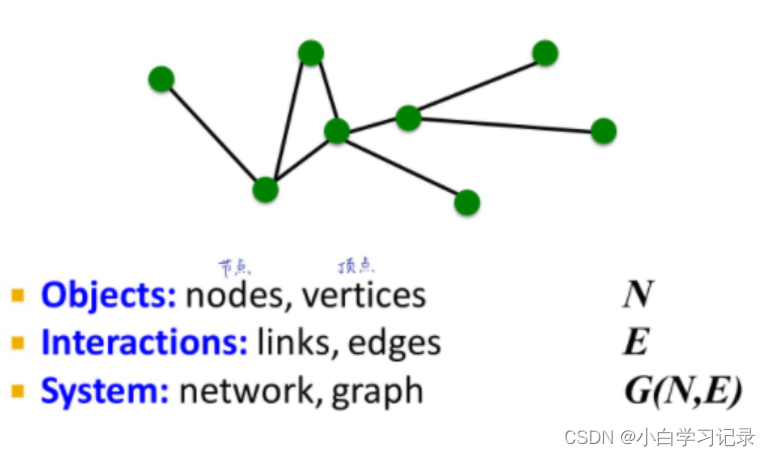
2.1.1 图的本体设计

• 如何设计图的本体设计取决于将来想解决什么问题。
• 从中心点出发，将所需要的要素根据中心点延伸。来判断节点种类和个数
  

---

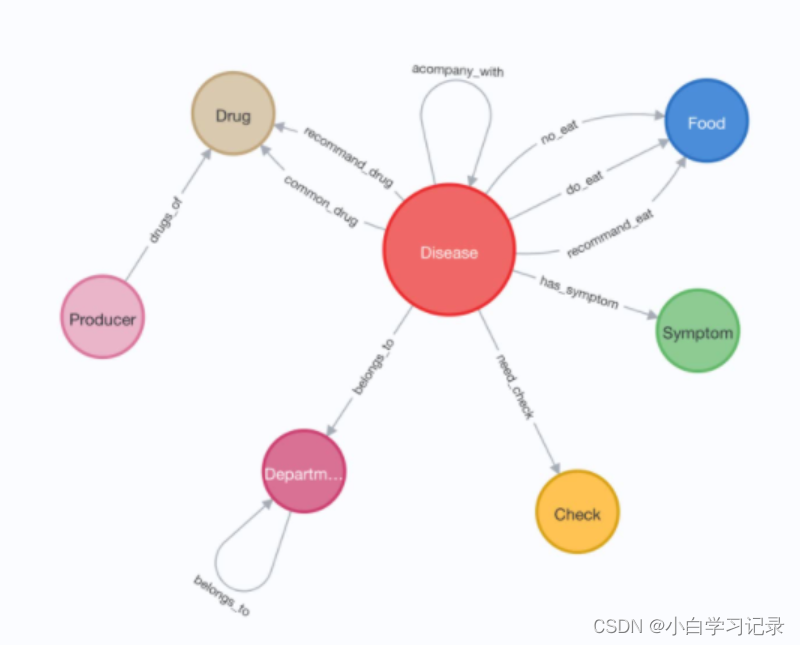
2.1.2 图的种类

图的种类：（有向、无向、异质、二分、连接带权重）

---

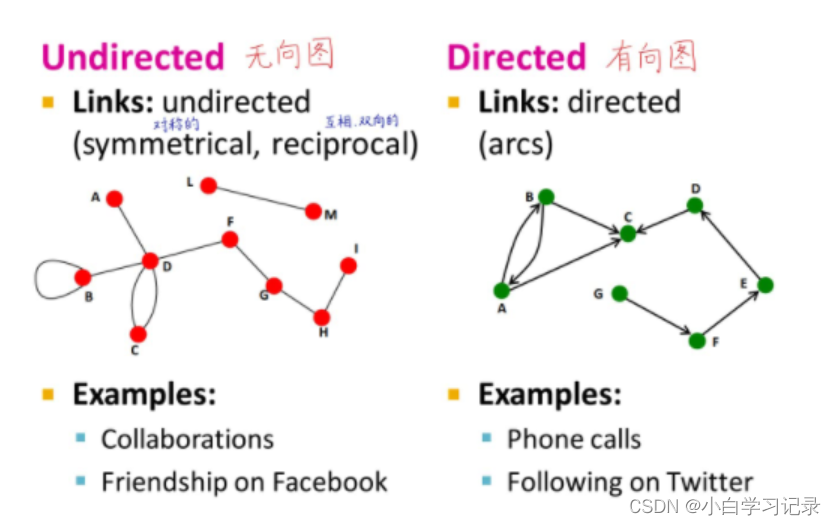
异质图

同质图：只包含一类型节点和一类型边
一个异质图G由一组节点V和一组边E构成。其中每个节点和每条边都对应着一种类型.T就是表示节点类型集合，R表示边类型集合。

二分图：G={V,E}
节点集V可以分为两种不相交的子集V1,V2。而E中的每条边都连接着V1中的一个节点和V2中的一个节点。二分图广泛用于捕获不同对象之间的互动。

---

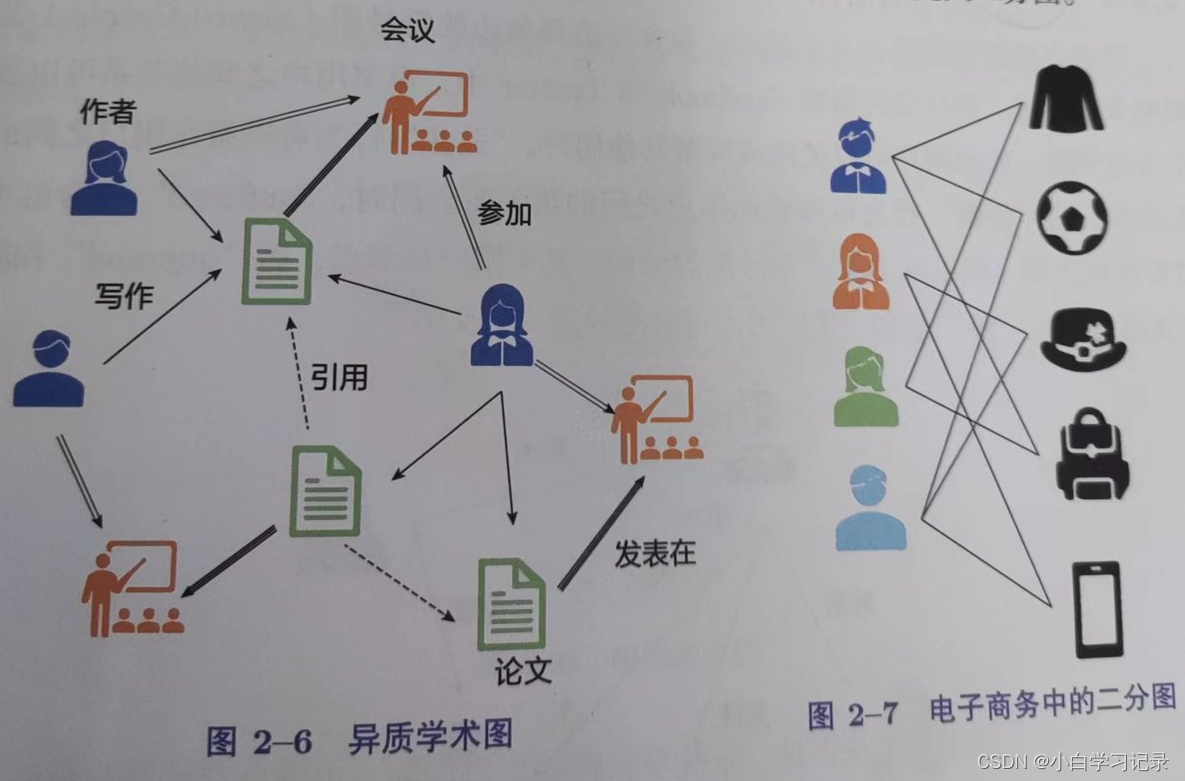
二分图展开

---

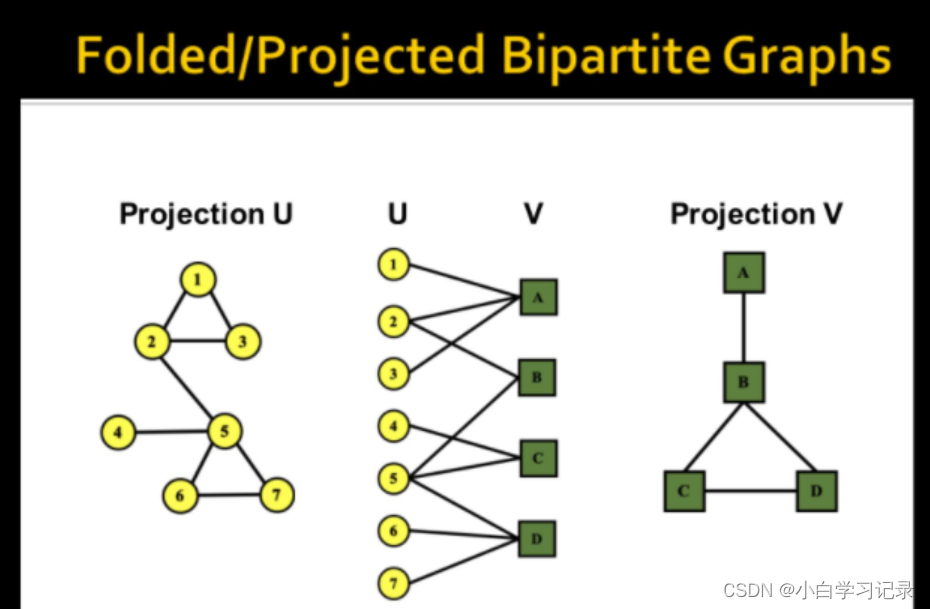
2.1.3节点连接数（度）

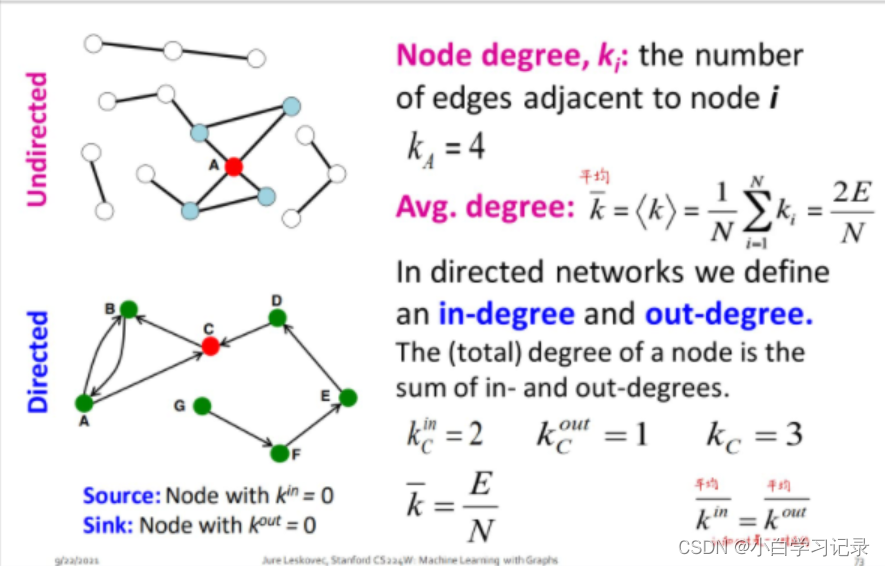
度：表示这个节点和其他相邻节点的次数

---

2.1.4图的基本表示（邻接矩阵）节点数量少使用

---

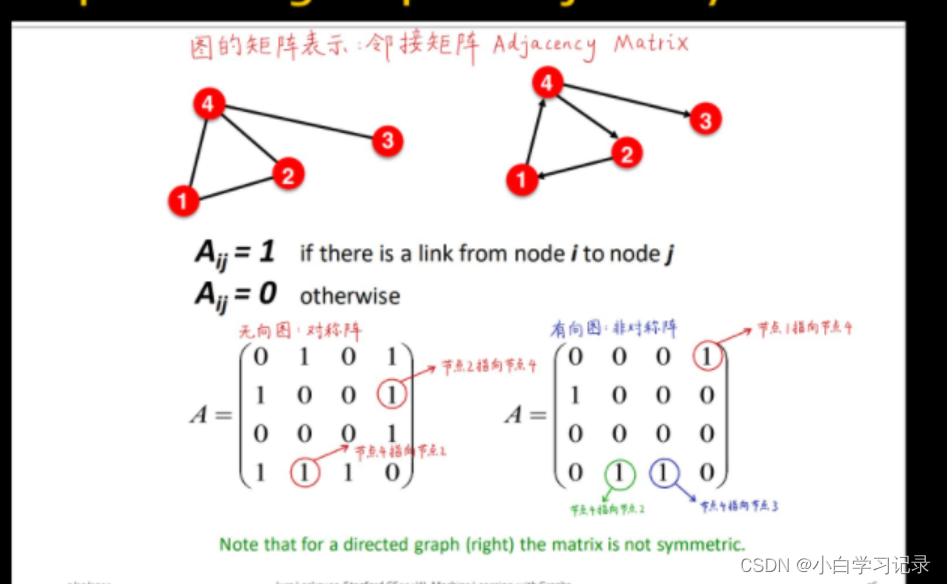
2.1.5图的基本表示（连接列表和邻接列表）数量巨大采用

---

---

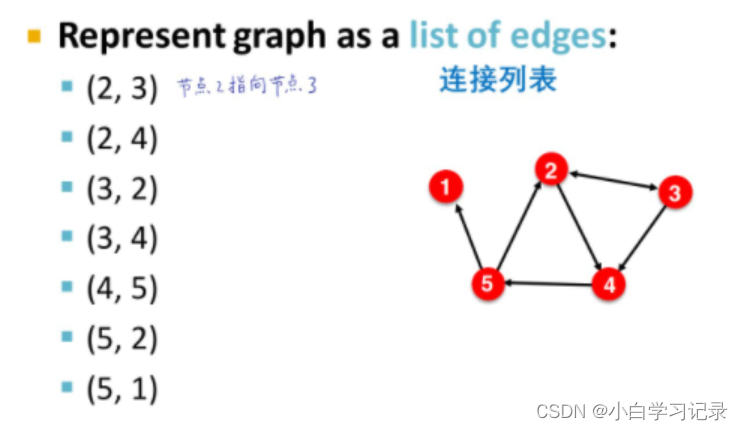
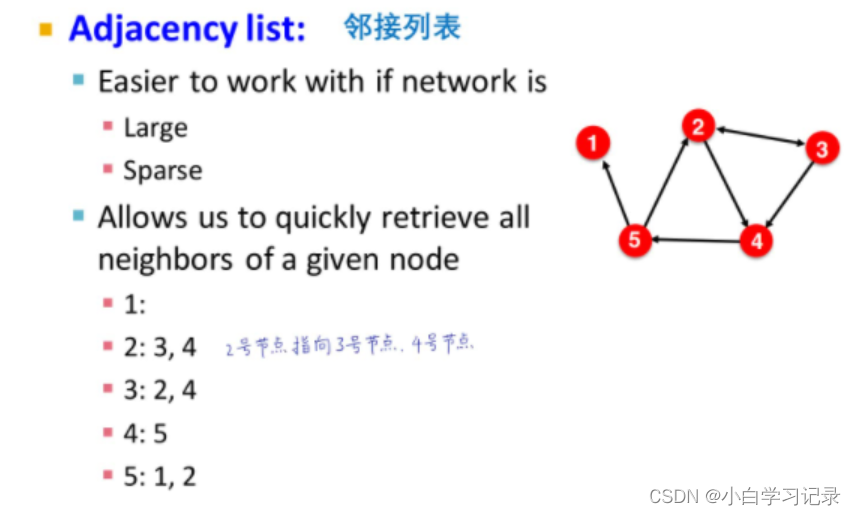
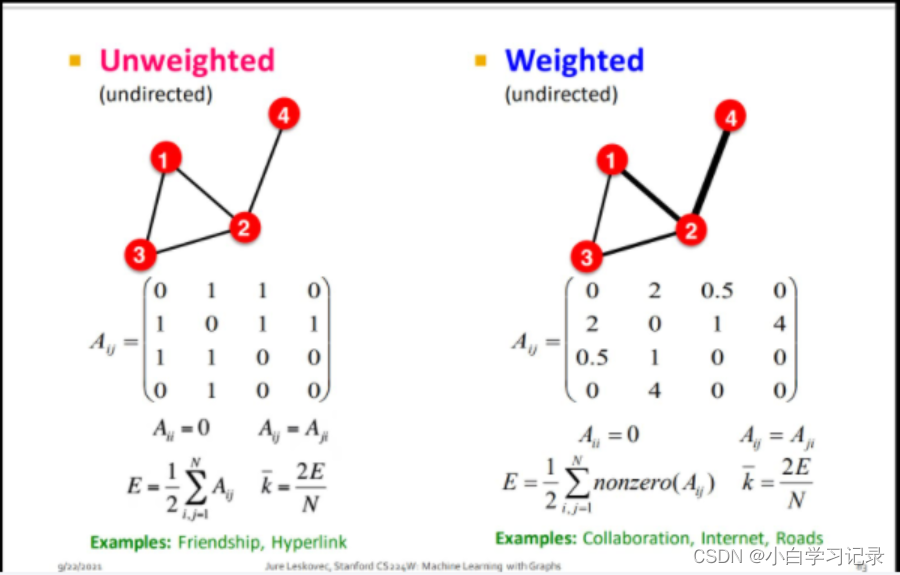
带权重的图

---

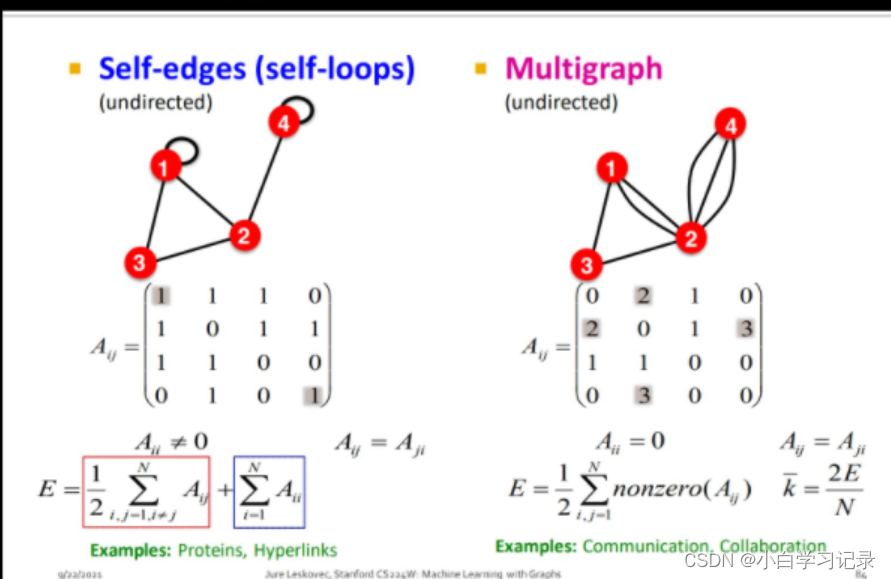
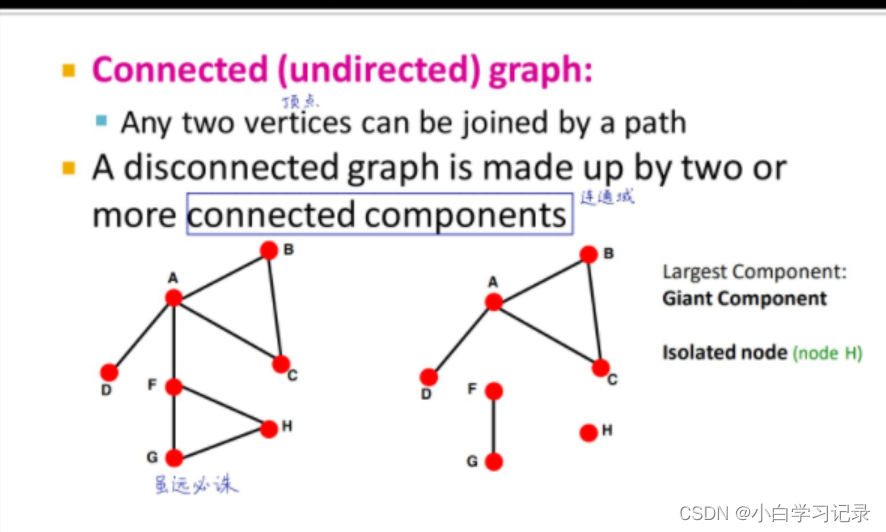
2.1.6图的连通性

• 如果一个图任意两节点间，总有一条路可以触达，称为连通图
• 否则称为非连通图，由多个连通域组成

---