目录
问题描述:
实现代码与解析:
回溯:
原理思路:
问题描述:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a" 输出:[["a"]]
实现代码与解析:
回溯:
class Solution {
public:
//判断是否为回文
bool isPalindrome(string s)
{
int head=0;//头指针
int end=s.size()-1;//尾指针
while(head<end)
{
if(s[head]!=s[end]) return false;
head++;
end--;
}
return true;
}
vector<string> path;
vector<vector<string>> result;//记录结果
void backtrack(string s,int startIndex)
{
//起始位置大于字符串大小,说明已经找到了分割结果
if(startIndex==s.size())
{
result.push_back(path);
return;
}
for(int i=startIndex;i<s.size();i++)
{
string str=s.substr(startIndex,i-startIndex+1);//切割字符串
//判断是否为回文
if(isPalindrome(str))
{
path.push_back(str);
}
else continue;
backtrack(s,i+1);//递归
path.pop_back();//回溯
}
return;
}
vector<vector<string>> partition(string s)
{
backtrack(s,0);
return result;
}
};原理思路:
首先题目为分割回文串,首先我们要知道什么是回文串,就像aba这种正反读相同的串。
这题肯定是要判断一个子串是否为回文串的,所以我们先写出判断回文串的函数。其实就是简单的双指针,一个前,一个后,大家看代码就能看懂。
//判断是否为回文
bool isPalindrome(string s)
{
int head=0;//头指针
int end=s.size()-1;//尾指针
while(head<end)
{
if(s[head]!=s[end]) return false;
head++;
end--;
}
return true;
}此题与组合题相似,只不过组合题每次循环就选取一个数,而此题每次循环选取的是截取的子串。
还是先确定递归终止条件,如果index等于字符串s大小,说明已经全部切割好了,第一次写此题,大部分人想的应该是,终止条件是判断切割的结果是否都为回文串,其实这样写就麻烦了,这里我们把判断回文的代码写在递归逻辑里,这样不仅写的方便,而且运行用的时间也会短很多。
然后就是如何切割,其实每层循环的切割的子串就是起始位置到循环到的位置。
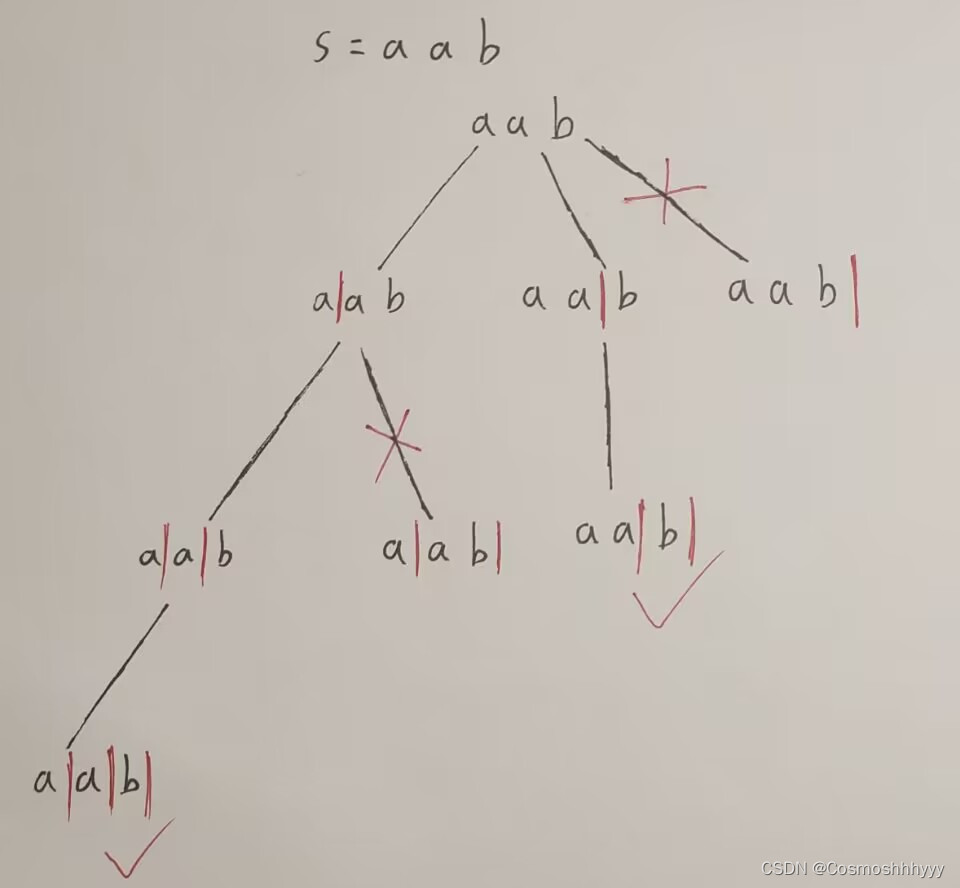
其他就和一般回溯没什么区别了,这里我也画了一个图来便于大家理解,如下: