Python使用K-means聚类分析
文章目录
- Python使用K-means聚类分析
- 介绍
- 1.集群标签作为特征
- 一、k-均值聚类
- 二、示例 - 加州住房
- 2.KMeans
- 总结
介绍
提示：这里可以添加本文要记录的大概内容：
本文将使用所谓的无监督学习算法。 无监督算法不使用目标； 相反，它们的目的是学习数据的某些属性，以某种方式表示特征的结构。 在用于预测的特征工程的上下文中，您可以将无监督算法视为一种“特征发现”技术。
聚类只是意味着根据点之间的相似程度将数据点分配给组。 可以说，聚类算法使“物以类聚”。
当用于特征工程时，我们可以尝试发现代表细分市场或具有相似天气模式的地理区域的客户群。 添加集群标签的功能可以帮助机器学习模型理清复杂的空间或邻近关系。
1.集群标签作为特征
应用于单个实值特征，聚类就像传统的“分箱”或“离散化”变换。 在多个特征上，它就像“多维合并”（有时称为矢量量化）。
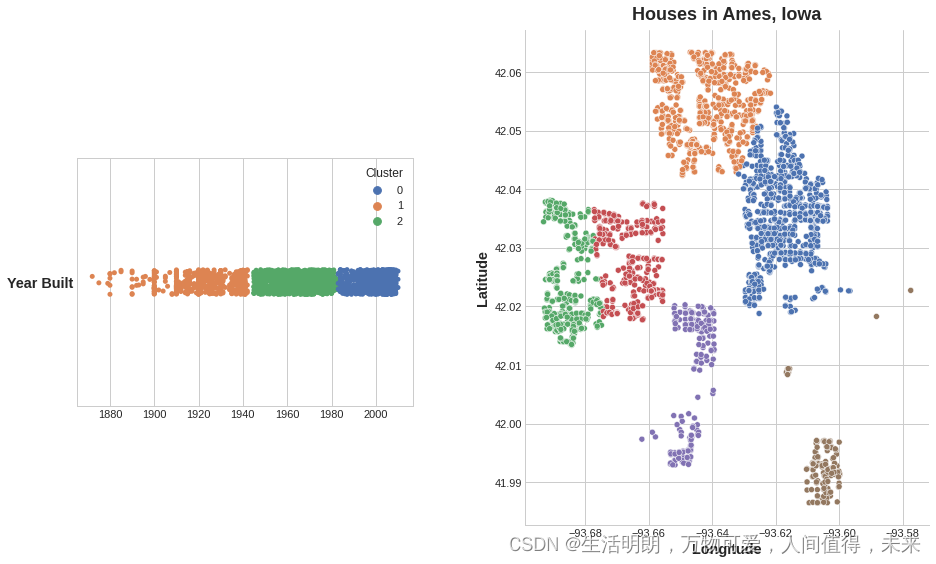添加到数据框，集群标签的功能可能如下所示：
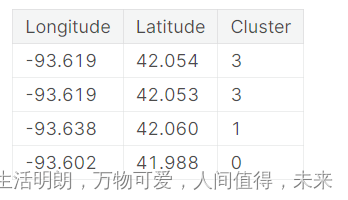
请务必记住，此聚类功能是分类的。 在这里，它显示为典型的聚类算法会产生的标签编码（即，作为整数序列）； 根据您的模型，单热编码可能更合适。添加聚类标签的动机是聚类会将特征之间的复杂关系分解为更简单的块。 然后，我们的模型可以一个接一个地学习更简单的块，而不必一次学习所有复杂的整体。 这是一种“分而治之”的策略。
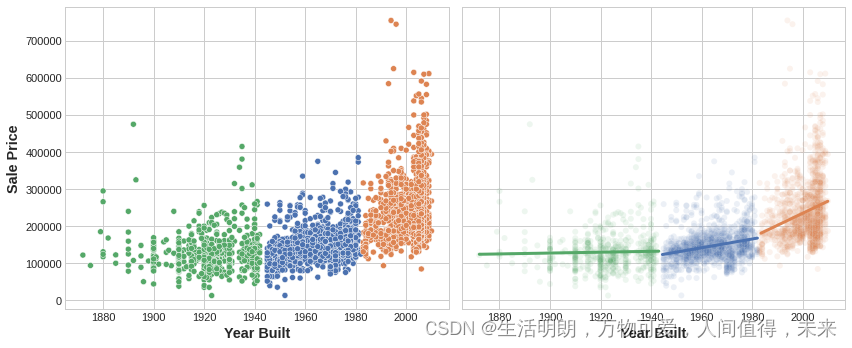
该图显示了聚类如何改进简单的线性模型。 YearBuilt 和 SalePrice 之间的曲线关系对于这种模型来说太复杂了——它欠拟合。 然而，在较小的块上，这种关系几乎是线性的，并且模型可以轻松学习。
提示：以下是本篇文章正文内容，下面案例可供参考
一、k-均值聚类
有很多聚类算法。 它们的主要区别在于如何衡量“相似性”或“接近性”，以及它们使用的特征类型。 我们将使用的算法 k-means 直观且易于在特征工程环境中应用。 根据您的应用程序，另一种算法可能更合适。
K 均值聚类使用普通直线距离（换言之，欧几里德距离）来衡量相似性。 它通过在特征空间内放置一些称为质心的点来创建聚类。 数据集中的每个点都分配给它最接近的质心的集群。 “k-means”中的“k”是它创建的质心（即簇）的数量。 您自己定义 k。
您可以想象每个质心通过一系列辐射圆捕获点。 当来自竞争质心的多组圆圈重叠时，它们会形成一条线。 结果就是所谓的 Voronoi 镶嵌。 曲面细分向您展示了未来数据将被分配到哪些集群； 曲面细分本质上是 k-means 从其训练数据中学到的东西。
上述 Ames 数据集上的聚类是 k 均值聚类。 这是同一张图，显示了曲面细分和质心。
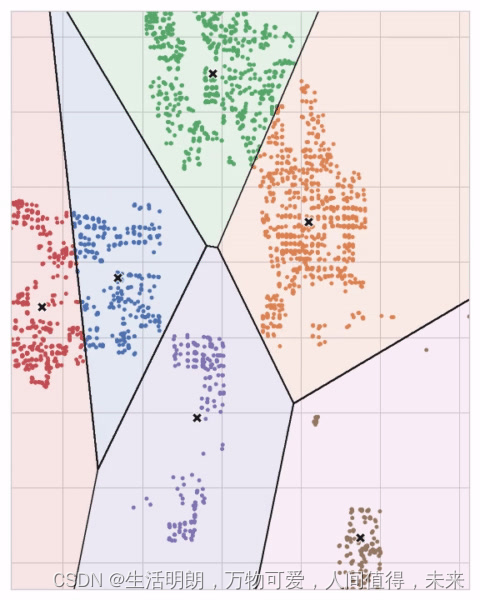
让我们回顾一下 k-means 算法如何学习聚类以及这对特征工程意味着什么。 我们将重点关注 scikit-learn 实现中的三个参数：n_clusters、max_iter 和 n_init。
这是一个简单的两步过程。 该算法首先随机初始化一些预定义数量 (n_clusters) 的质心。 然后迭代这两个操作：
将点分配给最近的簇质心
移动每个质心以最小化到其点的距离
它迭代这两个步骤，直到质心不再移动，或者直到达到某个最大迭代次数 (max_iter)。
质心的初始随机位置经常会以较差的聚类结束。 由于这个原因，该算法重复多次（n_init）并返回每个点与其质心之间的总距离最小的聚类，即最佳聚类。
下面的动画显示了正在运行的算法。 它说明了结果对初始质心的依赖性以及迭代直到收敛的重要性。
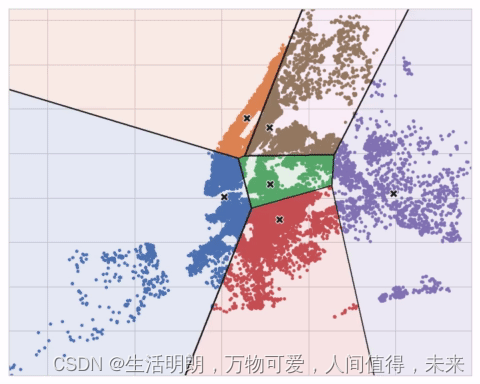
您可能需要为大量集群增加 max_iter 或为复杂数据集增加 n_init。 通常，您需要自己选择的唯一参数是 n_clusters（即 k）。 一组特征的最佳划分取决于您使用的模型和您试图预测的内容，因此最好像任何超参数一样调整它（例如通过交叉验证）。
二、示例 - 加州住房
作为空间特征，California Housing 的“纬度”和“经度”自然成为 k-means 聚类的候选对象。 在此示例中，我们将这些与“MedInc”（收入中位数）进行聚类，以创建加利福尼亚不同地区的经济细分。
代码如下（示例）：
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
df = pd.read_csv("../input/fe-course-data/housing.csv")
X = df.loc[:, ["MedInc", "Latitude", "Longitude"]]
X.head()
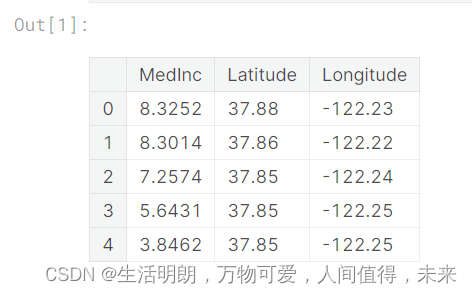
2.KMeans
由于 k 均值聚类对尺度敏感，因此使用极值重新尺度或规范化数据可能是个好主意。 我们的功能已经大致处于相同的规模，所以我们将保持原样
# Create cluster feature
kmeans = KMeans(n_clusters=6)
X["Cluster"] = kmeans.fit_predict(X)
X["Cluster"] = X["Cluster"].astype("category")
X.head()
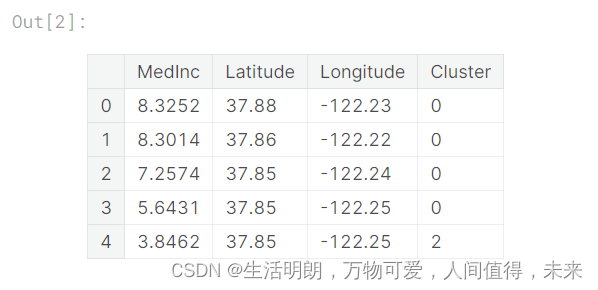
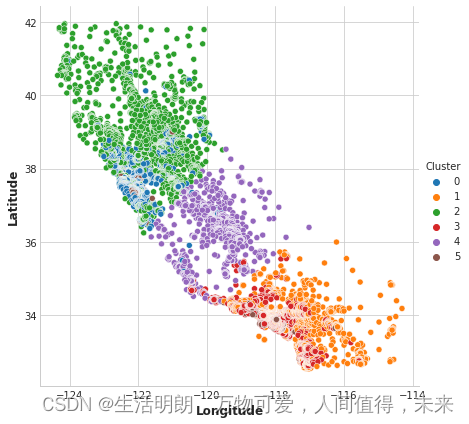
现在让我们看几幅图，看看它的效果如何。 首先，显示集群地理分布的散点图。 该算法似乎为沿海的高收入地区创建了单独的细分市场。
sns.relplot(
x="Longitude", y="Latitude", hue="Cluster", data=X, height=6,
);
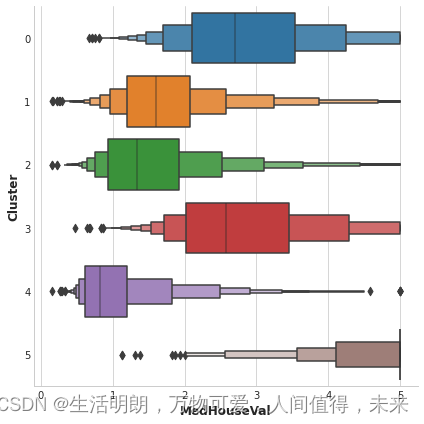
此数据集中的目标是 MedHouseVal（房屋中值）。 这些箱线图显示了目标在每个集群中的分布。 如果聚类提供信息，这些分布在大多数情况下应该在 MedHouseVal 中分离，这确实是我们所看到的。
X["MedHouseVal"] = df["MedHouseVal"]
sns.catplot(x="MedHouseVal", y="Cluster", data=X, kind="boxen", height=6);
总结
提示：这里对文章进行总结：
以上就是今天要讲的内容
