目录链接：

力扣编程题-解法汇总_分享+记录-CSDN博客

GitHub同步刷题项目：

https://github.com/September26/java-algorithms

原题链接：力扣

描述：

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

• 路径途经的所有单元格都的值都是 0 。
• 路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。

畅通路径的长度 是该路径途经的单元格总数。

示例 1：

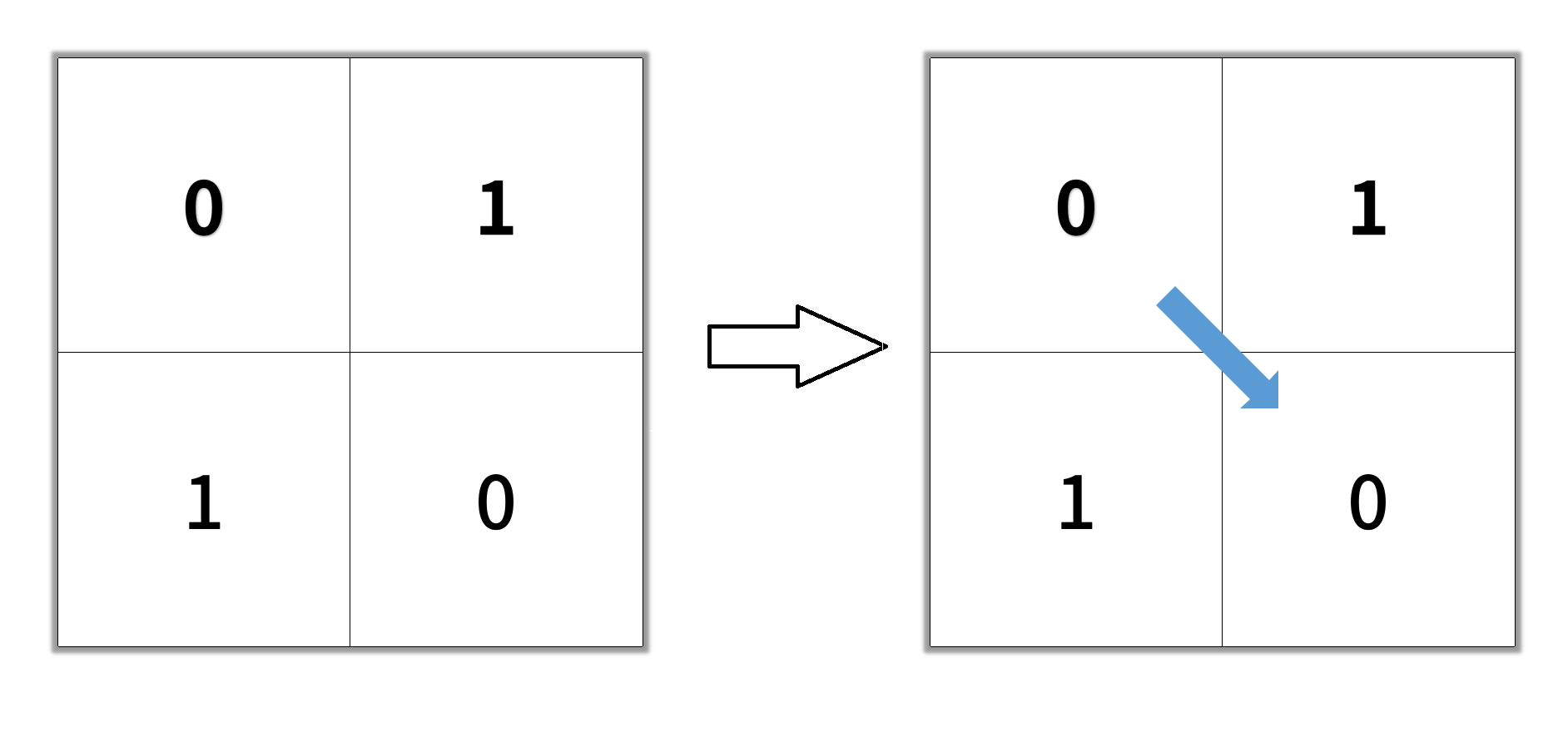
输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

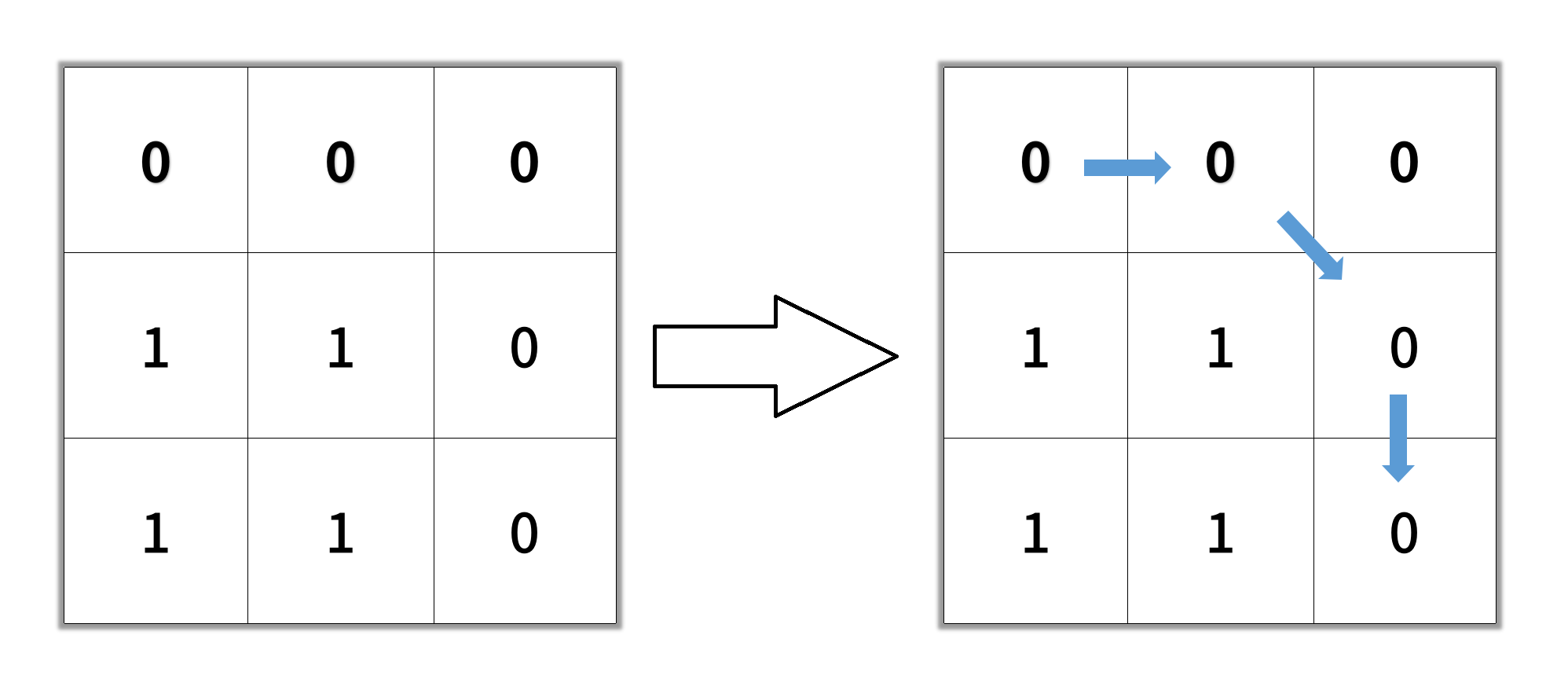
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] 为 0 或 1

解题思路：

* 解题思路：
* 从尾节点开始，先找到所有走一步可以达到的节点，放入集合list。
* 然后在从list集合中的节点触发，找到所有可能达到的节点，这些节点就是2步可以达到的，就这样遍历下去。
* 最终遍历到头节点时，流程结束。

代码：

#include <iostream>
#include <map>
#include <list>
#include <vector>
#include <map>
#include "Solution1091.h"

using namespace std;
vector<vector<int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}, {-1, 1}, {1, 1}, {1, -1}, {-1, -1}};

int searchGrid(vector<vector<int>> &from, vector<vector<int>> &grid, int step)
{
    vector<vector<int>> to;
    for (vector<int> node : from)
    {
        int y = node[0];
        int x = node[1];
        for (vector<int> direction : directions)
        {
            int newX = x + direction[1];
            int newY = y + direction[0];
            if (newX < 0 || newY < 0 || newX >= grid[0].size() || newY >= grid.size())
            {
                continue;
            }
            if (grid[newY][newX] != 0)
            {
                continue;
            }
            if (newY == 0 && newX == 0)
            {
                return step;
            }
            grid[newY][newX] = step;
            to.push_back(vector<int>{newY, newX});
        }
    }
    if (to.size() == 0)
    {
        return 1;
    }
    return searchGrid(to, grid, step - 1);
}

int Solution1091::shortestPathBinaryMatrix(vector<vector<int>> &grid)
{
    if (grid[0][0] == 1 || grid[grid.size() - 1][grid[0].size() - 1] == 1)
    {
        return -1;
    }
    if (grid.size() == 1 && grid[0].size() == 1)
    {
        return 1;
    }
    vector<vector<int>> from;
    int gridSizeY = grid.size() - 1;
    int gridSizeX = grid[0].size() - 1;
    from.push_back(vector<int>{gridSizeY, gridSizeX});
    int i = searchGrid(from, grid, -1);
    if (i == 1)
    {
        return -1;
    }
    return i * -1 + 1;
}