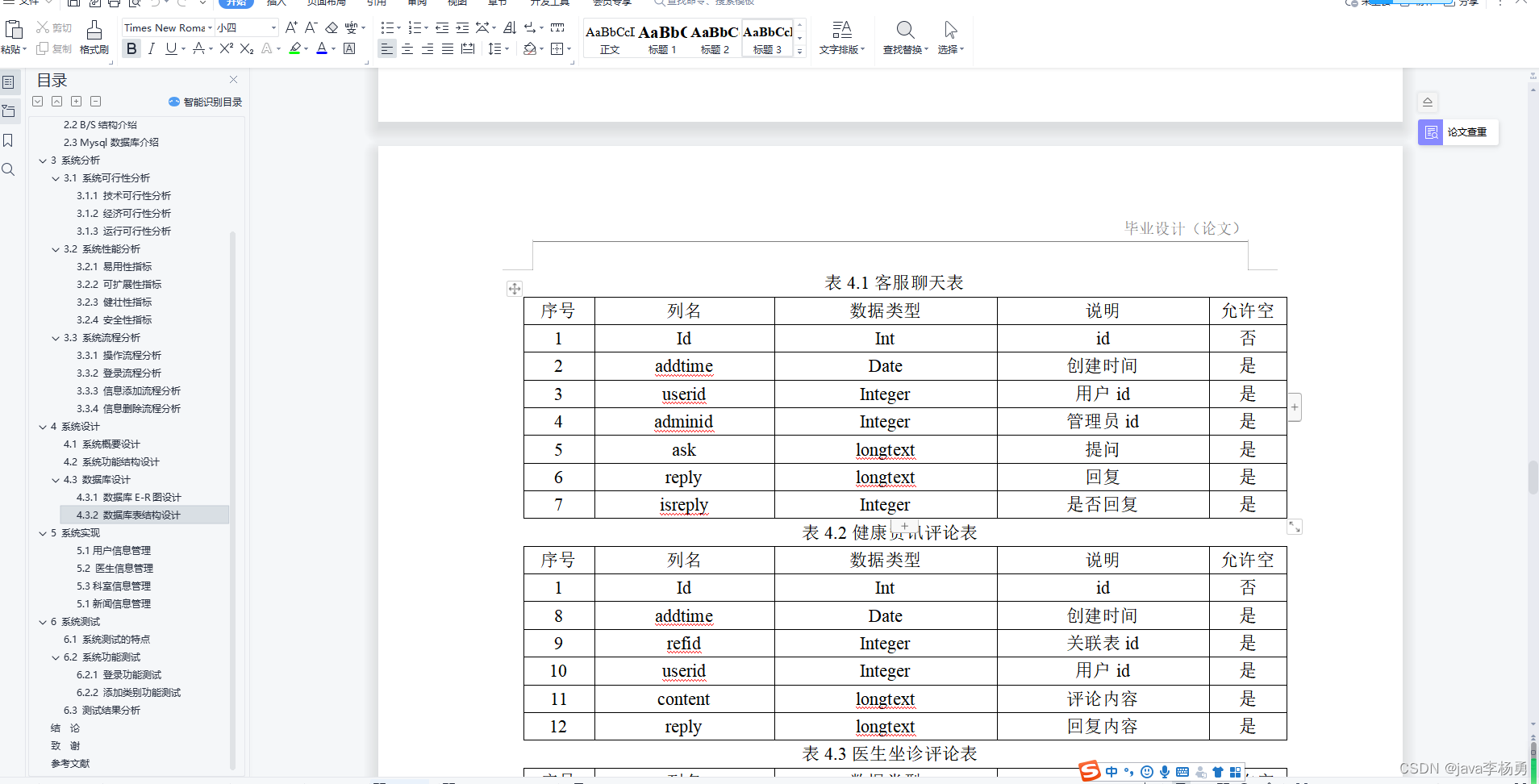
在前一节内容中,我们学习了二维匀加速运动目标的卡尔曼滤波问题,同时利用MATLAB进行了仿真验证,今天我们继续往下扩展一个维度,学习三维空间下的卡尔曼滤波问题。
话不多说,开整!!!
状态方程
既然目标是在三维空间中做匀加速运动,那么自然其在x、y、z三个方向上均会产生位移和速度,并且每个方向都有着加速度,因此,根据运动学公式,其各个方向的位置、速度、加速度可由下式得出:
x
k
=
x
k
−
1
+
x
˙
k
−
1
Δ
t
+
1
2
x
¨
k
−
1
Δ
t
2
(
1
)
x_{k} =x_{k-1}+\dot{x}_{k-1}\Delta t+\frac{1}{2}\ddot{x}_{k-1}\Delta t^2 \quad(1)
xk=xk−1+x˙k−1Δt+21x¨k−1Δt2(1)
x
˙
k
=
x
˙
k
−
1
+
x
¨
k
−
1
Δ
t
(
2
)
\dot{x}_{k}=\dot{x}_{k-1}+\ddot{x}_{k-1}\Delta t\quad(2)
x˙k=x˙k−1+x¨k−1Δt(2)
x
¨
k
=
x
¨
k
−
1
(
3
)
\ddot x_{k}=\ddot x_{k-1}\quad(3)
x¨k=x¨k−1(3)
y
k
=
y
k
−
1
+
y
˙
k
−
1
Δ
t
+
1
2
y
¨
k
−
1
Δ
t
2
(
4
)
y_{k} =y_{k-1}+\dot{y}_{k-1}\Delta t+\frac{1}{2}\ddot{y}_{k-1}\Delta t^2 \quad(4)
yk=yk−1+y˙k−1Δt+21y¨k−1Δt2(4)
y
˙
k
=
y
˙
k
−
1
+
y
¨
k
−
1
Δ
t
(
5
)
\dot{y}_{k}=\dot{y}_{k-1}+\ddot{y}_{k-1}\Delta t\quad(5)
y˙k=y˙k−1+y¨k−1Δt(5)
y
¨
k
=
y
¨
k
−
1
(
6
)
\ddot y_{k}=\ddot y_{k-1}\quad(6)
y¨k=y¨k−1(6)
z
k
=
z
k
−
1
+
z
˙
k
−
1
Δ
t
+
1
2
z
¨
k
−
1
Δ
t
2
(
7
)
z_{k} =z_{k-1}+\dot{z}_{k-1}\Delta t+\frac{1}{2}\ddot{z}_{k-1}\Delta t^2 \quad(7)
zk=zk−1+z˙k−1Δt+21z¨k−1Δt2(7)
z
˙
k
=
z
˙
k
−
1
+
z
¨
k
−
1
Δ
t
(
8
)
\dot{z}_{k}=\dot{z}_{k-1}+\ddot{z}_{k-1}\Delta t\quad(8)
z˙k=z˙k−1+z¨k−1Δt(8)
z
¨
k
=
z
¨
k
−
1
(
9
)
\ddot z_{k}=\ddot z_{k-1}\quad(9)
z¨k=z¨k−1(9)
其中:
x
k
x_k
xk:目标在k时刻的x方向的位置;
x
˙
k
\dot{x}_k
x˙k:目标在k时刻的x方向的速度;
x
¨
k
\ddot{x}_k
x¨k:目标在k时刻的x方向的加速度;
x
k
−
1
x_{k-1}
xk−1:目标在k-1时刻的x方向的位置;
x
˙
k
−
1
\dot{x}_{k-1}
x˙k−1:目标在k-1时刻的x方向的速度;
x
¨
k
−
1
\ddot{x}_{k-1}
x¨k−1:目标在k-1时刻的x方向的加速度
y、z方向的各参数意义同上,不再叙述。
那么此时的目标状态可以表示为:
X
k
=
[
x
k
x
˙
k
x
¨
k
y
k
y
˙
k
y
¨
k
z
k
z
˙
k
z
¨
k
]
X_k = [x_k \quad \dot x_k \quad \ddot x_k\quad y_k \quad \dot y_k \quad \ddot y_k \quad z_k \quad \dot z_k \quad \ddot z_k]
Xk=[xkx˙kx¨kyky˙ky¨kzkz˙kz¨k]
考虑目标在运动过程中的过程噪声
V
k
V_k
Vk的影响,将式(1)~(9)写为矩阵相乘形式,则可以表示下式:
X
k
=
[
1
Δ
t
1
2
Δ
t
2
0
0
0
0
0
0
0
1
Δ
t
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
Δ
t
1
2
Δ
t
2
0
0
0
0
0
0
0
1
Δ
t
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
Δ
t
1
2
Δ
t
2
0
0
0
0
0
0
0
1
Δ
t
0
0
0
0
0
0
0
0
1
]
X
k
−
1
+
V
k
=
F
X
k
−
1
+
V
k
X_{k} = \begin{bmatrix}1&\Delta t&\frac{1}{2}\Delta t^2&0&0&0&0&0&0\\[0.3em]0&1&\Delta t&0&0&0&0&0&0\\[0.3em]0&0&1&0&0&0&0&0&0\\[0.3em]0&0&0&1&\Delta t&\frac{1}{2}\Delta t^2&0&0&0\\[0.3em]0&0&0&0&1&\Delta t&0&0&0\\[0.3em]0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&1&\Delta t&\frac{1}{2}\Delta t^2\\0&0&0&0&0&0&0&1&\Delta t\\0&0&0&0&0&0&0&0&1\end{bmatrix}X_{k-1} + V_k = FX_{k-1} +V_k
Xk=
100000000Δt1000000021Δt2Δt1000000000100000000Δt1000000021Δt2Δt1000000000100000000Δt1000000021Δt2Δt1
Xk−1+Vk=FXk−1+Vk
至此,目标的状态方程便已介绍完成,其中F称为状态转移矩阵,下面介绍观测方程。
观测方程
同样,观测方程仍然是雷达测量过程的假设,那么在三维空间的背景下,此时的测量值
Z
k
Z_k
Zk就是三个方向的位置信息也即:
Z
k
=
[
z
x
z
y
z
z
]
Z_k = [z_x \quad z_y\quad z_z]
Zk=[zxzyzz]
量测值与真实值的关系即可以通过观测方程进行描述,考虑量测过程中的不确定性即量测噪声
R
k
R_k
Rk如下式:
Z
k
=
[
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
]
X
k
+
W
k
=
H
X
k
+
W
k
\begin{aligned} \\ Z_k&& =\begin{bmatrix}1&0&0&0&0&0&0&0&0\\ 0&0&0&1&0&0&0&0&0\\0&0&0&0&0&0&1&0&0\end{bmatrix}X_k+W_k=H X_k+W_k \end{aligned}
Zk=
100000000010000000001000000
Xk+Wk=HXk+Wk
至此,量测方程也介绍完毕,下面进行仿真测试。
MATLAB仿真
在对二维匀加速运动目标建模完成后,即可对其进行MATLAB仿真,仿真背景如下:
- 采样点数:200
- 采样时间:0.1s
- 初始位置:[7 11 21]
- 初始速度:[10 20 15]
- 初始加速度:[0.5 1 0.75]
- 过程噪声方差:1e-6
- 量测噪声方差:100
下面对其进行仿真,其中:
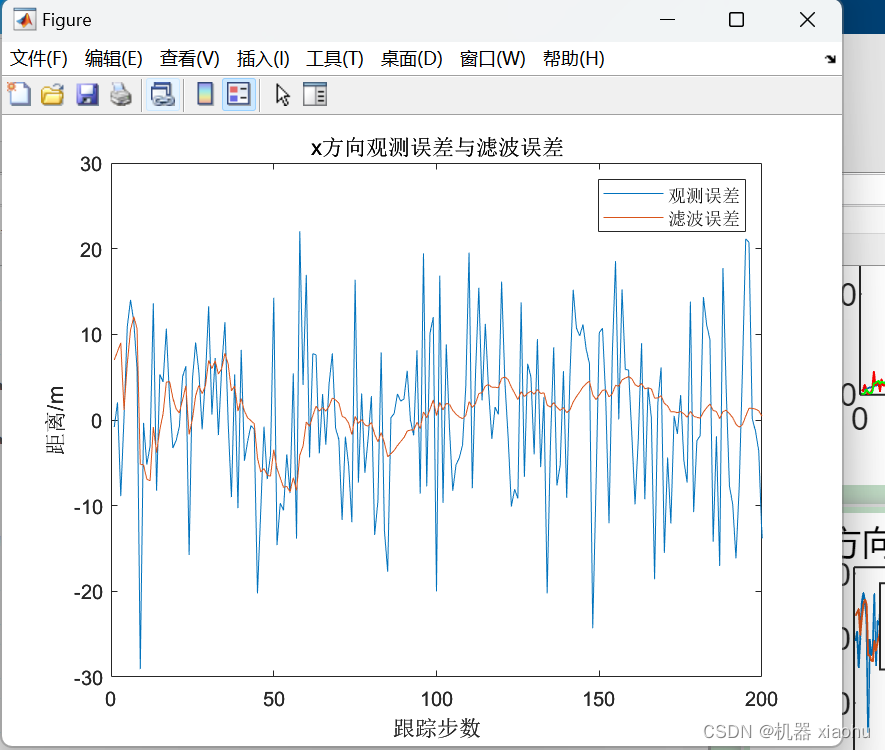
> 观测误差 = 观测值 - 真实值
> 滤波误差 = 滤波值 - 真实值
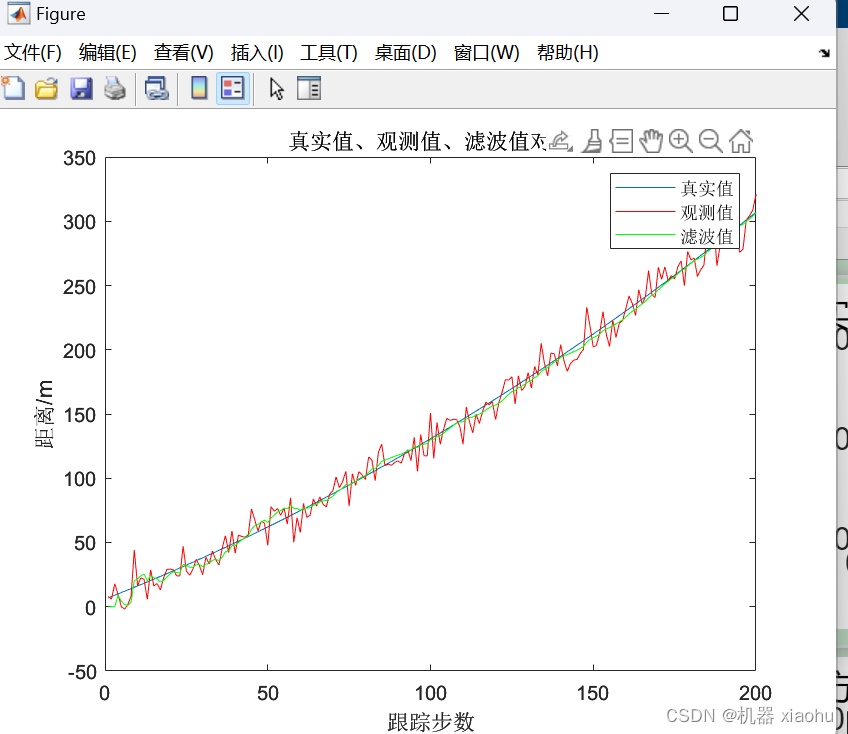
x方向的位置滤波效果对比
x方向的距离滤波误差对比
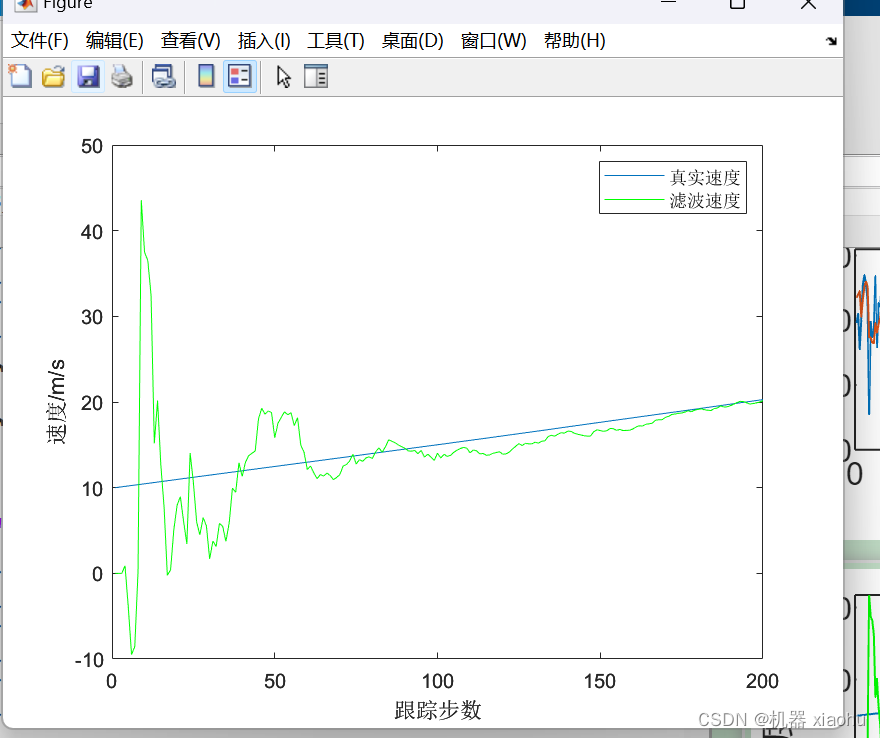
x方向的速度滤波效果对比
x方向的速度滤波误差对比

x方向的加速度滤波效果
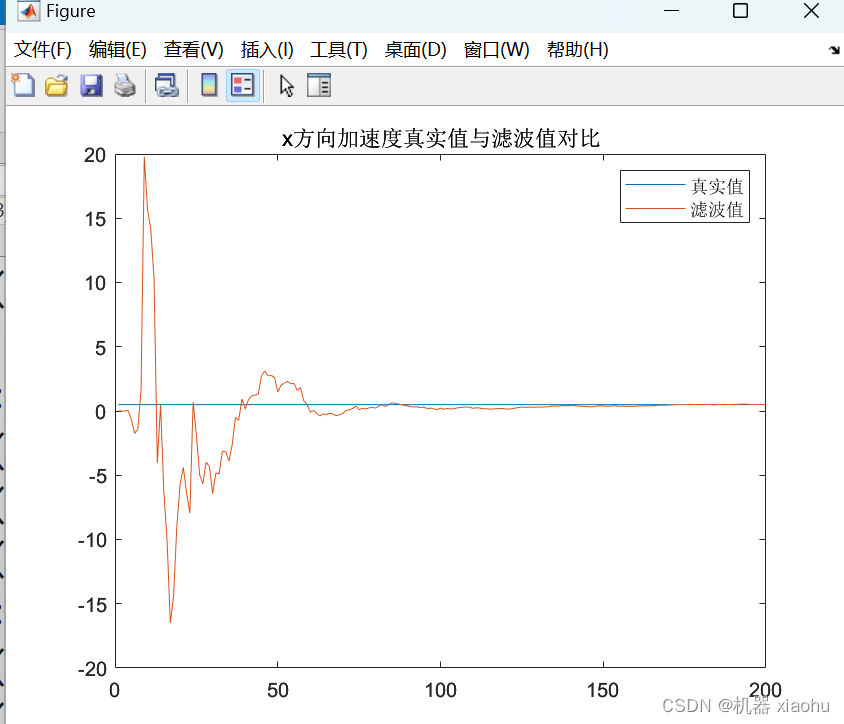
其余两个方向的滤波效果不在此处进行展示,从效果中我们发现,随着跟踪时间的递进,滤波的效果明显越来越好。
上述内容即使今天的全部内容了,感谢大家的观看。
如果方便,辛苦大家点个赞和关注哦!
您的点赞或评论或关注是对我最大的肯定,谢谢大家!!!