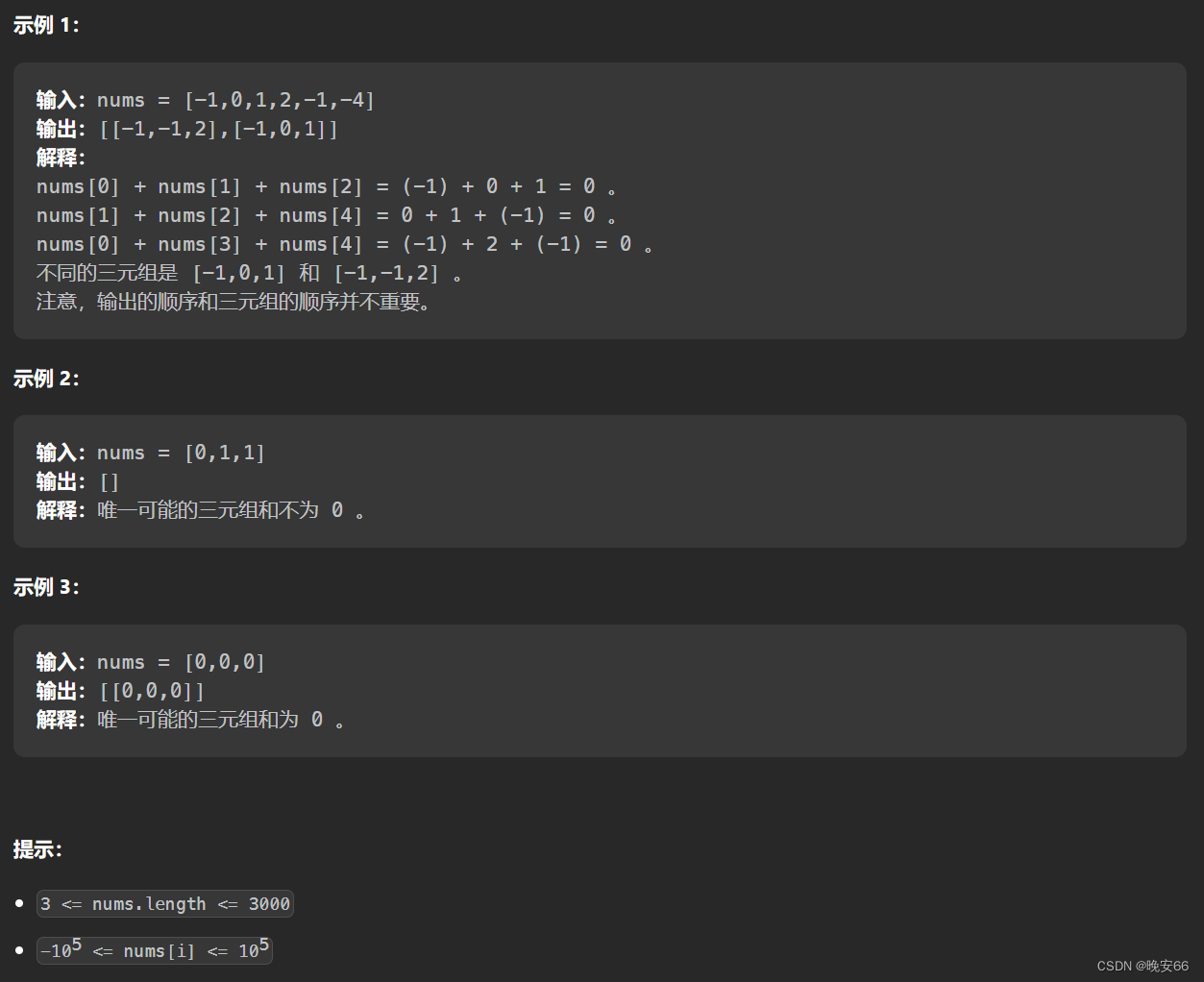
目录
前言:
104. 二叉树的最大深度 - 力扣(LeetCode)
111. 二叉树的最小深度 - 力扣(LeetCode)
前序遍历:
后序遍历:
总结:
前言:
今天还是对树的基础题进行刷题,感兴趣的同学可以看一看。
104. 二叉树的最大深度 - 力扣(LeetCode)
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
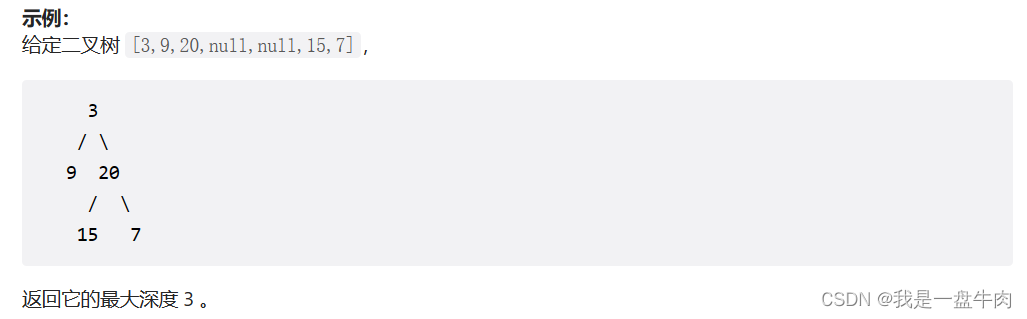
注意点:深度不是高度,我们用图片给大家演示: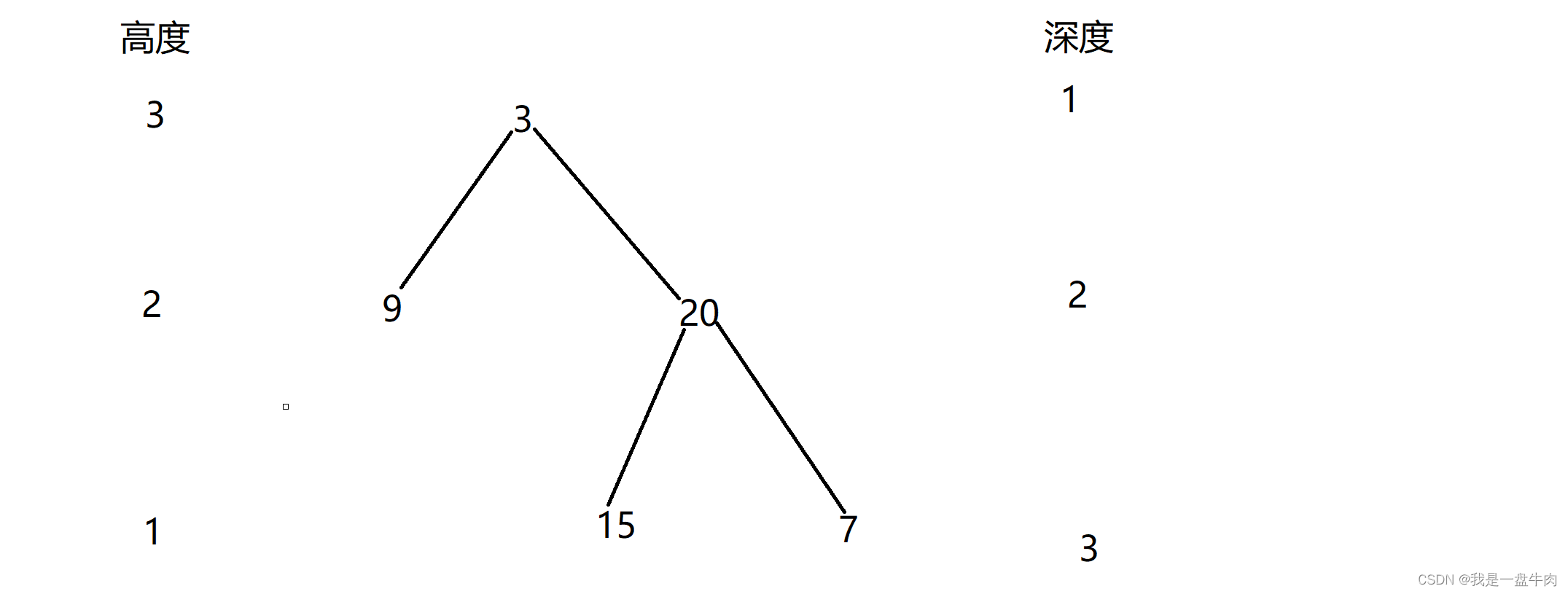
深度:指该节点到根节点的距离。
高度:指节点到叶子节点的距离。
其实我们简单的推一下就可以知道用什么查找方式来对二叉树的深度和高度进行查找
求节点深度:
在二叉树中,求深度通常需要遍历树上的每一个节点,并记录每一个节点的深度。根据深度优先遍历 (DFS) 的思想,我们可以使用后序遍历来求深度。
后序遍历的遍历顺序是:先遍历左子树,再遍历右子树,最后遍历根节点。因此,当我们遍历到某个节点时,它的左子树和右子树都已经被处理过了,我们可以根据它的左子树和右子树的深度来求出该节点的深度。然后再将该节点的深度加 1,就可以得到它的父节点的深度。
使用后序遍历求深度的好处在于,我们可以在遍历过程中利用子问题的结果,从底层向上层逐步推导,避免了反复遍历子树的过程,从而提高了遍历效率。此外,该算法的空间复杂度为 O(1),相比于其他遍历方式,它不需要使用额外的存储空间,较为节省空间。
求节点高度:
在二叉树中,求深度时可以使用前序遍历的方式进行递归求解。前序遍历的遍历顺序是:先遍历根节点,然后遍历左子树,最后遍历右子树。因此,当我们遍历到某个节点时,该节点的深度已经确定,可以根据该节点的深度,推算出其子节点的深度并记录下来。接着,我们可以递归遍历该节点的左子树和右子树,分别计算左右子树的深度,并将两者中较大的深度作为该节点的深度。这样,我们依次遍历每个节点,就可以得到该树的深度。
使用前序遍历求深度的好处在于,我们可以在遍历过程中,自下而上地递推推算深度。在处理子问题时,如果子问题的深度已知,就可以利用已知的深度求解当前节点的深度。这样可以避免重复遍历子树,从而提高求解效率。
求二叉树的最大深度,实际上就是在求这个二叉树的根节点的高度。
class Solution {
public:
int getdepth(TreeNode* node) {
if (node == NULL) return 0;
int leftdepth = getdepth(node->left); // 左
int rightdepth = getdepth(node->right); // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;
}
int maxDepth(TreeNode* root) {
return getdepth(root);
}
};111. 二叉树的最小深度 - 力扣(LeetCode)
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。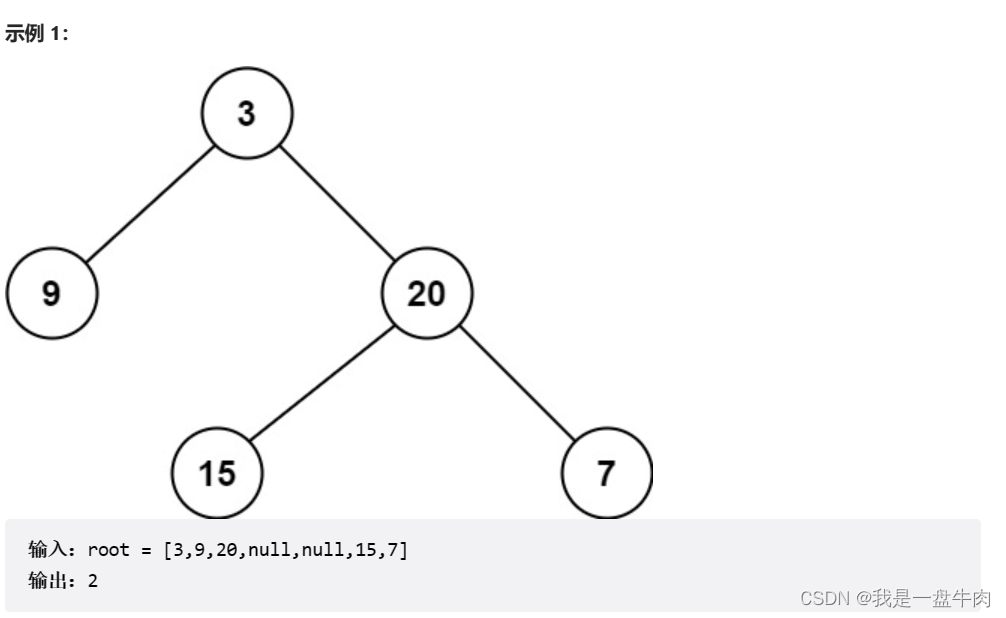
其实这道题虽然部分思路是和求最大深度一样的,但是还是有很多的细节不一致,因此我们不可以直接套用二叉树 最大深度进行计算。很多人就是对这里的最小深度理解错误才导致解题出错
叶子节点:
在二叉树中,叶子节点指的是没有子节点的节点,也称为终端节点。二叉树中只有叶子节点才是最底层的节点,其余的节点都有至少一个子节点。
前序遍历:
具体做法如下:
如果根节点为空,则返回 0。
如果根节点的左子树为空,则递归计算右子树的最小深度,并将其加 1,即为整棵树的最小深度。
如果根节点的右子树为空,则递归计算左子树的最小深度,并将其加 1,即为整棵树的最小深度。
如果根节点的左右子树均非空,则递归计算左子树和右子树的最小深度,将两者中较小的深度加 1,即为整棵树的最小深度。
class Solution {
public:
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
// 中
// 当一个左子树为空,右不为空,这时并不是最低点
if (node->left == NULL && node->right != NULL) {
return 1 + rightDepth;
}
// 当一个右子树为空,左不为空,这时并不是最低点
if (node->left != NULL && node->right == NULL) {
return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
}
int minDepth(TreeNode* root) {
return getDepth(root);
}
};后序遍历:
具体做法如下:
如果根节点为空,则返回 0。
如果根节点的左子树和右子树均为空,返回 1。
如果根节点的左子树或右子树为空,则递归计算另一棵子树的最小深度,并将其加 1,即为整棵树的最小深度。
如果根节点的左右子树均非空,则递归计算左子树和右子树的最小深度,将两者中较小的深度加 1,即为整棵树的最小深度。
def min_depth(root):
if root is None:
return 0
if root.left is None and root.right is None:
return 1
if root.left is None:
return min_depth(root.right) + 1
if root.right is None:
return min_depth(root.left) + 1
return min(min_depth(root.left), min_depth(root.right)) + 1总结:
二叉树章节是递归的重灾区,各位要想学好二叉树,就要学好递归。
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力!