| 一、实验目的: 理解并掌握回溯法与分支限界法的联系与区别,学会构造不同问题的解空间树,用上述两种算法解决装载问题。 | ||||||||
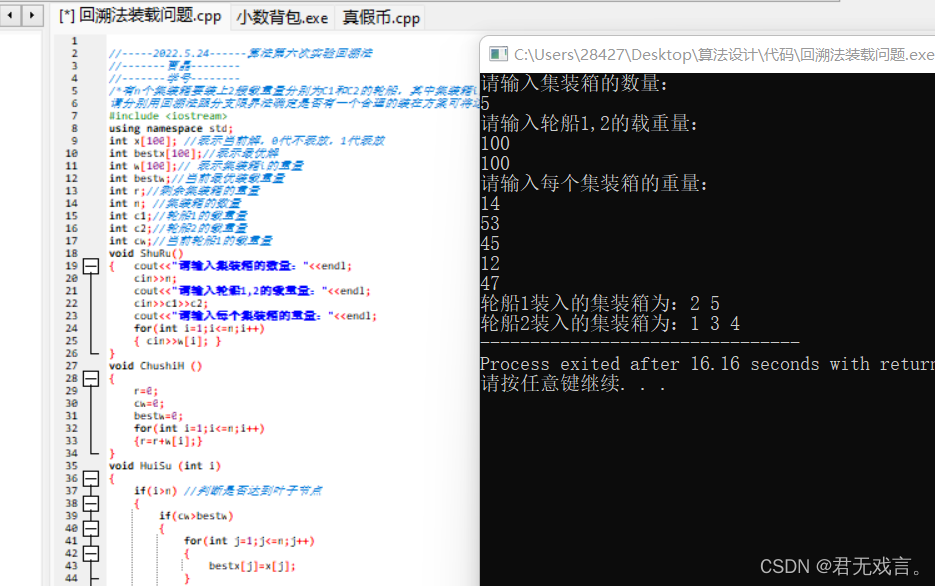
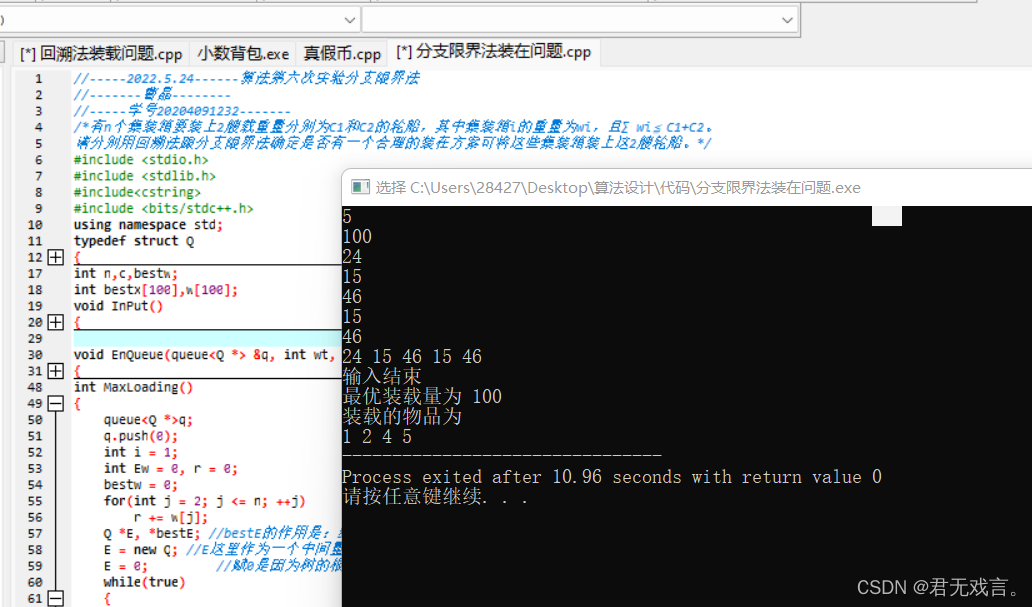
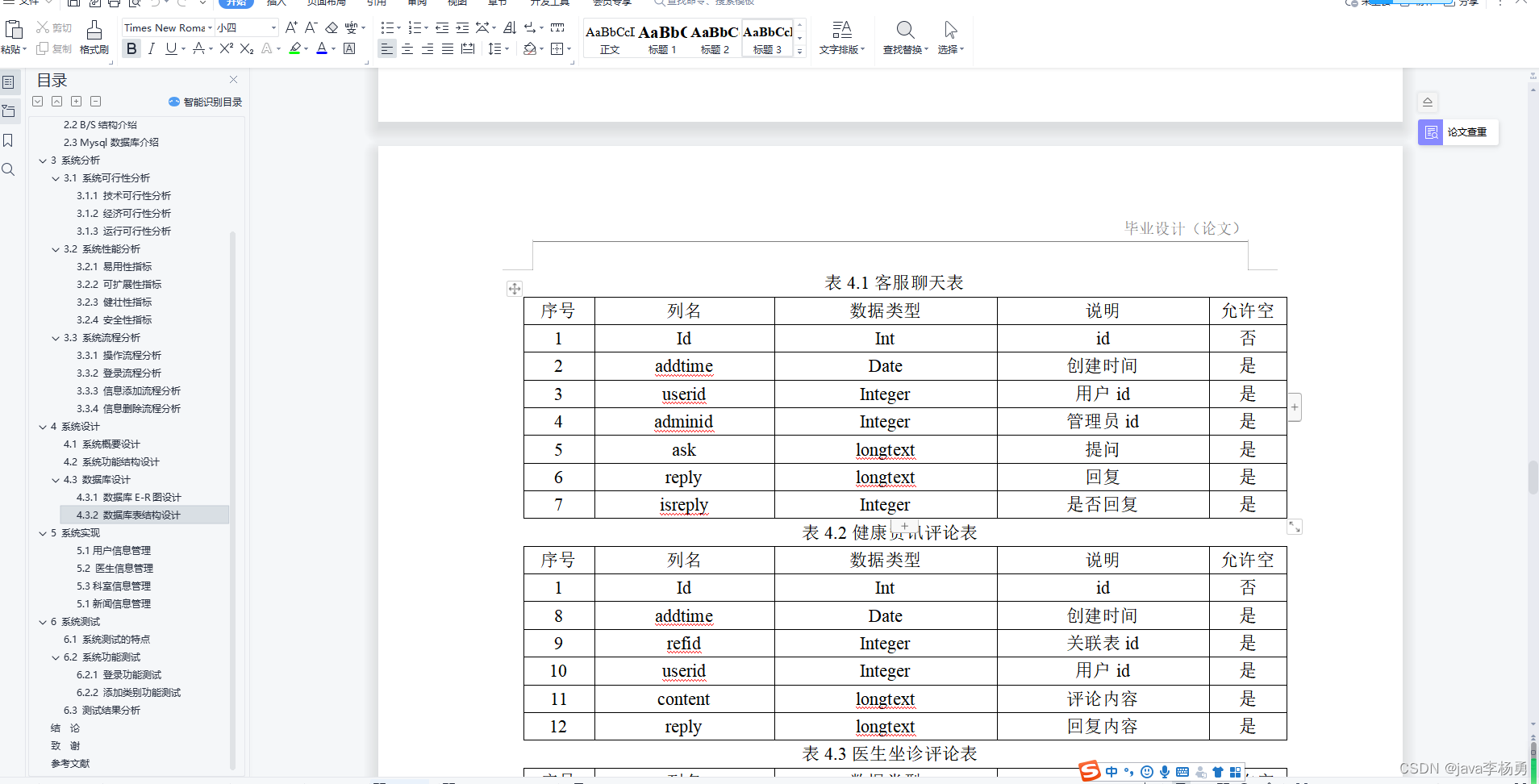
问题描述:有n个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集装箱i的重量为wi,且∑wi≦C1+C2。请分别用回溯法跟分支限界法确定是否有一个合理的装在方案可将这些集装箱装上这2艘轮船。 输入:多组测试数据。每组测试数据包括两行:第一行输入集装箱数目n(n<1000),以及两艘轮船的载重C1和C2;第二行输入n个整数,表示每个集装箱的重量。 输出:如果存在合理装载方案,输出第一艘轮船的最大装载重量;否则输出“NO”。 程序代码:(不允许粘图,重点语句加上注释) 回溯法: #include <iostream> using namespace std; int x[100]; int bestx[100]; int w[100]; int bestw; int r,n,c1,c2,cw; void ShuRu() { cout<<"请输入集装箱的数量:"<<endl; cin>>n; cout<<"请输入轮船1,2的载重量:"<<endl; cin>>c1>>c2; cout<<"请输入每个集装箱的重量:"<<endl; for(int i=1;i<=n;i++) { cin>>w[i]; } } void ChushiH () { r=0; cw=0; bestw=0; for(int i=1;i<=n;i++) {r=r+w[i];} } void HuiSu (int i) { if(i>n) //判断是否达到叶子节点 { if(cw>bestw) { for(int j=1;j<=n;j++) { bestx[j]=x[j]; } bestw=cw; } } r=r-w[i]; if(cw+w[i]<=c1) //判断该集装箱到底放不放 { x[i]=1; cw=cw+w[i]; HuiSu(i+1); //当节点i的子树延伸结束时要返回i节点 x[i]=0; cw=cw-w[i]; } if(cw+r>bestw) //判断先不放该集装箱后是否还有可行解 { x[i]=0; HuiSu(i+1); } r=r+w[i];//当节点i的子树延伸结束时要返回i节点 } void ShuChu () {int i; int c2w=0; for(int i=1;i<=n;i++) { if(bestx[i]==0) { c2w=c2w+w[i]; } } if(c2w>c2) cout<<"装不下啊!"<<endl; else { cout<<"轮船1装入的集装箱为:"; for( i=1;i<=n;i++) { if(bestx[i]==1) cout<<i<<" "; } cout<<endl; cout<<"轮船2装入的集装箱为:"; for(i=1;i<=n;i++) { if(bestx[i]!=1) cout<<i<<" "; } } } int main() { ShuRu(); ChushiH(); HuiSu(1); ShuChu(); return 0; } 分支限界法: #include <stdio.h> #include <stdlib.h> #include<cstring> #include <bits/stdc++.h> using namespace std; typedef struct Q { Q *parent; int lchild; int weight; }Q; int n,c,bestw; int bestx[100],w[100]; void InPut() { scanf("%d %d", &n, &c); for(int i = 1; i <= n; ++i) scanf("%d", &w[i]); for(int i = 1; i <= n; ++i) printf("%d ", w[i]); cout << endl; printf("输入结束\n"); } //Q *&bestE 的原因是 首先bestE是个地址, 其次引用为了赋值使用, 后边for循环中用到 void EnQueue(queue<Q *> &q, int wt, int i, Q *E, Q *&bestE, int ch) { if(i == n) { if(wt == bestw) { bestE = E; bestx[n] = ch; return; } } Q *b; b = new Q; b->weight = wt; b->lchild = ch; b->parent = E; q.push(b); } int MaxLoading() { queue<Q *>q; q.push(0); int i = 1; int Ew = 0, r = 0; bestw = 0; for(int j = 2; j <= n; ++j) r += w[j]; Q *E, *bestE; //bestE的作用是:结束while循环后,bestE指向最优解的叶子节点,然后通过bestE->parent找到装入了哪些物品。 E = new Q; //E这里作为一个中间量,连接parent和child E = 0; //赋0是因为树的根的值是0,while刚开始的时候其代表root while(true) { int wt = Ew + w[i]; if(wt <= c) { if(wt > bestw) //提前更新bestW,注意更新条件 bestw = wt; EnQueue(q, wt, i, E, bestE, 1); } if(Ew + r >= bestw) //右儿子剪枝 { EnQueue(q, Ew, i, E, bestE, 0); } E = q.front(); q.pop(); if(!E) //如果取得的数是0,代表该处理下一层 { if(q.empty()) //如果队列为空,表示该循环结束了 break; q.push(0); //如果队列中还有数据,表示循环还没结束。在该层的末尾加一个0标识符 E = q.front(); q.pop(); i++; //下一层走起 r -= w[i]; //计算剩余的重量 } Ew = E->weight; //不要忘记更新最新节点的值 } for(int j = n - 1; j > 0; --j) { bestx[j] = bestE->lchild; bestE = bestE->parent; } } void OutPut() { printf("最优装载量为 %d\n", bestw); printf("装载的物品为 \n"); for(int i = 1; i <= n; ++i) if(bestx[i] == 1) printf("%d ", i); } int main() { InPut(); MaxLoading(); OutPut(); } 程序测试及运行结果: 1.回溯法
2.分支限界法
| ||||||||
| 分析与讨论: 1.问题的思路 在问题的边带权的解空间树中进行广度优先搜索再找一个叶结点使其对应路径的权最小(最大)。当搜索到达一个扩展结点时,一次性扩展它的所有孩子然后将满足约束条件且最小耗费函数£目标函数限界的孩子,插入活结点表中最后从活结点表中取下一结点同样扩展,直到找到所需的解或活动结点表为空为止。由此可知,装载问题等价于特殊的0-1背包问题。 2.回溯法和分支限界法的不同 (1)求解目标不同 回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。 (2)搜索方式不同 回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。 其中分支限界法包括队列式(FIFO)分支限界法(即将活结点表组织成一个队列,按照先进先出(FIFO)原则选取下一个结点为扩展结点。)和优先队列式分支限界法(即将活结点表组织成一个优先队列,按照规定的优先级选取优先级最高的结点成为当前扩展结点。) |
算法程序设计 之 装载问题(6/8)
news2026/2/13 20:49:59
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/673328.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
论文浅尝 | DEER:解释实体关系的描述性知识图谱
笔记整理:王润哲,东南大学硕士,研究方向为多元关系抽取 链接:https://aclanthology.org/2022.emnlp-main.448.pdf 动机 实体关系是知识图谱中不可或缺的一层重要信息,它们描述了实体之间的语义关系,这种连接…
【力扣刷题 | 第十二天】
目录 前言:
104. 二叉树的最大深度 - 力扣(LeetCode)
111. 二叉树的最小深度 - 力扣(LeetCode)
前序遍历: 后序遍历:
总结: 前言: 今天还是对树的基础题进行刷题&am…
大数据Doris(四十七):开启Steam Load记录
文章目录
开启Steam Load记录
一、停止 Doris 集群
二、在 node3-node5 BE 节点上配置 be.conf
三、重新启动 Doris 集群 开启Steam Load记录
后续执行Stream Load 导入任务后,我们会在Doris集群中会查询对应Stream Load任务的情况,默认BE是不记录S…
【Rust日报】2023-06-20 使用Quickwit、Jaeger和Grafana监控您的Rust应用程序
使用Quickwit、Jaeger和Grafana监控您的Rust应用程序 你可能已经看过了Lucas Palmieri的博客文章Are we observable yet? An introduction to Rust telemetry。如果你还没有看过,我们建议阅读一下,因为它提供了一个全面的介绍,介绍了如何处理…
【Python 基础篇】Python 函数:代码重用的利器
文章目录 导言一、创建函数二、函数参数1、位置参数2、关键字参数3、默认参数 三、函数返回值四、函数的高级用法1、递归函数2、匿名函数3、内置函数 总结 导言
函数是一种在Python中定义和封装可重用代码的重要机制。它们使我们能够将复杂的任务分解为更小的部分,…
【算法与数据结构】15、LeetCode三数之和
文章目录 一、题目二、双指针法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、双指针法 思路分析:我们使用双指针法,但这道题因为要求数组三个元素的和,一共用到了三个指…
新人拿到一个web项目如何使用idea发布运行
本文描述的是一个新手,拿到一个web项目,使用idea如何发布运行。项目中没有非常复杂的元素,只是试着描述应该如何配置相关内容。 内容描述前提,首先请您确认tomcat已经安装,其次确认jdk已经安装,并明确他们在…
基于Java农产品仓库管理系统设计实现(源码+lw+部署文档+讲解等)
博主介绍: ✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精…
管理类联考——逻辑——技巧篇——论证推理(10-12 道左右)——五大秒杀思路
逻辑考试出题思路分类
论证推理(10-12 道左右)
论证推理细分思路
假设——补全逻辑假设——引入前提前真后假 - 前假后真建立联系型支持由果推因的削弱由因推果 / 直接引入他因指出不同 / 指出相同五大固定秒杀思路解释类题目评价类题目
论证推理题目…
C语言学习(二十四)---递归与冒泡排序法
在前面几节的内容中,我们学习了指针的相关概念,至此,指针的内容就暂时告一段落了,今天我们将继续向下学习,主要内容为递归和冒泡排序法,好了,话不多说,开整!!…
【AndroidUI设计】主界面设计-Toolbar的简单使用
文章目录 一、引言二、了解三、编码1、UI设计2、编码 一、引言
描述:需要设计一个主界面,菜单通过主界面的左边界划入,实现点击跳转修改主界面内容的一个效果,并且点击非内容区域恢复原界面的一个效果。做到菜单的弹出࿰…
Vue3 One Piece Study
目录 脚手架安装vue3
使用vue-cli创建 使用vite创建 setup
介绍
示例使用
ref函数
介绍
代码示例
reactive函数
介绍
代码示例 脚手架安装vue3
使用vue-cli创建 vue create 项目名 安装完成
进入到刚才创建的项目目录中
cd vue3_test
输入npm run serve测试 使用…
基于Java健康综合咨询问诊平台设计实现(源码+lw+部署文档+讲解等)
博主介绍: ✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精…
STM32 HAL库开发——入门篇(2):定时器
目录
一、TIMER定时器概述
1.1 软件定时原理
1.2 定时器定时原理
1.3 STM32定时器分类
1.4 STM32定时器特性表
1.5 STM32基本、通用、高级定时器功能整体的区别
二、基本定时器
2.1 基本定时器简介
2.3 STM32定时器计数模式及溢出条件
2.4 定时器中断实验相关寄存器 …
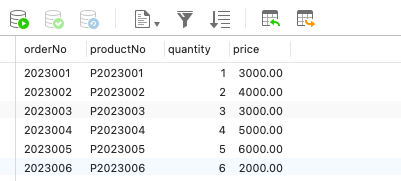
MySQL创建商品订单数据库
目录 一、商品分类表 ProductClass1. 创建 ProductClass表2. 插入数据3. 展示 二、客户表 Customer记录1. 创建 Customer表2. 插入数据3. 展示 三、商品表 Product1. 创建 Product表2. 插入数据3. 展示 四、员工表Employee1. 创建 Employee表2. 插入数据3. 展示 五、订单主表 O…
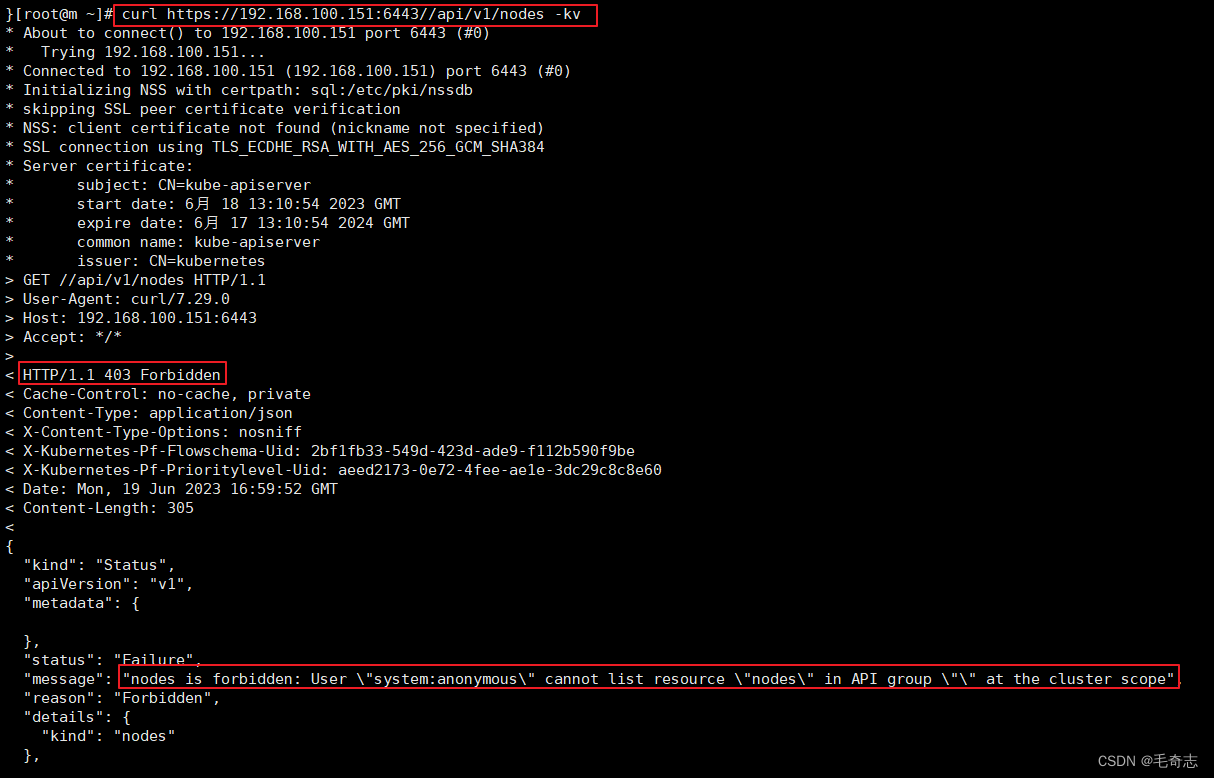
kubernetes_核心组件_KubeProxy_KubeProxy三种模式和参数解析
系列文章目录 文章目录 系列文章目录前言一、kube-proxy三种服务负载模式1.1 userspace 模式1.2 iptables 模式1.3 ipvs 模式 二、kube-proxy 启动参数基本参数目录挂盘kubeproxy配置项(ConfigMap)kube-proxy 启动参数 三、kube-proxy 常用命令四、宿主机上的iptables规则&…
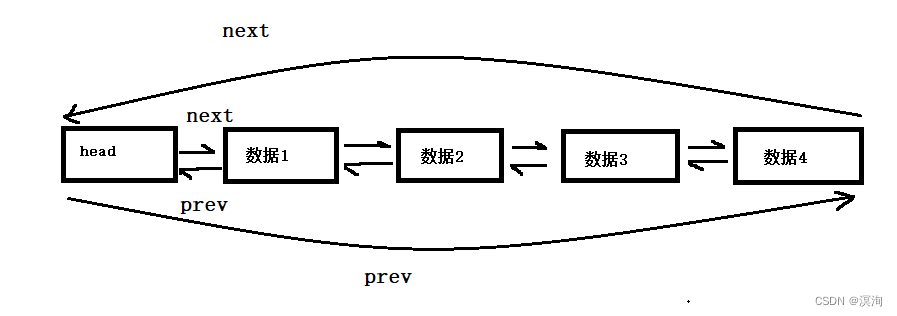
数据结构链表(C语言实现)
绪论 机遇对于有准备的头脑有特别的亲和力。本章将讲写到链表其中主要将写到单链表和带头双向循环链表的如何实现。 话不多说安全带系好,发车啦(建议电脑观看)。 附:红色,部分为重点部分;蓝颜色为需要记忆的…
【微服务】一文了解Nginx网关搭建教程
一文了解Nginx网关搭建教程 Nginx网关搭建nginx配置Nginx网关搭建
那么什么是Nginx呢?
nginx是一个高性能HTTP服务器,反向代理服务器,邮件代理服务器,TCP/UDP反向代理服务器。
单个系统主要用于处理客户端请求,一个系统处理客户端的请求量是有限的,当客户端的并发量超…
CROSSROADS: 1实战演练
文章目录 CROSSROADS: 1实战演练一、前期准备1、相关信息 二、信息收集1、端口扫描2、访问网站3、dirsearch扫描目录4、查看隐写5、枚举用户6、暴力破解7、访问共享文件夹8、查看第一个flag9、写入shell并连接 二、后渗透1、查看权限和SUID文件2、运行程序3、切换root3、查看第…
2019 - 2023,再见了我的大学四年
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,也会涉及到服务端(Node.js 等) 📃个人状态: 2023届本科毕业生,已拿多个前端 offer&#x…