目录
3.3 数字编码
3.3.1 原码、反码和补码
3.3.2 浮点数编码
3.3 数字编码
Tip
在本书中,标题带有 * 符号的是选读章节。如果你时间有限或感到理解困难,可以先跳过,等学完必读章节后再单独攻克。
3.3.1 原码、反码和补码
在上一节的表格中我们发现,所有整数类型能够表示的负数都比正数多一个,例如 byte 的取值范围是 [−128,127] 。这个现象比较反直觉,它的内在原因涉及原码、反码、补码的相关知识。
首先需要指出,数字是以“补码”的形式存储在计算机中的。在分析这样做的原因之前,首先给出三者的定义。
- 原码:我们将数字的二进制表示的最高位视为符号位,其中 0 表示正数,1 表示负数,其余位表示数字的值。
- 反码:正数的反码与其原码相同,负数的反码是对其原码除符号位外的所有位取反。
- 补码:正数的补码与其原码相同,负数的补码是在其反码的基础上加 1 。
图 3-4 展示了原码、反码和补码之间的转换方法。
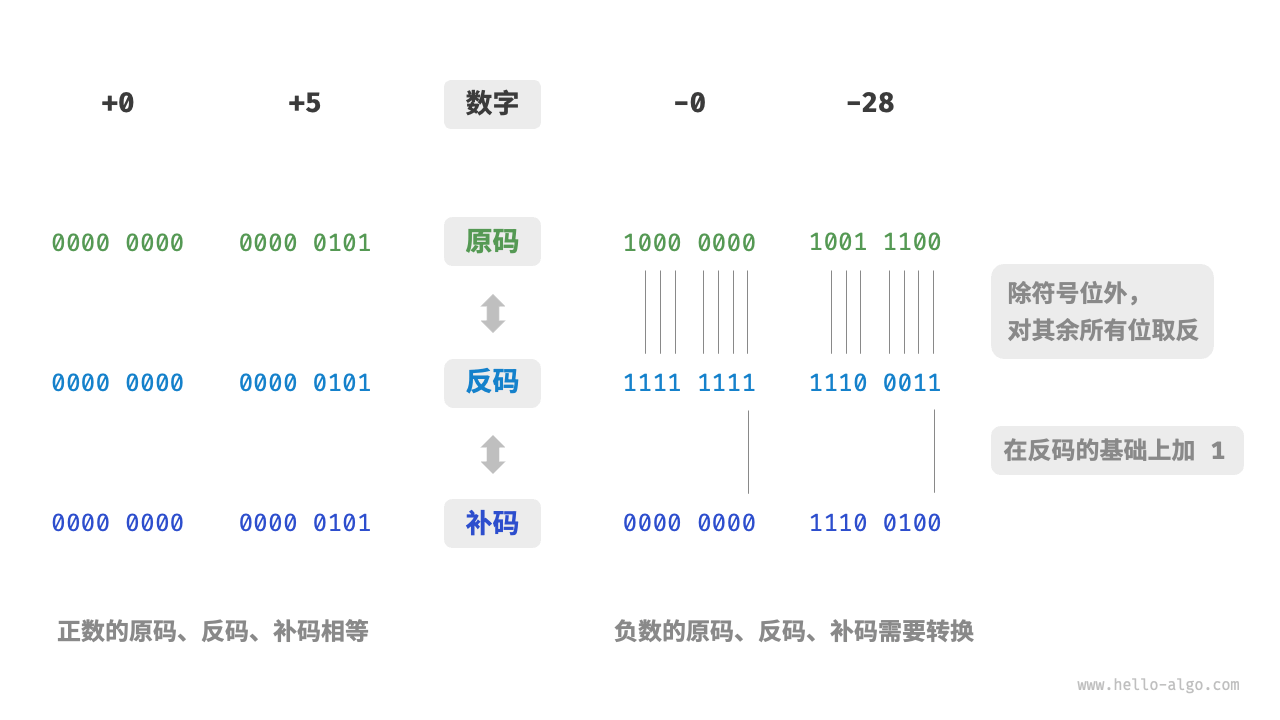
图 3-4 原码、反码与补码之间的相互转换
原码(sign-magnitude)虽然最直观,但存在一些局限性。一方面,负数的原码不能直接用于运算。例如在原码下计算 1+(−2) ,得到的结果是 −3 ,这显然是不对的。
1+(−2)→00000001+10000010=10000011→−3
为了解决此问题,计算机引入了反码(1's complement)。如果我们先将原码转换为反码,并在反码下计算 1+(−2) ,最后将结果从反码转换回原码,则可得到正确结果 −1 。
原码原码反码反码反码原码原码原码反码反码反码原码1+(−2)→00000001(原码)+10000010(原码)=00000001(反码)+11111101(反码)=11111110(反码)=10000001(原码)→−1
另一方面,数字零的原码有 +0 和 −0 两种表示方式。这意味着数字零对应两个不同的二进制编码,这可能会带来歧义。比如在条件判断中,如果没有区分正零和负零,则可能会导致判断结果出错。而如果我们想处理正零和负零歧义,则需要引入额外的判断操作,这可能会降低计算机的运算效率。
+0→00000000−0→10000000
与原码一样,反码也存在正负零歧义问题,因此计算机进一步引入了补码(2's complement)。我们先来观察一下负零的原码、反码、补码的转换过程:
原码反码补码原码反码补码−0→10000000(原码)=11111111(反码)=100000000(补码)
在负零的反码基础上加 1 会产生进位,但 byte 类型的长度只有 8 位,因此溢出到第 9 位的 1 会被舍弃。也就是说,负零的补码为 00000000 ,与正零的补码相同。这意味着在补码表示中只存在一个零,正负零歧义从而得到解决。
还剩最后一个疑惑:byte 类型的取值范围是 [−128,127] ,多出来的一个负数 −128 是如何得到的呢?我们注意到,区间 [−127,+127] 内的所有整数都有对应的原码、反码和补码,并且原码和补码之间可以互相转换。
然而,补码 10000000 是一个例外,它并没有对应的原码。根据转换方法,我们得到该补码的原码为 00000000 。这显然是矛盾的,因为该原码表示数字 0 ,它的补码应该是自身。计算机规定这个特殊的补码 10000000 代表 −128 。实际上,(−1)+(−127) 在补码下的计算结果就是 −128 。
原码原码反码反码补码补码补码原码原码反码反码补码补码补码(−127)+(−1)→11111111(原码)+10000001(原码)=10000000(反码)+11111110(反码)=10000001(补码)+11111111(补码)=10000000(补码)→−128
你可能已经发现了,上述所有计算都是加法运算。这暗示着一个重要事实:计算机内部的硬件电路主要是基于加法运算设计的。这是因为加法运算相对于其他运算(比如乘法、除法和减法)来说,硬件实现起来更简单,更容易进行并行化处理,运算速度更快。
请注意,这并不意味着计算机只能做加法。通过将加法与一些基本逻辑运算结合,计算机能够实现各种其他的数学运算。例如,计算减法 𝑎−𝑏 可以转换为计算加法 𝑎+(−𝑏) ;计算乘法和除法可以转换为计算多次加法或减法。
现在我们可以总结出计算机使用补码的原因:基于补码表示,计算机可以用同样的电路和操作来处理正数和负数的加法,不需要设计特殊的硬件电路来处理减法,并且无须特别处理正负零的歧义问题。这大大简化了硬件设计,提高了运算效率。
补码的设计非常精妙,因篇幅关系我们就先介绍到这里,建议有兴趣的读者进一步深入了解。
3.3.2 浮点数编码
细心的你可能会发现:int 和 float 长度相同,都是 4 字节 ,但为什么 float 的取值范围远大于 int ?这非常反直觉,因为按理说 float 需要表示小数,取值范围应该变小才对。
实际上,这是因为浮点数 float 采用了不同的表示方式。记一个 32 比特长度的二进制数为:
𝑏31𝑏30𝑏29…𝑏2𝑏1𝑏0
根据 IEEE 754 标准,32-bit 长度的 float 由以下三个部分构成。
- 符号位 S :占 1 位 ,对应 𝑏31 。
- 指数位 E :占 8 位 ,对应 𝑏30𝑏29…𝑏23 。
- 分数位 N :占 23 位 ,对应 𝑏22𝑏21…𝑏0 。
二进制数 float 对应值的计算方法为:
val=(−1)𝑏31×2(𝑏30𝑏29…𝑏23)2−127×(1.𝑏22𝑏21…𝑏0)2
转化到十进制下的计算公式为:
val=(−1)S×2E−127×(1+N)
其中各项的取值范围为:
S∈{0,1},E∈{1,2,…,254}(1+N)=(1+∑𝑖=123𝑏23−𝑖2−𝑖)⊂[1,2−2−23]
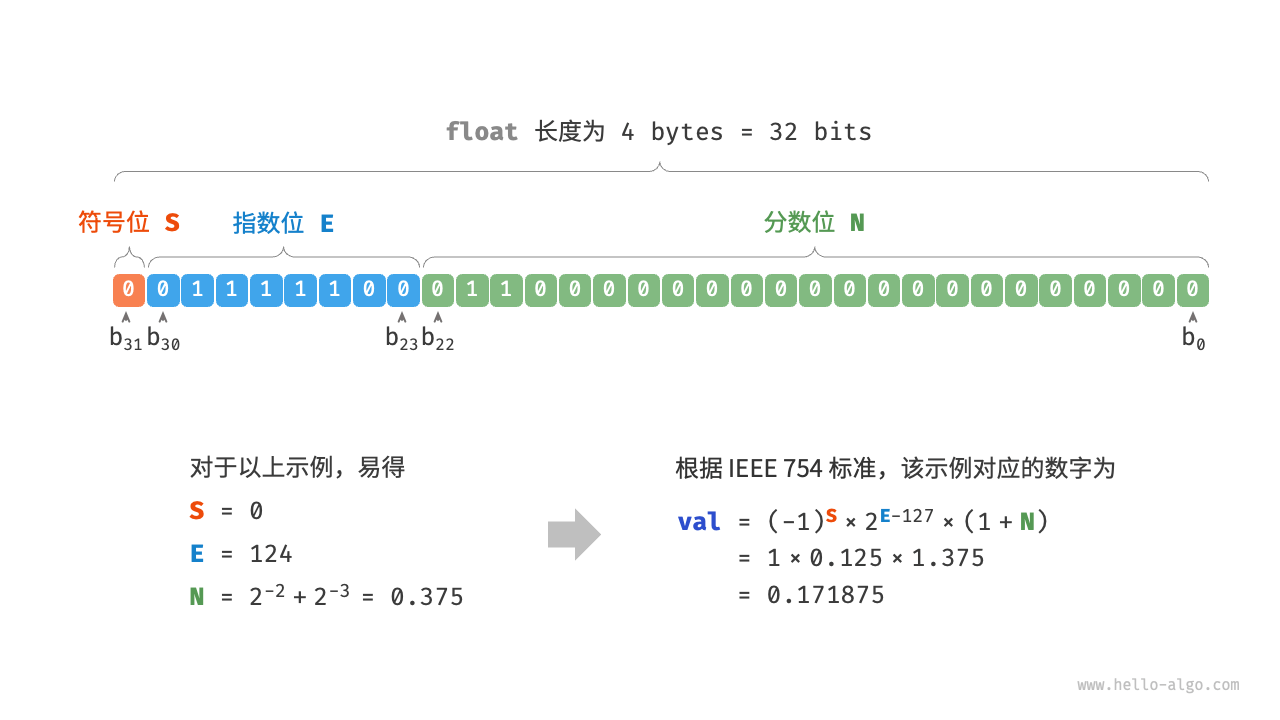
图 3-5 IEEE 754 标准下的 float 的计算示例
观察图 3-5 ,给定一个示例数据 S=0 , E=124 ,N=2−2+2−3=0.375 ,则有:
val =(−1)0×2124−127×(1+0.375)=0.171875
现在我们可以回答最初的问题:float 的表示方式包含指数位,导致其取值范围远大于 int 。根据以上计算,float 可表示的最大正数为 2254−127×(2−2−23)≈3.4×1038 ,切换符号位便可得到最小负数。
尽管浮点数 float 扩展了取值范围,但其副作用是牺牲了精度。整数类型 int 将全部 32 比特用于表示数字,数字是均匀分布的;而由于指数位的存在,浮点数 float 的数值越大,相邻两个数字之间的差值就会趋向越大。
如表 3-2 所示,指数位 E=0 和 E=255 具有特殊含义,用于表示零、无穷大、NaN 等。
表 3-2 指数位含义
| 指数位 E | 分数位 N=0 | 分数位 N≠0 | 计算公式 |
|---|---|---|---|
| 0 | ±0 | 次正规数 | (−1)S×2−126×(0.N) |
| 1,2,…,254 | 正规数 | 正规数 | (−1)S×2(E−127)×(1.N) |
| 255 | ±∞ | NaN |
值得说明的是,次正规数显著提升了浮点数的精度。最小正正规数为 2−126 ,最小正次正规数为 2−126×2−23 。
双精度 double 也采用类似于 float 的表示方法,在此不做赘述。