注：要视频学习可以去B站搜索“DR_CAN”讲解的卡尔曼滤波器，深有体会！

一、为啥需要卡尔曼滤波器

 

卡尔曼滤波器在生活中应用广泛，因为在我们生活中存在着不确定性，当我去描述一个系统，这个不确定性就包涵一下三点：

 所以要解决正样的问题，卡尔曼就诞生了。

1、下面我们进入公式推导，我们测量一个物品时，会存在测量读取误差以及测量工具误差，这时候我们正常采用多次测量取平均值来得出最终结果，那么下面我们就进行公式表达

 经过上述公式转换推导，是不是就出来了一个我们卡尔曼滤波器结果公式，其表达意思如下：

（1）既当前最优结果 = 上一次最优结果 + 卡尔曼增益*（此次测量值 - 上一次最优结果）

（2）随着测量次数的增加，当前次的测量结果就不那么重要了，反之测量次数比较少，那么当前次的结果作用就比较大。

（3）从公式也可以看出来，新的这一次X^k与上一次的估计值X^k-1有关，然后上一次的估计值X^k-1与上上次的有关，这就是一种递归思想。

（4）这也就是卡尔曼滤波器的优势，它不需要追溯很久以前的数据，只需要上一次的即可。

2、卡尔曼增益k

k在这里先做简单的解释，首先引入两个参数:

估计误差与测量误差，就是它们两个与真实值得差值

那么Kk的表达式：这里不做推导，这个公式是卡尔曼滤波器的核心公式

 

那么到这里，增益已经知道，我们把第一步的公式拿下来，合并起来

 是不是就可以转换成如下：

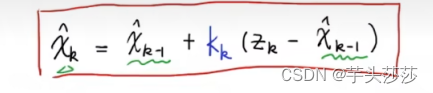
 3、估计误差与测量误差怎么确定参数？

估计上一次的误差同时初始化是为  kfp.Last_P = 1;切记不可为0

测量误差：这个取决于传感器的精度，如果你的传感很贵精度很厉害那这个测量误差你可以取0.1等，可以实际调试看看最终结果。

4、根据上面理解与公式，我们来做一维的滤波处理

eg:

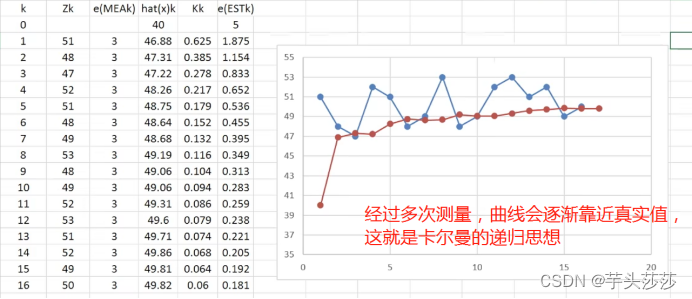 如果用程序表达

typedef struct

{

    float Last_P;//上次估算协方差 不可以为0 ! ! ! ! !

    float estout ;//卡尔曼滤波器输出

    float Kg;//卡尔曼增益

    float R;//(测量)观测噪声协方差

}Kalman;

Kalman kfp;

void Kalman_Init(void)

{

kfp.Last_P = 5;

kfp.estout = 40;

kfp.Kg = 0;

kfp.R = 3;//这个取决于传感器的精度

}

Void KalmanPro(float kfpMeak)

{

kfp.Kg = kfp.Last_P / (kfp.Last_P + kfp.R );

kfp.estout = kfp.estout + kfp.Kg(kfpMeak - kfp.estout);

kfp.Last_P = (1- kfp.Kg)*kfp.Last_P;

}