概述

最近研究超平面排列(Hyperplane Arrangement)问题的时候，发现ReLU有其缺陷，即举例来说，ReLU 无法使用单一的超平面将分离的所有数据，完整的输出，即只会输出半个空间映射的数据，而另一半空间的数据被置为0; ReLU 要完整的映射输入空间的所有数据需要至少3个节点才能办到，比如在2维的输入空间上，当只有2个节点时构成的超平面排列将输入空间划分4个区域，其中其中一定有一个区域全部输出为[0,0]即所谓的死区(Dead Region)，死区在ReLU的网络中是普遍问题。

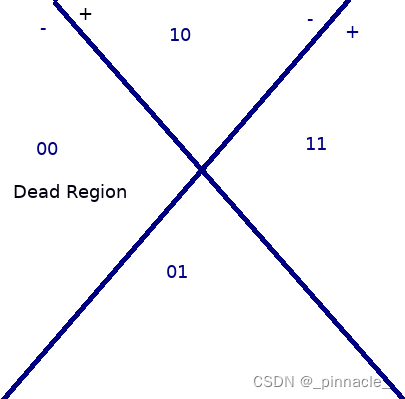
所以想用ReLU的网络构造基于二叉树结构的网络是不行的。而二叉树有非常好的性质，在分类问题上表现为无限层的二叉空间划分一定可以将输入空间中任意一点分类为所属类别，即无限逼近能力，这是一个非常强大的性质。而基于softmax的激活函数却能构造出这样的性质，而且该激活函数是构成self-attention的重要组成，后文会详细介绍。

Softmax函数

softmax函数在深度学习中被广泛使用，其公式也比较简单：
$$softmax(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}$$其中 i ∈ { 1 , 2 , . . , n } i \in \{1,2,..,n\} i∈{1,2,..,n} ，$n$为大于1的自然数，且$softmax(z_i)$的值域为$[0,1]$。softmax函数的作用即是求任意的节点值的指数与所有节点值的指数和的比值。

softmax函数也可以写为向量形式
$$softmax(z)=\frac{e^z}{{\sum }_{j=1}^n{e}^{z_j}}$$其中$z\in R^n$，即$z$为$n$维实向量，这里$z_j$表示$z$的第$j$维数据。

基于Softmax的激活函数

我们知道softmax本身也是激活函数，但是一般只在分类层使用，方便训练时反向传播或测试时获得近似的概率值，而很少被用于隐藏层中。但是self-attention与transformer的流行，使得softmax在隐藏层中被大量使用也产生了很好的效果，本节将解析一种基于softmax的激活函数，并研究其性质，最后解释这种激活函数与Seft-Attention的关系。

在讲解基于Softmax的激活函数之前先定义softmax的hard形式，方便解释其运行原理
$$hardmax(z_i)=\{\begin{array}{cc}0& z_i\ne \max (z_1,...,z_n)\\ 1& z_i=\max (z_1,...,z_n)\end{array}$$ 即对于所有的输入，该输入如果不是最大值则为0，如果为最大值则为1。为了方便我们也将其写为向量形式（这个其实就是one-hot形式的表示）。
$$hardmax(z)=hardmax([z_1,..,z_n])=\begin{array}{c}[hardmax(z_1),...,hardmax(z_n)]\end{array}$$ 对于有2个输出节点的神经网络而言，其结构如图：

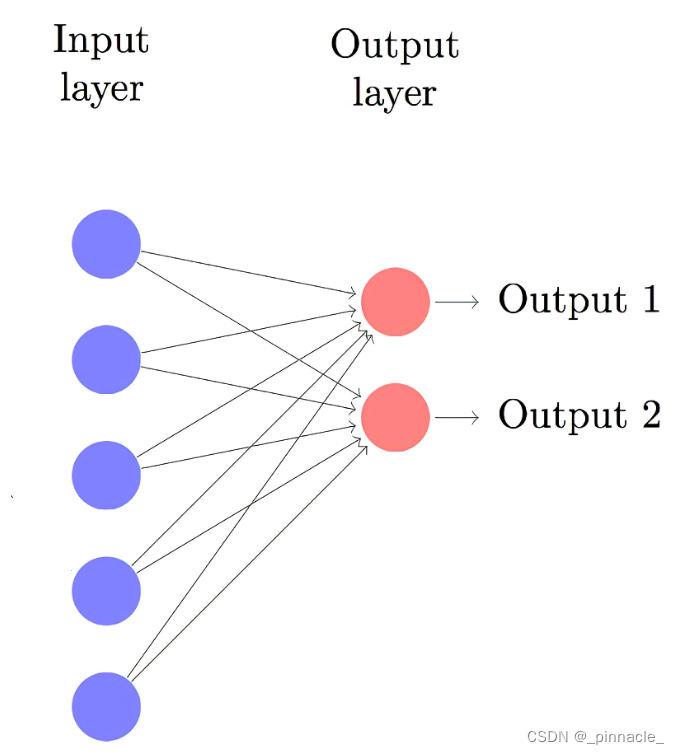
各节点的公式可以表示为：
$$y_1=w_1^{\mathsf{T}}x+b_1$$ $$y_2=w_2^{\mathsf{T}}x+b_2$$ 将输出表示为向量形式$V=[y_1,y_2{]}^{\mathsf{T}}$，我们构造以下函数（这个函数其实就是maxout激活函数的等价形式）：
$$maxout(x)=hardmax(V^{\mathsf{T}})V$$显然，$hardmax(V^{\mathsf{T}})$只可能为$[0,1]$或$[1,0]$，那么可以得到
$$maxout(x)=\{\begin{array}{cc}{y}_1& y_1\ge y_2\\ y_2& y_1<y_2\end{array}$$可以推出
$$maxout(x)=\{\begin{array}{cc}{y}_1& w_1^{\mathsf{T}}x+b_1\ge w_2^{\mathsf{T}}x+b_2\\ y_2& w_1^{\mathsf{T}}x+b_1<w_2^{\mathsf{T}}x+b_2\end{array}$$做一次代数替换，令$w^{\mathsf{T}}=(w_1-w_2{)}^{\mathsf{T}}$，$b=b_1-b_2$，那么可得
$$maxout(x)=\{\begin{array}{cc}{y}_1& w^{\mathsf{T}}x+b\ge 0\\ y_2& w^{\mathsf{T}}x+b<0\end{array}$$我们发现与ReLU是比较相似的
$$ReLU(x)=\{\begin{array}{cc}{w}^{\mathsf{T}}x+b& w^{\mathsf{T}}x+b\ge 0\\ 0& w^{\mathsf{T}}x+b<0\end{array}$$ 我们知道ReLU构造的超平面为 H = { x ∣ w T x + b = 0 } H=\{ x|w^\mathsf{T}x +b = 0 \} H={x∣wTx+b=0}，同理$maxout(x)$也是一样的，与ReLU不同的是，ReLU只输出超平面一侧的数据，而丢弃了另一侧的数据；而$maxout(x)$可以输出两侧的数据，且只使用单个超平面就能实现，也就是说这个函数不存在所谓的死区问题，这是一个非常良好的性质。

以上描述了很多，其实是想引出maxout的soft形式，那么
$$maxou{t}_{soft}(x)=softmax(V^{\mathsf{T}})V$$对于2个节点，当$y_1=y_2$时，$softmax(y_1)=softmax(y_2)=0.5$，所以$softmax$的这种形式并不影响上述内容$hardmax$形式的超平面位置，也就不影响上面得到的结论，唯一的区别是softmax最后的输出是soft形式（各节点值加权平均）的$y$值，即
$$y=\sum _{i=1}^n{\alpha }_i\ast y_i$$其中 ${\sum }_{i=1}^n{\alpha }_i=1$，这里$n=2$，当任意${\alpha }_i=1$时，$maxou{t}_{soft}(x)$ 退化为 $maxout(x)$的形式。

当$n\ge 3$个节点时，也是同理，$softmax$也不影响超平面的位置，多个节点的网络会使用超平面排列（Hyperplane Arrangement）构造出类似下图的决策边界

对于$maxout(x)$当某个节点为最大值时，网络构造的分类区域中一个区域会被直接输出，如上图中3个节点的网络会有1个区域（完整包含1类模式，如蓝色区域）的数据输出，而$maxou{t}_{soft}(x)$则是根据$softmax$获取的权值，加权后输出。

以上就是 $softmax$ 的性质的描述，且构造了$$maxou{t}_{soft}(x)=softmax(V^{\mathsf{T}})V$$的激活函数，其实我们会发现这个形式和self-attention是非常相似的，那么这个激活函数是否就是self-attention的等价形式呢？这个是接下来要研究的问题。

Self-Attention原理初步

上文构造了类self-attention的激活函数，而self-attention的公式为：
$$Attention(Q,K,V)=softmax(\frac{1}{\sqrt{d_k}}Q{K}^{\mathsf{T}})V$$其中Q,K,V分别表示Query,Key,Value，且
$$Q=x{W}_q$$ $$K=x{W}_k$$ $$V=x{W}_v$$即Q,K,V都是 $x$ 经过线性变换后的数据，而$\frac{1}{\sqrt{d_k}}$只是避免矩阵乘值过大的超参数，本质上说self-attention的核心内容为：

$$Attention(x)=softmax(x{W}_q(x{W}_k{)}^{\mathsf{T}})V$$可以写为
$$Attention(x)=softmax(x(W_q{W}_k^{\mathsf{T}})x^{\mathsf{T}})V$$令$\tilde{W}=W_q{W}_k^{\mathsf{T}}$，其中$\tilde{W}$是一个方阵，可以得到
$$Attention(x)=softmax(x\tilde{W}{x}^{\mathsf{T}})V$$而不管$w^{\mathsf{T}}x+b$ 或者 $xW$本质都是一样的，即$x$的线性变换；我们可以令$W=w^{\mathsf{T}}$，将$b$写到$W$当中可以得到$Wx$，所以两者是形式等价的，$xW$的形式更方便程序计算。所以上节中的
$$maxou{t}_{soft}(x)=softmax(V^{\mathsf{T}})V$$与self-attention的不同之处是$x\tilde{W}{x}^{\mathsf{T}}$与$x{W}_v$的区别，权值不同很好理解，Attention使用了新的权值矩阵，且$\tilde{W}$是$n\times n$方阵，而$W_v$是$n\times m$的矩阵；另一个不同是$x{W}_v$只是$x$的一个简单线性变换，而$x\tilde{W}{x}^{\mathsf{T}}$则不是这样的。

为了论述方便，我们假设当$\tilde{W}$为对角矩阵时，如

$$diag([1,1,1])=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
$x\tilde{W}{x}^{\mathsf{T}}$退化为了$x{x}^{\mathsf{T}}$，而$x{x}^{\mathsf{T}}$一般用于协方差矩阵（Covariance Matrix）或相关矩阵（Correlation Matrix），而不管是协方差矩阵还是相关矩阵都可以用于描述矩阵各行，列向量之间的相关程度或相关关系，自协方差矩阵公式是这样的
$$Co{v}_{x,y}=E((x-\bar{x})(x-\bar{x}{)}^{\mathsf{T}})=\left[\begin{array}{ccc}{c}_{x_1,y_1}& \dots & c_{x_1,y_N}\\ \dots & \dots & \dots \\ c_{x_N,y_1}& \dots & c_{x_N,y_N}\end{array}\right]$$
其中$c_{x_n,x_n}$表示两元素的方差，其中 n ∈ { 1 , . . , N } n\in\{1,..,N\} n∈{1,..,N}，而自相关矩阵是这样的
$$R_{x,x}=E(x{x}^{\mathsf{T}})=\left[\begin{array}{ccc}{r}_{x_1,x_1}& \dots & r_{x_1,x_N}\\ \dots & \dots & \dots \\ r_{x_N,x_1}& \dots & r_{x_N,x_N}\end{array}\right]$$
其中$r_{x_n,x_n}$表示两元素相关系数。我们再把$\tilde{W}$设置为普通的方阵，那么$x\tilde{W}{x}^{\mathsf{T}}$则表示经过$\tilde{W}$线性映射的$x$与$x$自身的相关关系矩阵。

有了相关关系的矩阵，便可以通过softmax函数获取每个元素的权值，如在自然语言里，就是每个单词的权值，再乘$V$就是每个单词关于句子加权求和之后的表示，即所谓的Attention。

所以，$maxou{t}_{soft}(x)$ 与 self-attention还是不太相同的，而self-attention确实用到了$maxou{t}_{soft}(x)$的激活函数的性质。

总结

self-attention部分写的有点粗糙，大概解析了self-attention的部分逻辑，后面有新的内容再补充。

参考

1. Maxout networks
2. Attention Is All You Need
3. Understand Maxout Activation Function in Deep Learning
4. Correlation coefficients
5. Scan and Snap: Understanding Training Dynamics and Token Composition in 1-layer Transformer
6. Understanding the Covariance Matrix