形象图
里面的my_Kalman.ipynb 和ppt就是了,其他的是原始资料和 辅助函数
链接:https://pan.baidu.com/s/1J1nA–oqoj8OvgbrA3LfbQ?pwd=1264
提取码:1264
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# 定义卡尔曼滤波器类
class KalmanFilter:
def __init__(self, dt, sigma_a, sigma_z):
self.dt = dt # 时间步长
self.sigma_a = sigma_a # 过程噪声的标准差
self.sigma_z = sigma_z # 观测噪声的标准差
self.A = np.array([[1, 0, dt, 0],
[0, 1, 0, dt],
[0, 0, 1, 0],
[0, 0, 0, 1]]) # 状态转移矩阵
self.Q = np.array([[dt**4/4, 0, dt**3/2, 0],
[0, dt**4/4, 0, dt**3/2],
[dt**3/2, 0, dt**2, 0],
[0, dt**3/2, 0, dt**2]]) * sigma_a**2 # 过程噪声协方差矩阵
self.H = np.array([[1, 0, 0, 0],
[0, 1, 0, 0]]) # 观测矩阵
self.R = np.array([[sigma_z**2, 0],
[0, sigma_z**2]]) # 观测噪声协方差矩阵
self.mu = np.zeros((4, 1)) # 状态向量
self.sigma = np.eye(4) # 状态协方差矩阵
# 预测状态和协方差
def predict(self):
self.mu = self.A @ self.mu
self.sigma = self.A @ self.sigma @ self.A.T + self.Q
# 更新状态和协方差
def update(self, z):
K = self.sigma @ self.H.T @ np.linalg.inv(self.H @ self.sigma @ self.H.T + self.R)
self.mu = self.mu + K @ (z - self.H @ self.mu)
self.sigma = (np.eye(4) - K @ self.H) @ self.sigma
# 获取当前状态向量
def get_state(self):
return self.mu.flatten()[:2]
# 初始化参数
dt = 0.1 # 时间步长
sigma_a = 0.5 # 过程噪声的标准差
sigma_z = 1 # 观测噪声的标准差
u = np.array([1, 0.5, 0, 0]) # 物体的速度和加速度
x_real = np.array([0, 0]) # 物体的真实位置
kf = KalmanFilter(dt, sigma_a, sigma_z) # 初始化卡尔曼滤波器
# 绘制预测结果的动态可视化
fig, ax = plt.subplots()
xdata_real, ydata_real = [], []
xdata_pred, ydata_pred = [], []
line_real, = ax.plot([], [], 'o', color='blue')
line_pred, = ax.plot([], [], '-', color='red')
def init():
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
return line_real, line_pred
def update(frame):
global x_real, u, kf
# 更新物体的真实位置
x_real = x_real + u[:2] * dt
# 产生观测值
z = x_real + np.random.randn(2) * sigma_z
# 进行预测和更新
kf.predict()
kf.update(z)
# 绘制真实位置和预测位置
xdata_real.append(x_real[0])
ydata_real.append(x_real[1])
line_real.set_data(xdata_real, ydata_real)
x_pred, y_pred = kf.get_state()
xdata_pred.append(x_pred)
ydata_pred.append(y_pred)
line_pred.set_data(xdata_pred, ydata_pred)
return line_real, line_pred
ani = FuncAnimation(fig, update, frames=range(100), init_func=init, blit=True)
# 保存动态图为gif文件
ani.save('kalman_filter_prediction.gif', writer='pillow')
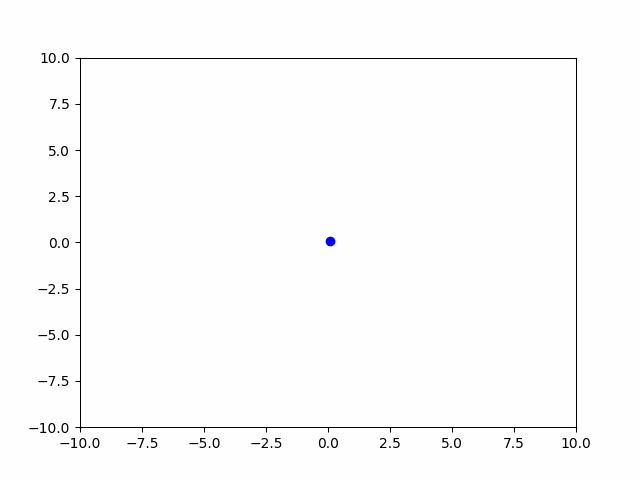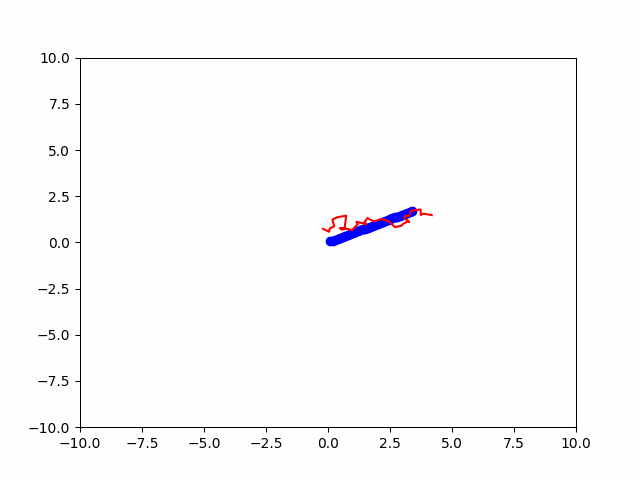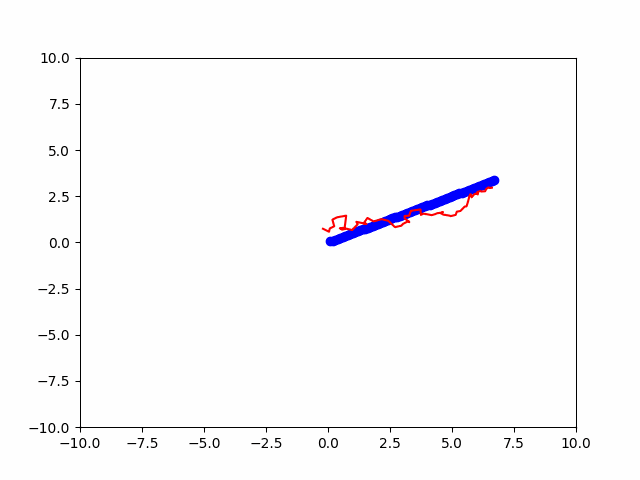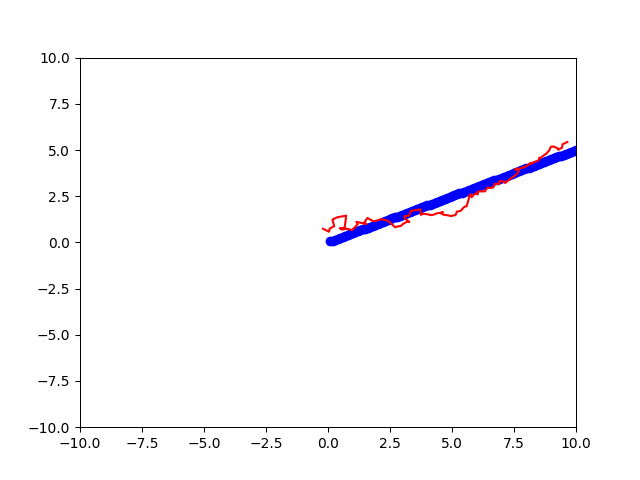
我们定义了一个KalmanFilter类来实现卡尔曼滤波器。在update函数中,我们首先更新物体的真实位置,然后生成观测值,接着使用卡尔曼滤波器进行预测和更新,并将真实位置和预测位置绘制在图像上。同时,我们使用FuncAnimation函数将预测结果进行动态可视化,并使用ani.save函数将动态图保存为gif文件。
执行代码后,会在当前工作目录下生成名为kalman_filter_prediction.gif的文件,其中包含了绘制的动态图。您可以使用任何支持gif格式的图像查看器打开它。
卡尔曼滤波器是一种算法,它利用随时间观测到的一系列测量来估计系统的状态。它被广泛应用于许多不同的工程和科学领域,包括控制系统、信号处理和机器人学。
在高层次上,卡尔曼滤波器通过组合两个信息流来工作:关于系统当前状态的预测和系统实际状态的测量。滤波器使用这两个信息流来迭代更新其对系统状态的估计,并计算该估计的不确定性(或协方差)。
更具体地说,卡尔曼滤波器遵循一个递归过程,其中包括以下步骤:
-
预测:滤波器根据先前对状态的估计和系统的动态(即状态随时间的演变)预测系统的当前状态。这个预测是基于一个状态转移模型,描述了状态随时间的演变,以及一个过程噪声模型,考虑了任何预测中的不确定性或误差。
-
更新:滤波器将系统的新测量(即观测值)纳入其中,并根据预测状态与观测状态之间的差异更新其对状态的估计。这个更新是基于一个测量模型,描述了测量与系统状态的关系,以及一个测量噪声模型,考虑了测量中的任何不确定性或误差。
-
重复:滤波器重复执行这些步骤,使用更新后的状态估计作为下一个时间步的预测,并纳入新的测量来改进其估计。
卡尔曼滤波器旨在最小化估计状态和系统真实状态之间的均方误差。它通过使用一组数学方程最小化估计状态和真实状态之间的期望平方误差,给定可用的测量和预测来实现这一点。
总体而言,卡尔曼滤波器是一种在存在不确定性和噪声的情况下估计系统状态的强大工具。它被广泛应用于许多不同的领域,并已被证明在广泛的应用中是有效的。
 https://www.bilibili.com/video/BV1GB4y1D7P1/?spm_id_from=333.788&vd_source=569ef4f891360f2119ace98abae09f3f
https://www.bilibili.com/video/BV1GB4y1D7P1/?spm_id_from=333.788&vd_source=569ef4f891360f2119ace98abae09f3f
什么是卡尔曼滤波
卡尔曼滤波(Kalman Filter)是一种用于估计状态空间模型中状态变量的算法,它可以通过系统的动态方程和观测方程,递归地计算和更新状态的估计值和误差协方差矩阵。卡尔曼滤波算法最初是由R.E. Kalman在1960年提出来的,后来被广泛应用于控制、信号处理、航空航天、无线通信、机器人等领域。
卡尔曼滤波的基本思想是:通过对系统状态及其误差的估计,结合观测数据对系统状态进行更新,从而提高对系统状态的估计精度。具体来说,卡尔曼滤波算法包含以下几个步骤:
-
预测:根据系统的动态方程,利用前一时刻的状态估计值和误差协方差矩阵,预测当前时刻的状态估计值和误差协方差矩阵。
-
更新:根据观测方程,利用当前时刻的观测数据和预测的状态估计值,计算当前时刻的状态估计值和误差协方差矩阵。
-
递归:重复进行预测和更新,逐步逼近真实的系统状态。
卡尔曼滤波算法的优点是可以对系统状态进行实时估计,同时考虑了系统的动态特性和观测噪声。它可以在噪声较大、观测数据存在缺失等情况下,仍然能够对系统状态进行较为准确的估计。缺点是需要对系统的动态方程和观测方程进行建模,对模型的准确性和参数的选择有一定要求。




 如果火箭被遮挡住了怎么办?
如果火箭被遮挡住了怎么办?
跟踪运动,也称为运动跟踪,是指在视频或图像序列中自动或半自动地跟踪目标的位置和运动。跟踪运动可以用于许多应用程序,如视频监控、自动驾驶、机器人导航、运动分析等。
跟踪运动的目标通常是一个或多个运动中的物体,如人、车、球等。跟踪运动的过程通常涉及以下步骤:
-
目标检测:在视频或图像序列中检测出目标物体的位置和大小。
-
特征提取:提取目标物体的特征,如颜色、纹理、形状等。
-
相似度度量:计算目标物体在相邻帧中的相似度,以确定目标的运动方向和速度。
-
目标跟踪:根据目标物体在前几帧中的位置和运动信息,估计目标在当前帧中的位置和运动信息。
跟踪运动是一项复杂的任务,需要应用计算机视觉和机器学习等技术来实现。常用的跟踪算法包括Kalman滤波器、粒子滤波器、相关滤波器、光流法等。
什么叫跟踪运动?
观测
预测
观测

运动建模
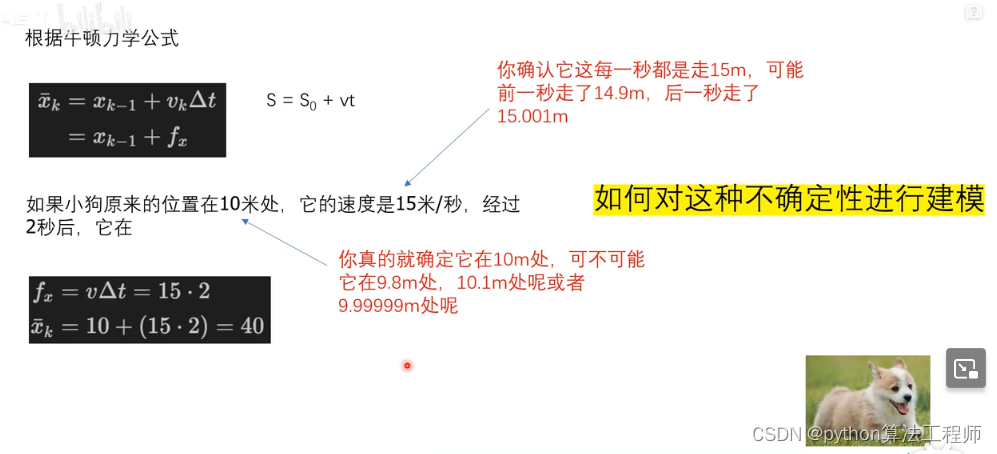

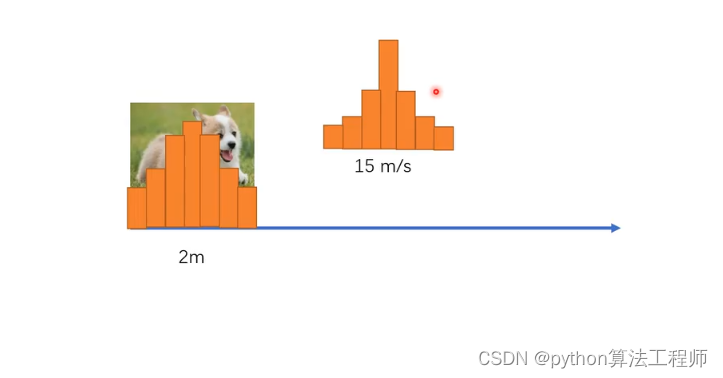 高斯分布
高斯分布
由于狗狗运动的不确定性所以对狗狗进行建模,使用高斯分布进行建模
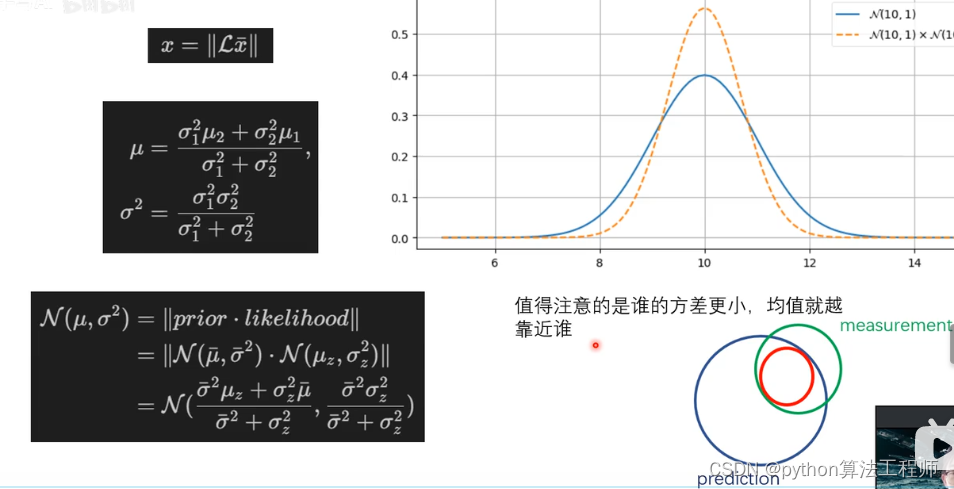
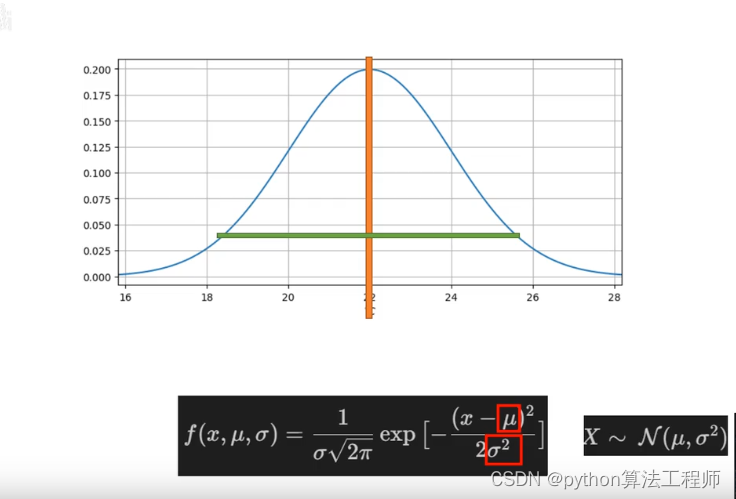 高斯分布仅仅用两个变量进行描述,均值和方差
高斯分布仅仅用两个变量进行描述,均值和方差
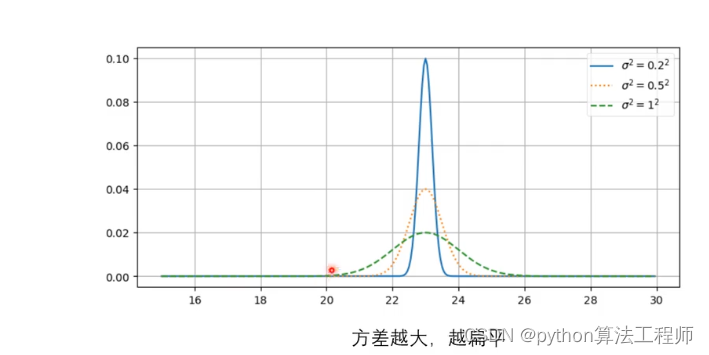

高斯分布进行相加和相乘之后依然是高斯分布的
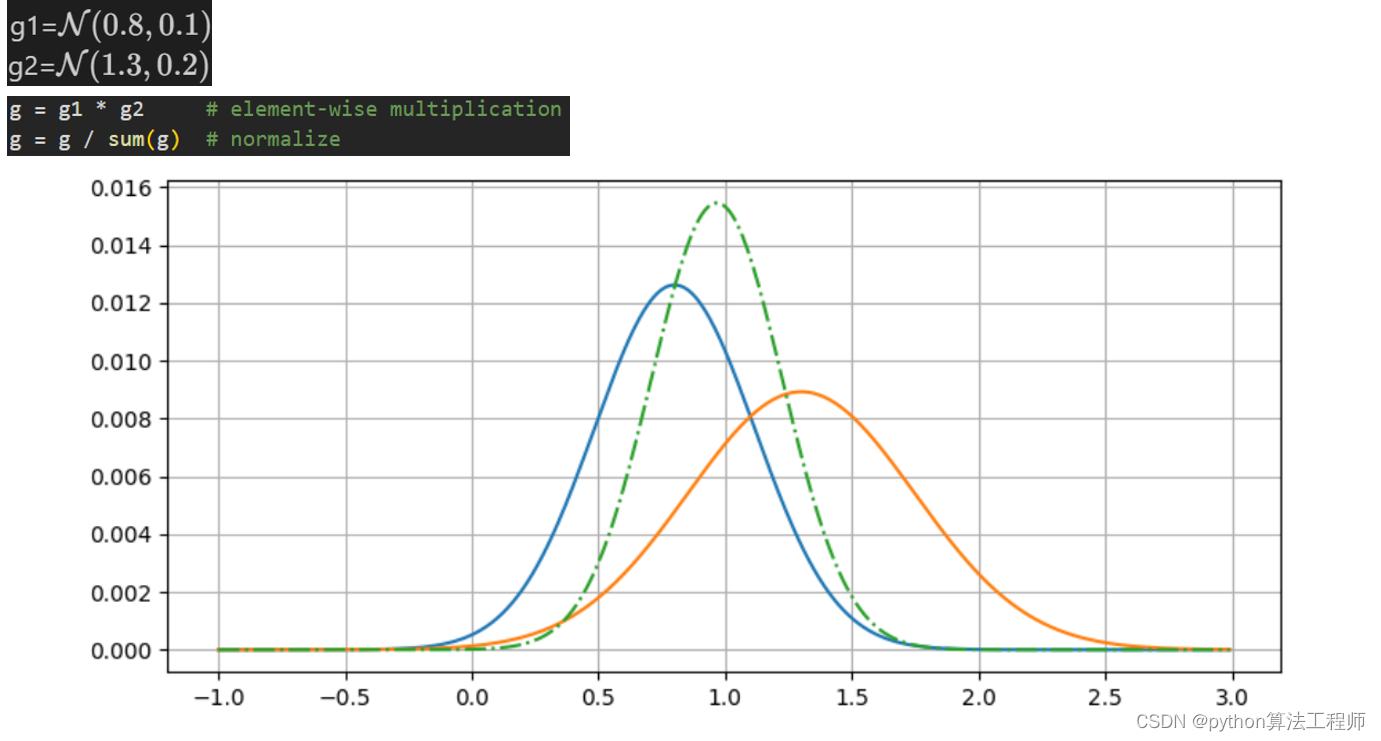
绿色虚线是由蓝色和黄色相加生成的
新的高斯分布均值在原来两个均值之间
方差变小,变得更加高瘦
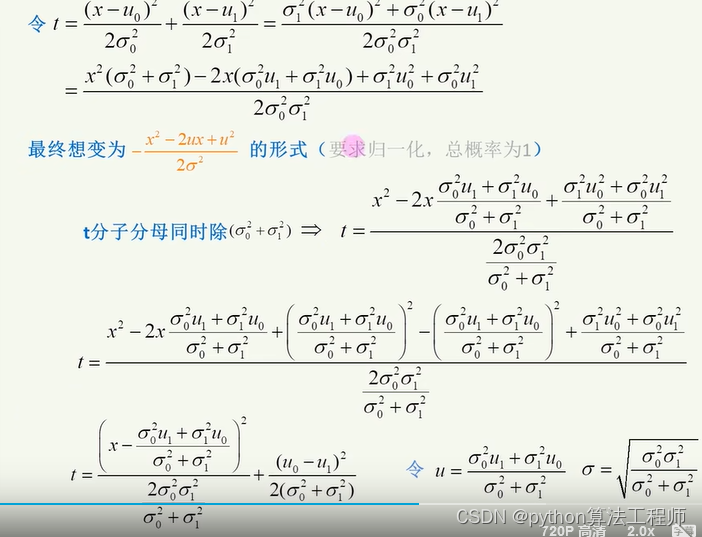
高斯分布下的运动预测
基于原始的数据所建立的一个模型
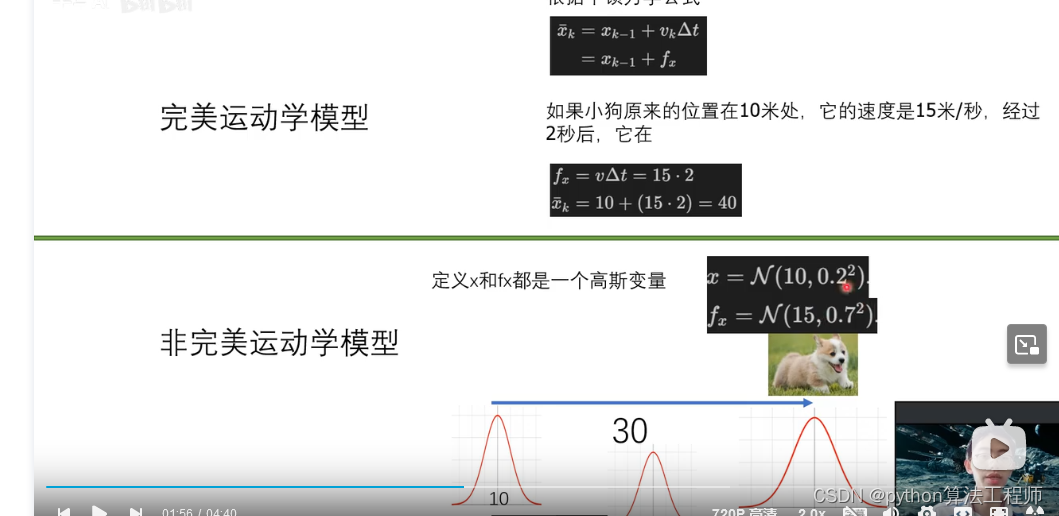 非完美的运动学模型的方差会更大一下,因为他的不确定性更大
非完美的运动学模型的方差会更大一下,因为他的不确定性更大
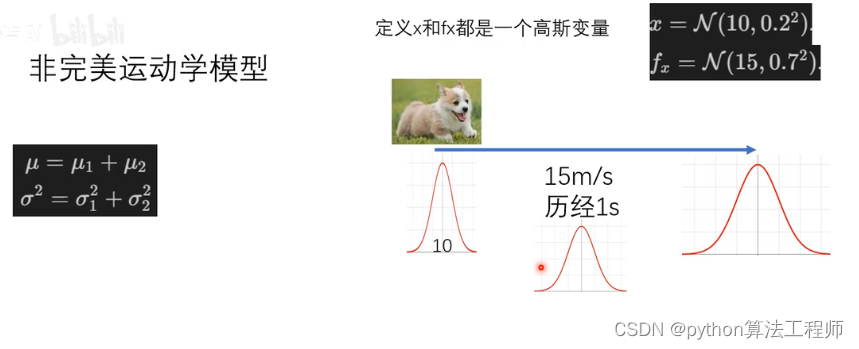


 用观测矫正误差
用观测矫正误差
优化算法:使用优化算法,如扩展卡尔曼滤波器(EKF)、无迹卡尔曼滤波器(UKF)等,对机器人或车辆的位置和运动进行优化。这些算法可以通过对测量结果和模型进行联合估计,减少误差累积,并提高位置和运动的准确性。
卡尔曼滤波(Kalman Filter)是一种用于估计系统状态的算法,可以用于矫正机器人或车辆等移动系统中的位置和运动误差。卡尔曼滤波的基本原理是通过对系统状态的预测和测量结果的融合,估计系统的真实状态,并降低其估计误差。
以下是使用卡尔曼滤波矫正位置和运动误差的一般步骤:
-
确定状态变量:确定系统的状态变量,例如机器人或车辆的位置、速度、加速度等。
-
建立状态转移模型:建立状态转移模型,描述系统状态在时间上的变化。例如,可以使用运动学模型描述机器人或车辆的运动行为。
-
建立观测模型:建立观测模型,描述系统状态和测量结果之间的关系。例如,可以使用传感器测量机器人或车辆的位置和运动,建立观测模型。
-
初始化:初始化系统状态和卡尔曼滤波器的状态。通常,将系统状态设置为初始位置和速度,并将卡尔曼滤波器的状态设置为初始状态。
-
预测:使用状态转移模型,预测系统的状态和协方差矩阵。预测的状态和协方差矩阵将作为下一步的输入。
-
测量更新:使用观测模型和测量结果,对系统状态和协方差矩阵进行更新。根据卡尔曼滤波的原理,测量结果将用于校正预测的状态和协方差矩阵。
-
循环迭代:重复执行步骤5和6,直到达到预设条件或满足精度要求。
通过这些步骤,可以使用卡尔曼滤波矫正移动系统中的位置和运动误差,并提高其位置和运动的准确性。需要注意,卡尔曼滤波的效果受到状态转移模型和观测模型的准确性和精度的影响,因此需要根据具体情况进行调整和优化。
手写高斯分布的运动预测代码
#namedtuple
#先写一个高斯类
#导入命名元组
from collections import namedtuple
#gaussian表示一个高斯分布mean表示均值,var表示方差
gaussian = namedtuple("Gaussian",["mean","var"])
#打印出属性
gaussian.__repr__ = lambda s:f"N(mean={s[0]:.3f},var ={s[1]:.3f})"
g1 = gaussian(3.4,10.1)
g2 = gaussian(mean = 4.5, var = 0.2**2)
print(g1)
print(g2)
g1.mean,g2.var
N(mean=3.400,var =10.100)
N(mean=4.500,var =0.040)

#高斯相加
def predict(pos,movement):
#均值相加,方差相加
return gaussian(pos.mean+movement.mean,pos.var+movement.var)
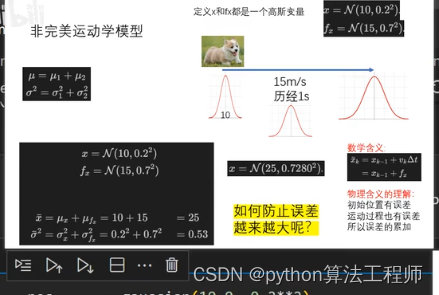
高斯分布下的预测

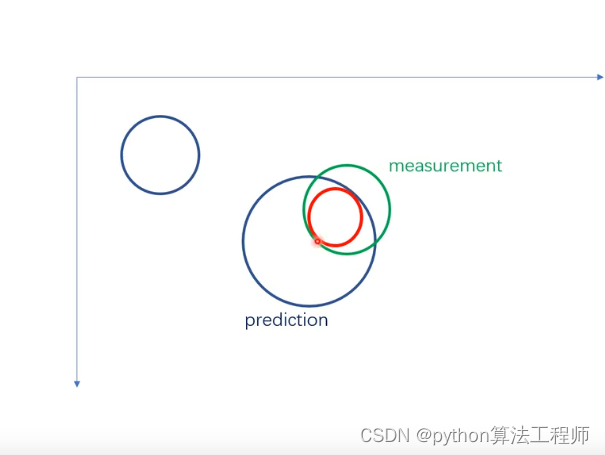 取两个高斯的交集
取两个高斯的交集

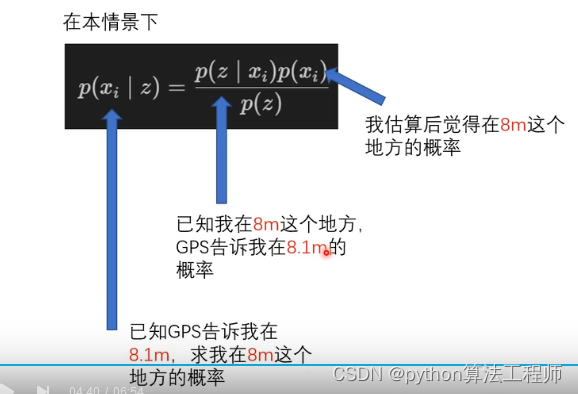
代码演示
#高斯相乘的函数
def gaussian_multiply(g1,g2):
mean = (g1.var*g2.mean+g2.var*g1.mean)/(g1.var+g2.mean)
variance = (g1.var*g2.var)/(g1.var+g2.var)
return gaussian(mean,variance)
#更新
def update(likelihood,prior)
posterior = gaussian_multiply(likelihood,prior)
return posterior
predicted_pos = gaussian(10.0,0.2**2)
measured_pos = gaussian(11.0,0.1**2)
estimated_pos = update(predicted_pos,measured_pos)
print(measured_pos)
print(predicted_pos)
print(estimated_pos)
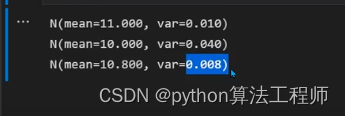 当我们将观测结果和预测结果结合起来,我们会发现方差变小了
当我们将观测结果和预测结果结合起来,我们会发现方差变小了
将多个数据源进行加权平均之后,会更加确定
你的第一个卡尔曼滤波器


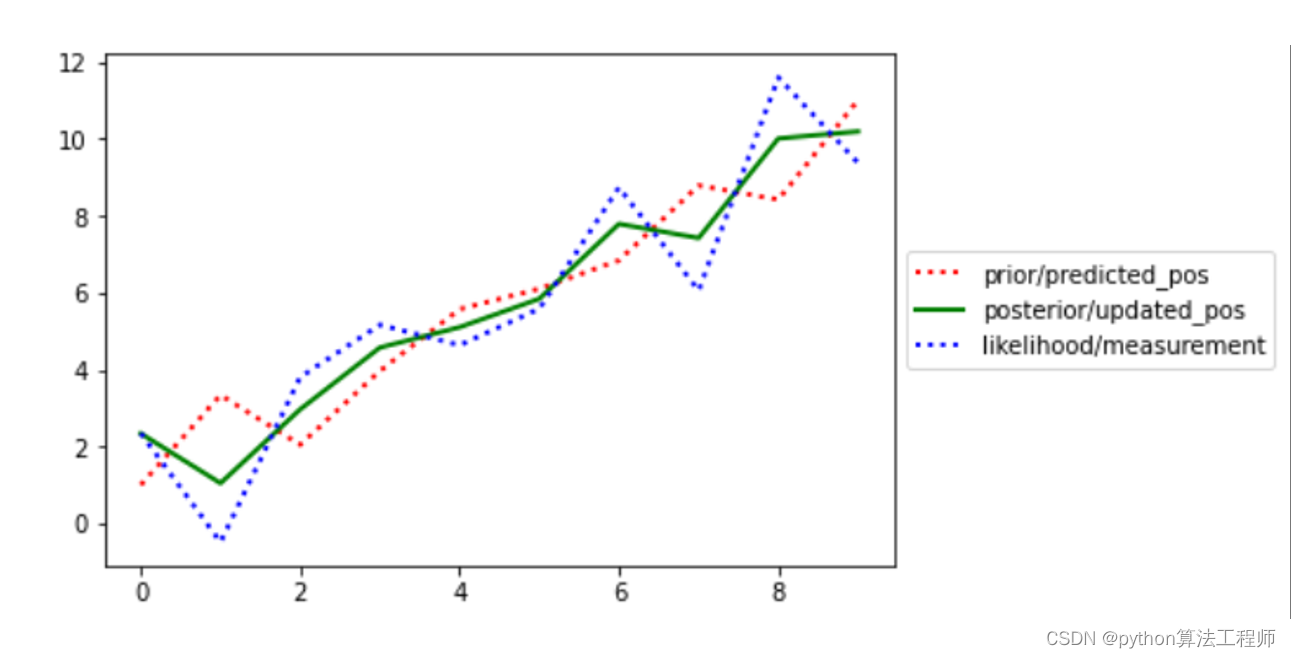 蓝色和红色都是数据源
蓝色和红色都是数据源
绿色是过滤掉噪声之后的
import numpy as np
from numpy.random import randn
from math import sqrt
import matplotlib.pyplot as plt
def print_result(predict,update,z,epoch):
#predicted_pos,updated_posclear,measured_pos
predict_template = '{:3.0f} {:7.3f} {:8.3f}'
update_template = '\t{:.3f}\t{:7.3f}{:7.3f}'
print(predict_template.format(epoch,predict[0],predict[1],end='\t'))
print(update_templatre.format(z,update[0],update[1]))
def plot_result(epochs,prior_list,x_list,z_list):
epoch_list = np.arrange(epochs)
plt.plot(epoch_list,prior_list,linestyle = ':',color = 'r',label = "prior/predicted_pos",lw=2)
plt.plot(epoch_list,z_list,linestyle = ":",color = 'b',label = "posterior/updated_pos",lw =2)
plt.plot(epoch_list,z_list,linestyle=":",color = 'b',label = "likelihood.measurement",lw = 2)
plt.legent(loc = "center left",bbox_to_anchor=(1,0.5))
#1.一些初始的状态和变量的赋值
motion_var= 1.0#人的运动运动方差
sensor_var= 2.0 #GPS的运动方差
x = gaussian(0,20**2)
velocity = 1.0
dt = 1 #时间单位的最小刻度
motion_model = gaussian(velocity,motion_var)
#2.生成数据
zs = []
current_x = x.mean
for _ in range(10):#我们让小明周10s,每走1s,就看看gps进行矫正并且把这些数据存起来
#先生成我们的运动数据
v = velocity + randn()*motion_var
current_x += v*dt #将上一秒的位移加到这一秒
#生成观测数据
measurement = current_x + randn()*sensor_var#gps观测也有一定误差
zs.append(measurement)
zs
[1.7745837204798636,
0.7238059161348066,
2.2738223282592034,
5.1347547337355195,
5.692724470550488,
5.01630210516077,
7.273752372058138,
10.711965916869577,
8.341629923352198,
10.715059361392347]