基础知识

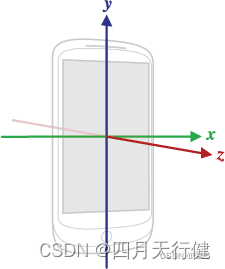
         加速度传感器可以返回x、y、z三轴的加速度数值，该数值受地心引力的影响。

        将手机平放桌面上，x、y、z轴默认为9.81；手机向下z轴为-9.81。

        将手机向左倾斜，x轴为正，向右倾斜，x为负；

         将手机向上倾斜，y轴为负，向下倾斜，x为正。

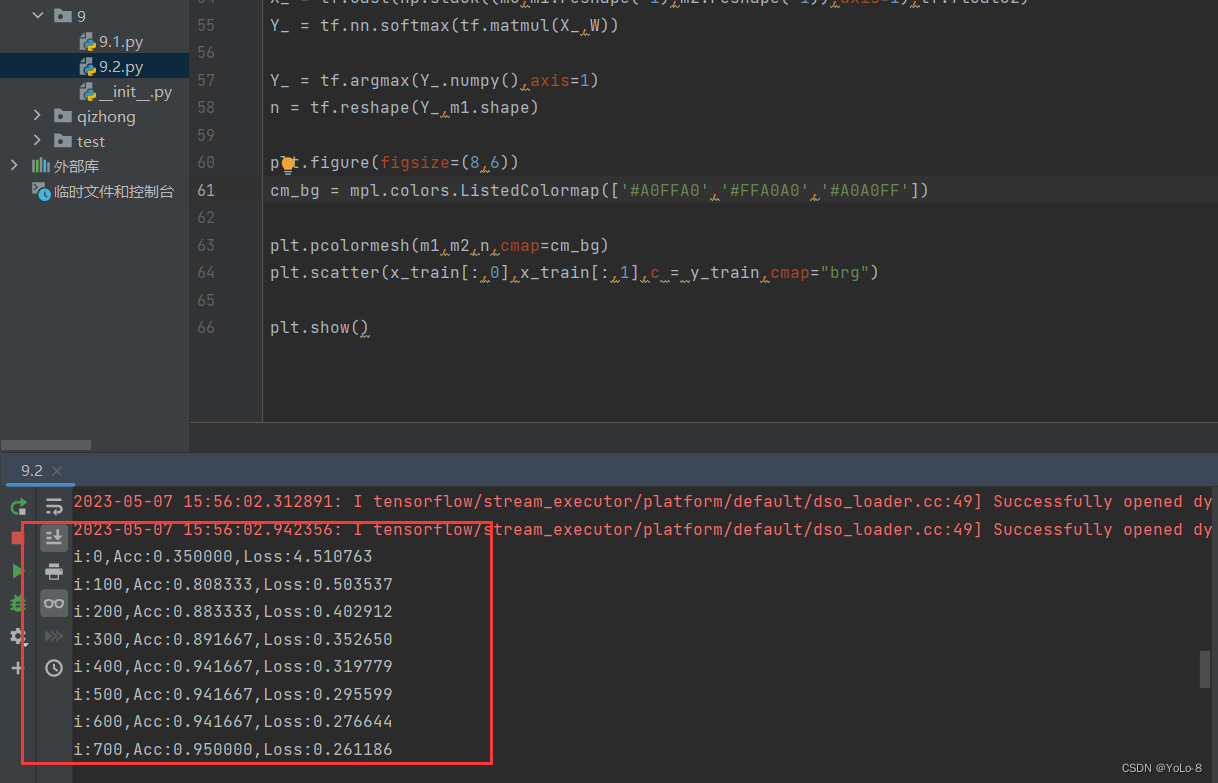
如下图上到下依次为xyz轴数值，可知手机状态是向右倾斜的。

实践使用

新建项目，修改布局文件activity_main.xml,代码如下：

<?xml version="1.0" encoding="utf-8"?>
<LinearLayout xmlns:android="http://schemas.android.com/apk/res/android"
    android:orientation="vertical"
    android:layout_width="match_parent"
    android:layout_height="match_parent">

    <TextView
        android:id="@+id/textViewx"
        android:layout_width="wrap_content"
        android:layout_height="wrap_content" />

    <TextView
        android:id="@+id/textViewy"
        android:layout_width="wrap_content"
        android:layout_height="wrap_content" />

    <TextView
        android:id="@+id/textViewz"
        android:layout_width="wrap_content"
        android:layout_height="wrap_content" />

</LinearLayout>

修改MainActivity代码如下：

public class MainActivity extends AppCompatActivity implements SensorEventListener {
    private SensorManager sm;
    TextView textViewx;
    TextView textViewy;
    TextView textViewz;
    @Override
    protected void onCreate(Bundle savedInstanceState) {
        super.onCreate(savedInstanceState);
        setContentView(R.layout.activity_main);
        textViewx = (TextView) findViewById(R.id.textViewx);
        textViewy = (TextView) findViewById(R.id.textViewy);
        textViewz = (TextView) findViewById(R.id.textViewz);

//        获取传感器管理器
        sm = (SensorManager) getSystemService(SENSOR_SERVICE);
//        调用方法获取需要的传感器
        Sensor mSensorOrientation = sm.getDefaultSensor(Sensor.TYPE_ACCELEROMETER);
//        注册监听器
//SENSOR_DELAY_FASTEST最灵敏

//SENSOR_DELAY_GAME 游戏的时候，不过一般用这个就够了

//SENSOR_DELAY_NORMAL 比较慢。

//SENSOR_DELAY_UI 最慢的
        sm.registerListener(this, mSensorOrientation, android.hardware.SensorManager.SENSOR_DELAY_UI);

    }
//      该方法在传感器的值发生变化的时候调用
    @Override
    public void onSensorChanged(SensorEvent event) {
        float X = event.values[0];
        float Y = event.values[1];
        float Z = event.values[2];
        textViewx.setText(X+"");
        textViewy.setText(Y+"");
        textViewz.setText(Z+"");
    }
//    当传感器的进度发生改变时回调，sensor是传感器对象,accuracy是传感器新的精度
    @Override
    public void onAccuracyChanged(Sensor sensor, int accuracy) {
    }
//  在activity变为不可见的时候，传感器依然在工作，这样很耗电，所以我们根据需求可以在onPause方法里面停掉传感器的工作
    @Override
    public void onPause() {
//        取消监听器的注册
        sm. unregisterListener(this);
        super.onPause();
    }
}

在手机上运行你会发现三个数值小数部分一直在变化，这是正常的。