来源：力扣（LeetCode）

描述：

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

• 1 <= fruits.length <= 10⁵
• fruits[i].length == 2
• 0 <= startPos, positioni <= 2 * 10⁵
• 对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
• 1 <= amounti <= 10⁴
• 0 <= k <= 2 * 10⁵

方法一：二分查找

思路与算法

由于题目中的水果位置已经是升序排列，假设此时我们知道在 x 轴上的移动区间为 [left, right]，则可利用二分查找很快计算出区间 [left, right] 范围内摘掉水果的数目。题目的关键则转变为求从起点移动 k 步而实际在 x 轴上移动的最大区间范围。当然在实际移动过程中肯定优先遵循「贪心」原则，因为这样每个位置的水果只能摘取一次，因此尽可能的移动更远，实际移动方法如下：

• 要么一直往一个方向移动 k 步；要么先往一个方向移动 x 步，然后再反方向移动 k − x 步；
• 实际当 x = 0 时，则一直往一个方向移动 k 步；

根据以上分析，由于有左右两个方向，我们通过不断枚举 x，此时 x ∈ [0, $\frac{k}{2}$]，即可求出其移动的区间。假设我们从起点 startPos 出发，实际有以下两种情况：

• 先往左移动 x 步，然后向右移动 k − x 步，此时的移动区间范围 [startPos − x, startPos + k − 2x]；
• 先往右移动 x 步，然后向右移动 k − x 步，此时的移动区间范围 [startPos + 2x − k, startPos + x]；

假设已知道当前采摘人员在 x 轴上的移动区间范围，则我们利用二分查找即可在 O(logn) 时间复杂度内找到区间中包含的水果的数量，实际可以用前缀和进行预处理即可。

代码：

class Solution {
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        int n = fruits.size();
        vector<int> sum(n + 1);
        vector<int> indices(n);
        for (int i = 0; i < n; i++) {
            sum[i + 1] = sum[i] + fruits[i][1];
            indices[i] = fruits[i][0];
        }
        int ans = 0;
        for (int x = 0; x <= k / 2; x++) {
            /* 向左走 x 步，再向右走 k - x 步 */
            int y = k - 2 * x;
            int left = startPos - x;
            int right = startPos + y;
            int start = lower_bound(indices.begin(), indices.end(), left) - indices.begin();
            int end = upper_bound(indices.begin(), indices.end(), right) - indices.begin();
            ans = max(ans, sum[end] - sum[start]);
            /* 向右走 x 步，再向左走 k - x 步 */
            y = k - 2 * x;
            left = startPos - y;
            right = startPos + x;
            start = lower_bound(indices.begin(), indices.end(), left) - indices.begin();
            end = upper_bound(indices.begin(), indices.end(), right) - indices.begin();
            ans = max(ans, sum[end] - sum[start]);
        }
        return ans;
    }
};

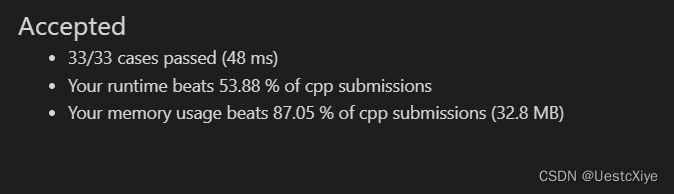
执行用时：584 ms, 在所有 C++ 提交中击败了37.93%的用户
内存消耗：120.9 MB, 在所有 C++ 提交中击败了53.45%的用户
复杂度分析
时间复杂度：O(n + klogn)，其中 n 表示数组的长度，k 表示给定的整数 k。计算数组的前缀和需要的时间为 O(n)，每次查询区间中的水果数量时需要的时间为 O(logn)，一共最多有 k 次查询，因此总的时间复杂度即为 n + klogn。
空间复杂度：O(n)，其中 n 表示数组的长度。计算并存储数组的前缀和，需要的空间为 O(n)。

方法二：滑动窗口

思路与算法

我们可以换个思路来思考该问题，假设已知区间 [left, right]，现在从起点 startPos 出发，至少需要走多少步才能遍历该区间，实际我们可以看到分为以下三种情况：

• 当 startPos > right 时，即区间在 startPos 的左边，此时应该从起点开始一直向左移动，直到 left 为止，此时至少需要移动 startPos − left 步；
• 当 startPos < left 时，即区间在 startPos 的右边，此时应该从起点开始一直向右移动，直到 right 为止，此时至少需要移动 right − startPos 步；
• 当 left ≤ startPos ≤ right 时，即 startPos 刚好在区间范围内，此时有两种选择：
  • 从起点开始一直向左移动，直到 left 为止，然后再向右移动到 right，此时需要移动 startPos − left + right − left 步；
  • 从起点开始一直向右移动，直到 right 为止，然后再向左移动到 left，此时最少需要移动 right − startPos + right − left 步；
  • 根据两种情形，最少需要移动 right − left + min(∣right − startPos∣, ∣startPos − left∣) 步;
• 当然上述所有的情形都可以合并为一个计算公式，即实际最少需要移动 right − left + min(∣right − startPos∣, ∣startPos − left∣) 步，才能覆盖区间 [left, right]，如下图所示：
  

我们设函数 step(left, right) 表示从起点 startPos 出发可以覆盖区间 [left, right] 的最少移动步数，此时 step(left,right) = right − left + min(∣right − startPos∣, ∣startPos − left∣)。当固定 right 时，此时减少 left，可以观察到:

• 当 left < startPos 时，step(left − 1, right) < step(left, right);
• 当 left ≥ startPos 时，step(left − 1, right) = step(left, right);

综上可以得到结论：

step(left − 1, right) ≤ step(left, right)
即随着 left 的减小，step(left, right) 可能会减小，但一定不会继续增大，利用这个特性我们即可利用滑动窗口来遍历所有符合要求的最大区间，然后找到区间内的覆盖水果的最大值即可，实际计算过程如下:

• 初始时 left = 0, right = 0，每次 right 向右移动一步；
• 计算当前区间 [left, right] 需要的移动步数 step，假设 step > k，则我们移动左起点 left，直达满足 step < k, left ≤ right，即可求出移动步数小于等于 k 且以 right 为终点的最长区间，计算出改区间覆盖的水果数目即可；
• 依次按照上述方式移动直到 right 移动到终点为止。

代码：

class Solution {
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        int left = 0;
        int right = 0;
        int n = fruits.size();
        int sum = 0;
        int ans = 0;

        auto step = [&](int left, int right) -> int {
            if (fruits[right][0] <= startPos) {
                return startPos - fruits[left][0];
            } else if (fruits[left][0] >= startPos) {
                return fruits[right][0] - startPos;
            } else {
                return min(abs(startPos - fruits[right][0]), abs(startPos - fruits[left][0])) + \
                       fruits[right][0] - fruits[left][0];
            }
        };
        // 每次固定住窗口右边界
        while (right < n) {
            sum += fruits[right][1];
            // 移动左边界
            while (left <= right && step(left, right) > k) {
                sum -= fruits[left][1];
                left++;
            }
            ans = max(ans, sum);
            right++;
        }
        return ans;
    }
};

执行用时：316 ms, 在所有 C++ 提交中击败了81.03%的用户
内存消耗：117.3 MB, 在所有 C++ 提交中击败了75.86%的用户
复杂度分析
时间复杂度：O(n)，其中 n 表示数组的长度。每次固定窗口的右侧，然后尝试移动左侧窗口，右侧端点最多移动 n 次，左侧端点最多移动 n 次，因此时间复杂度为 O(2n) = O(n)。
空间复杂度：O(1)。
author：LeetCode-Solution