目录
- 链表的回文结构
- 相交链表
- 环形链表I
- 环形链表II
链表的回文结构
链接: link
题目描述:

题目思路:
本题思路是找到每一条链表的中间节点,之后逆置中间节点之后的链表,定义两个指针,分别指向逆置后链表的头部的链表的中间节点,依次进行比对,如果比对过程中两个节点的值不相等则返回false,比对结束后证明该链表是回文结构,返回true。
步骤1:找到链表的中间节点
方法:快慢指针,slow和fast指针
情况1:链表节点个数为偶数个,slow一次走一步,fast一次走两步,结束条件是fast为空,则slow指向的则是要找的mid节点。
情况2:链表节点个数为奇数个,slow一次走一步,fast一次走两步,结束条件是fast->next为空,则slow指向的则是要找的mid节点。
步骤2:逆置链表中间节点后的节点
方法:方法1思路:
这力我们需要三个指针n1 n2 n3方便我们进行迭代
初始化n1指向NULL,n2指向第一个节点,n3指向第2个节点,下面是n1 n2 n3 3个指针移动的过程。
1、改变第一个指针n1的指向,链表反转后,第一个节点的指针域指向的是NULL,就上图来看,也就是n2->next=n1;
2、改变指向后,我们接下来的操作就是移动3个指针继续进行链接变向的操作。下面是如何变动三个指针的过程:
将n2的值赋给n1,n3的值赋给n2,n3再向下走一步。
3、下面进行的步骤就是反转链接方向:n2->next = n1。
上述过程就是我们反转的最核心步骤,下面是本题循环终止条件和Bug点:
这里我们要注意,本题要清楚的是,当n1指向最后一个节点的时候,循环就终止了,但是这个点并不是我们所需要的循环的终止条件,循环终止条件是n2为空指针。
本题大致雏形就出来了,但是我们实际进行运行的时候,还会出现空指针的问题,问题的来源就在于n3。
当n2不为空指针,并且n2此时已经指向最后一个节点时,n3已经为空指针,当n2为空指针的时候,n3也要向下走,这就造成了空指针的问题,所以我们要进行处理的是n3,n3不为空指针的时候,n3才可以继续向下走。
最后状态如下图所示:最后我们只需要返回n1就可以了
疑问点:
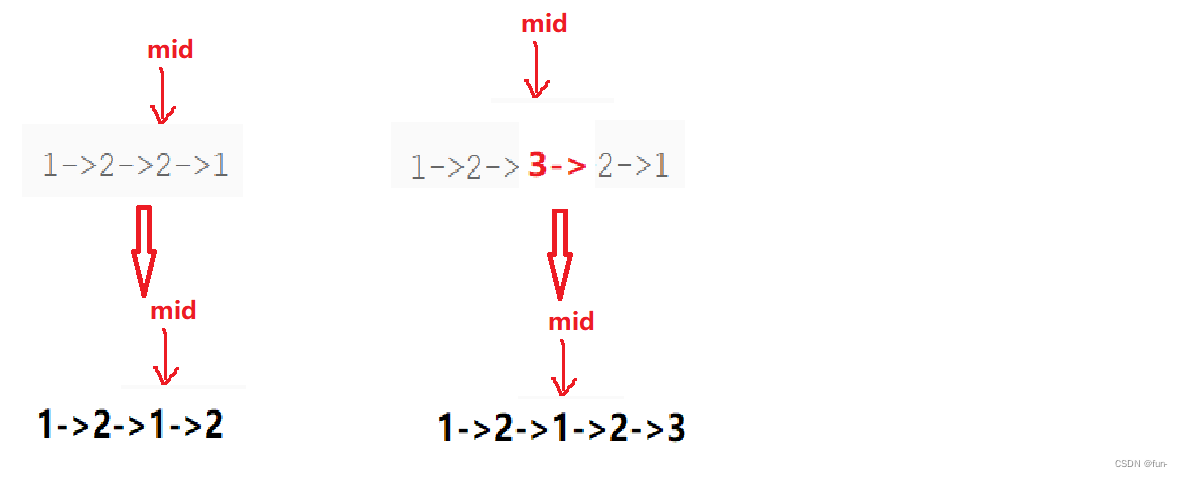
偶数个节点循环终止的条件是当mid节点为空,也就是下面情况:

但是奇数节点就会出现下面的情况:

这里我们只要记住虽然我们逆置了mid之后的链表,但是我们并没有改变2节点之后链接的是3节点,所以这里我们不用进行处理,继续让两个指针向下走,直到mid指向空,循环结束。
代码实现:
struct ListNode* reverseList(struct ListNode* head) {
if(head == NULL || head->next == NULL)
return head;
struct ListNode* n1, *n2, *n3;
n1 = head;
n2 = n1->next;
n3 = n2->next;
n1->next = NULL;
//中间节点不为空,继续修改指向
while(n2)
{
//中间节点指向反转
n2->next = n1;
//更新三个连续的节点
n1 = n2;
n2 = n3;
if(n3)
n3 = n3->next;
}
//返回新的头
return n1;
}
struct ListNode* middleNode(struct ListNode* head){
struct ListNode* slow = head;
struct ListNode* fast = head;
while(fast!=NULL && fast->next != NULL)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
class PalindromeList {
public:
bool chkPalindrome(ListNode* A) {
struct ListNode* mid = middleNode(A);
struct ListNode* rmid = reverseList(mid);
struct ListNode* head = A;
while(rmid)
{
if(head->val!=rmid->val)
{
return false;
}
else
{
head = head->next;
rmid = rmid->next;
}
}
return true;
}
};
相交链表
链接: link
题目描述:





题目思路:
本题首先要明确下图的相交是绝对不会出现的:

解释:因为上图中相交节点没有两个指针域,所以说一旦两条链表相交,那么必然是下图情况:

判断两条链表相交的方法:
两条链表尾指针相等(这里是尾指针并不是尾节点值相等),如果尾指针相等,则证明两条链表相交,那么接下来的步骤就是求交点,如果尾指针不相等,则返回NULL。
如何求交点:
这里我们要明确,一旦到求交点这步,就证明一定会有交点,因为无交点的情况已经返回NULL。
这里仍然是一个快慢指针的问题,因为两条链表长度不相同,所以无法在求交点的时候指向同一个节点,这时就需要调整快慢指针,在调整快慢指针之前先求出两条链表的长度lenA和lenB,让长链表的指针先走(lenA-lenB)步,再两个指针同时出发,判断两指针地址是否相等,相等则返回。
1、求两条链表节点个数:循环结束条件tailA->next=NULL****tailB->next=NULL,lenA和lenB初始值为1
2、这里为了减少本题代码冗余,在求出abs(lenA-lenB)(abs是库函数,用abs求出的值是该数的绝对值)之前首先定义两个结构体指针longList和shortList,假设第一条链表长度是最长的,两指针赋初值longList = headA,shortList=headB,判断如果lenB>lenA,则更改初值longList = headB,shortList=headA,这里的目的是减少代码冗余。
让longList先走abs(lenA-lenB)步:
此时两指针同时向下移动,判断两指针地址是否相等(循环条件),相等则返回longList(shortList)。
代码实现:
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
//判断链表当中是否存在相交节点,如何判断相交?尾指针地址相同。
struct ListNode* tailA=headA;
struct ListNode* tailB=headB;
int lenA =1;
int lenB =1;
while(tailA->next)
{
tailA=tailA->next;
lenA++;
}
while(tailB->next)
{
tailB=tailB->next;
lenB++;
}
if(tailA!=tailB)
{
return NULL;//说明不存在相交节点
}
//下面是存在相交节点并且求相交节点过程
int gap = abs(lenA-lenB);
struct ListNode* longList=headA;
struct ListNode* shortList=headB;
if(lenA<lenB)
{
longList=headB;
shortList=headA;
}
while(gap--)
{
longList=longList->next;
}
while(longList!=shortList)
{
longList=longList->next;
shortList=shortList->next;
}
return longList;
}
环形链表I
链接: link
题目描述:
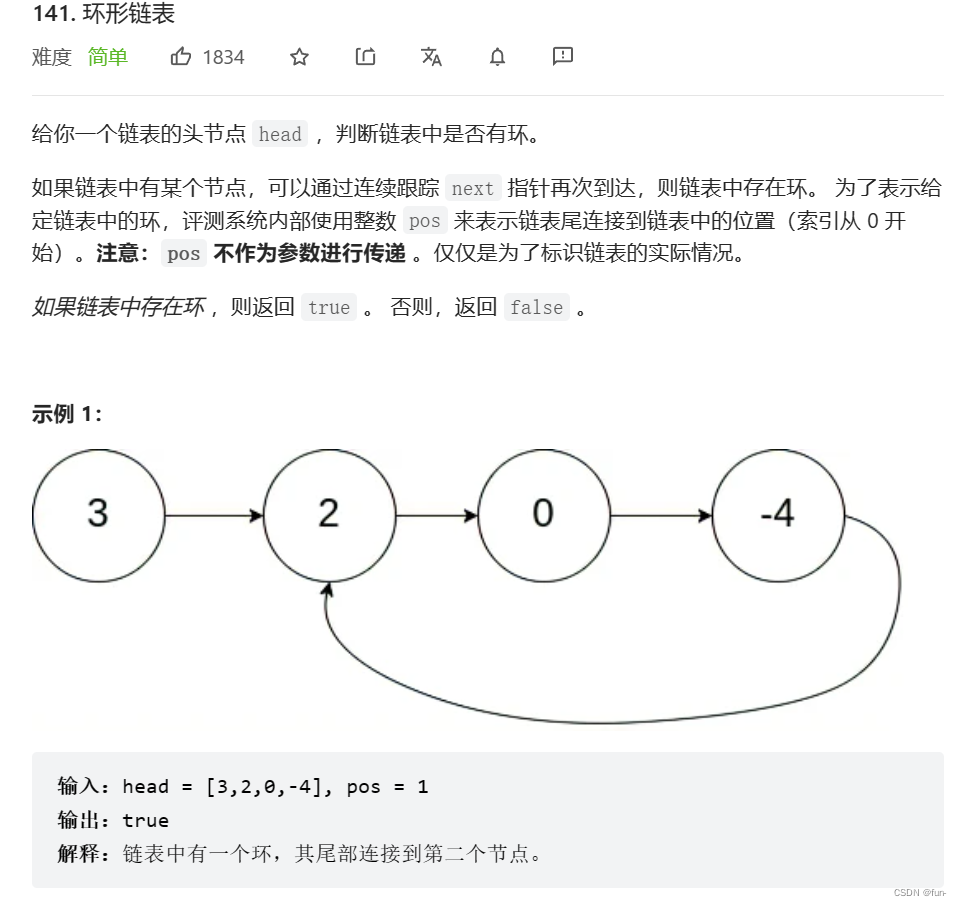
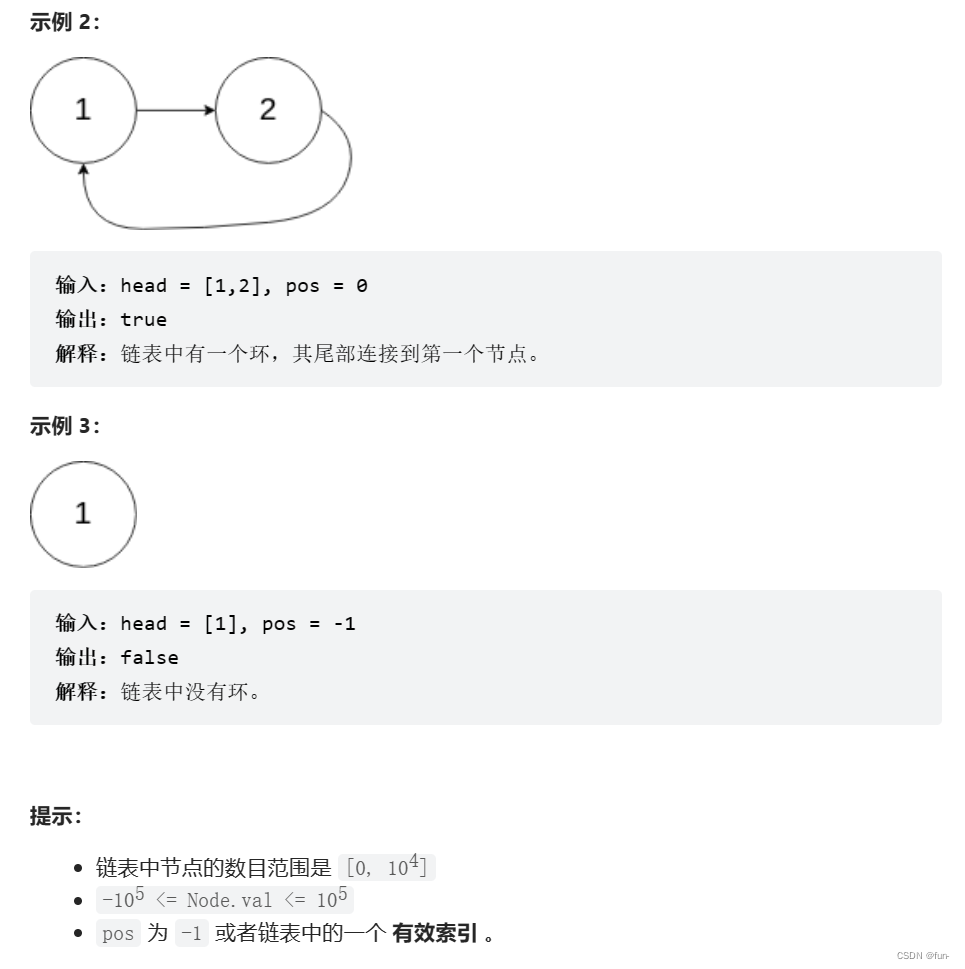
题目思路:
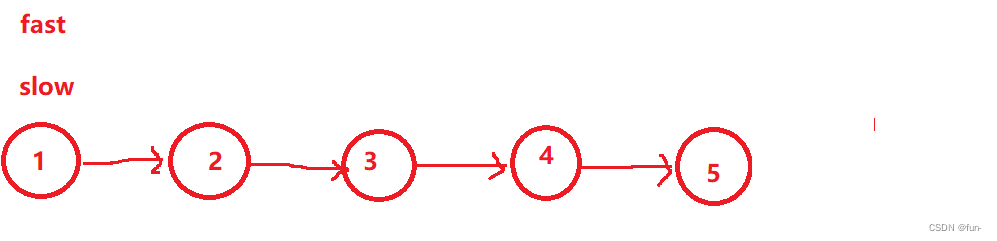
本题题目思路依然是快慢指针,快指针一次走两步,慢指针一次走一步。
情况1:链表中不存在环,奇数个节点,循环结束条件为fast->next = NULL
情况2:链表中不存在环,偶数的节点,循环结束条件为fast=NULL
情况3:链表中存在环,依然是slow指针走一步,fast指针走两步,但是什么情况才能证明链表当中存在环呢?这是一个追击问题,如果链表当中存在环,那么总会有一次,两个指针指向同一个地址,也就是说slow=fast。
大家可以画一下,下图就是追击之后两指针相遇的位置
代码实现:
bool hasCycle(struct ListNode *head)
{
struct ListNode* slow = head;
struct ListNode* fast = head;
while(fast&&fast->next)
{
slow=slow->next;
fast = fast->next->next;
if(slow==fast)
{
return true;
}
}
return false;
}
两个问题:
问题1:slow一次走一步fast 一次走两步,一定会相遇吗?答案是一定会。
fast先进环,slow后进环,fast进环后开始追击slow,slow走1步,fast走两步,他们之间的距离缩小1。假设此时fast和slow的距离为N
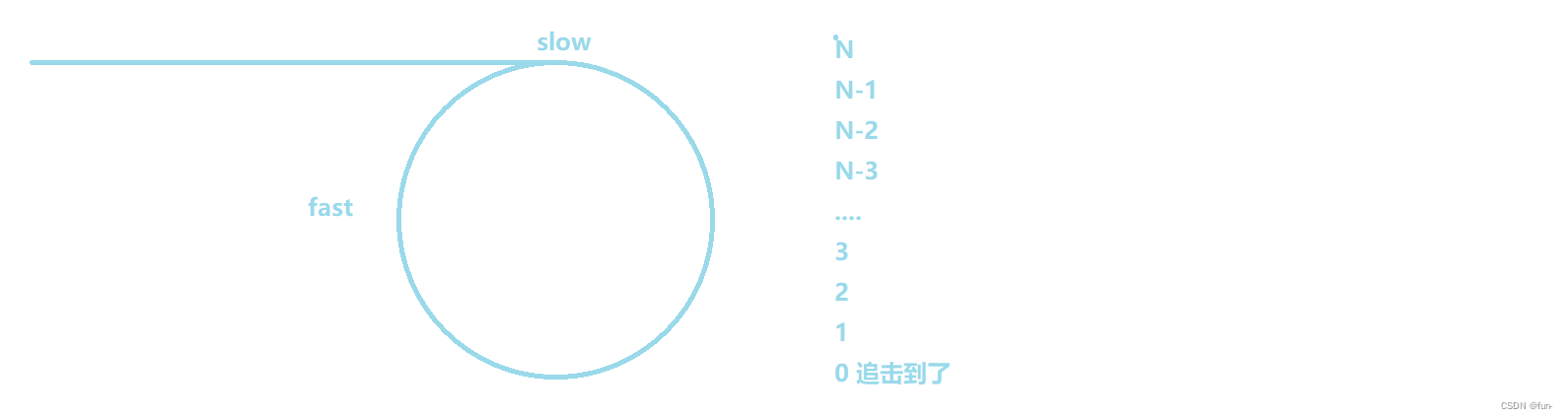
问题2:slow一次走一步fast 一次走三步,一定会相遇吗?答案是不一定会。
fast先进环,slow后进环,fast进环后开始追击slow,slow走1步,fast走3步,他们之间的距离缩小2。
这时是否能追击到取决于fast和slow之间的距离N。

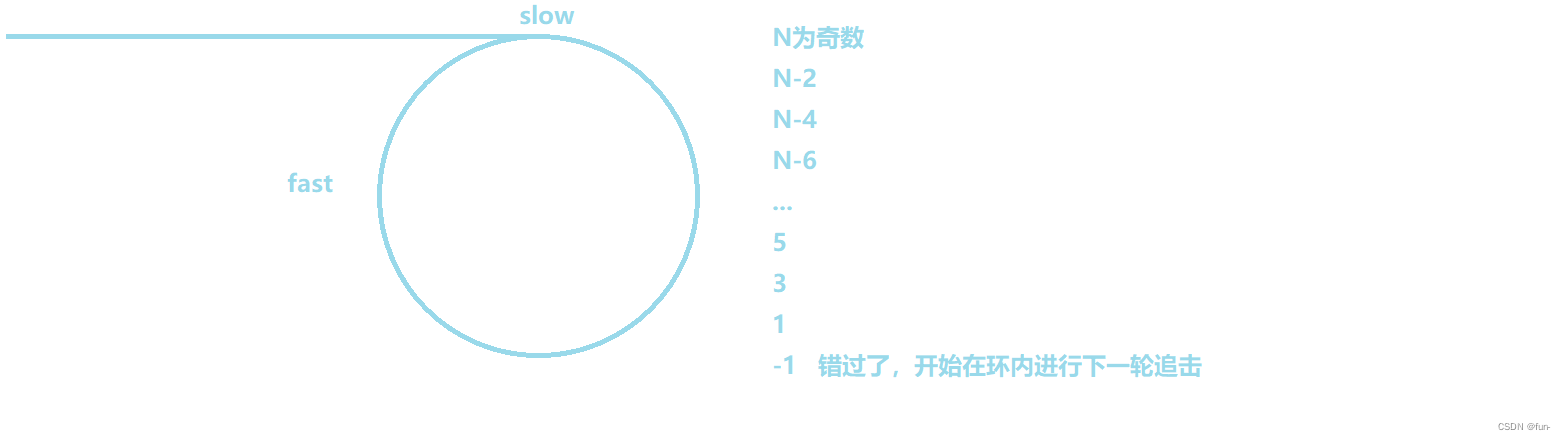
在环内追击时,取决于环内节点的个数C,此时slow和fast的距离是C-1
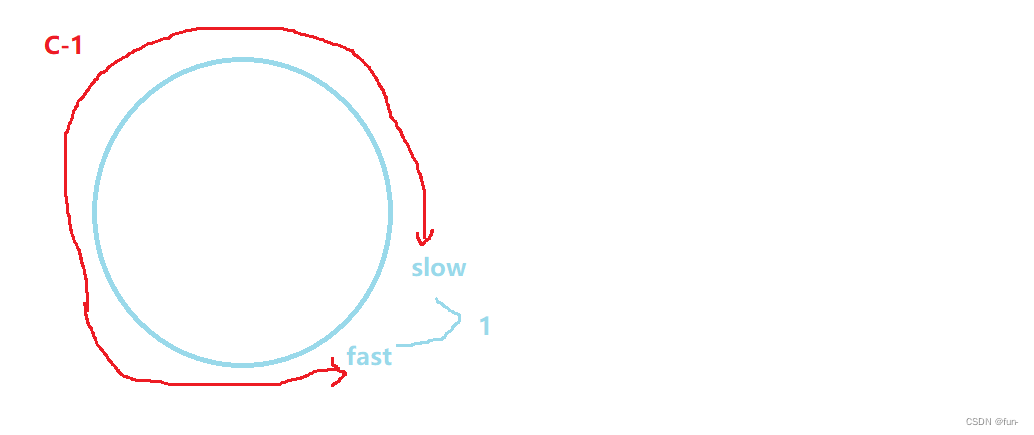
如果C-1为偶数,那么某一时刻,一定会追上。
如果C-1为奇数,那么永远都追不上。
环形链表II
链接: link
题目描述:
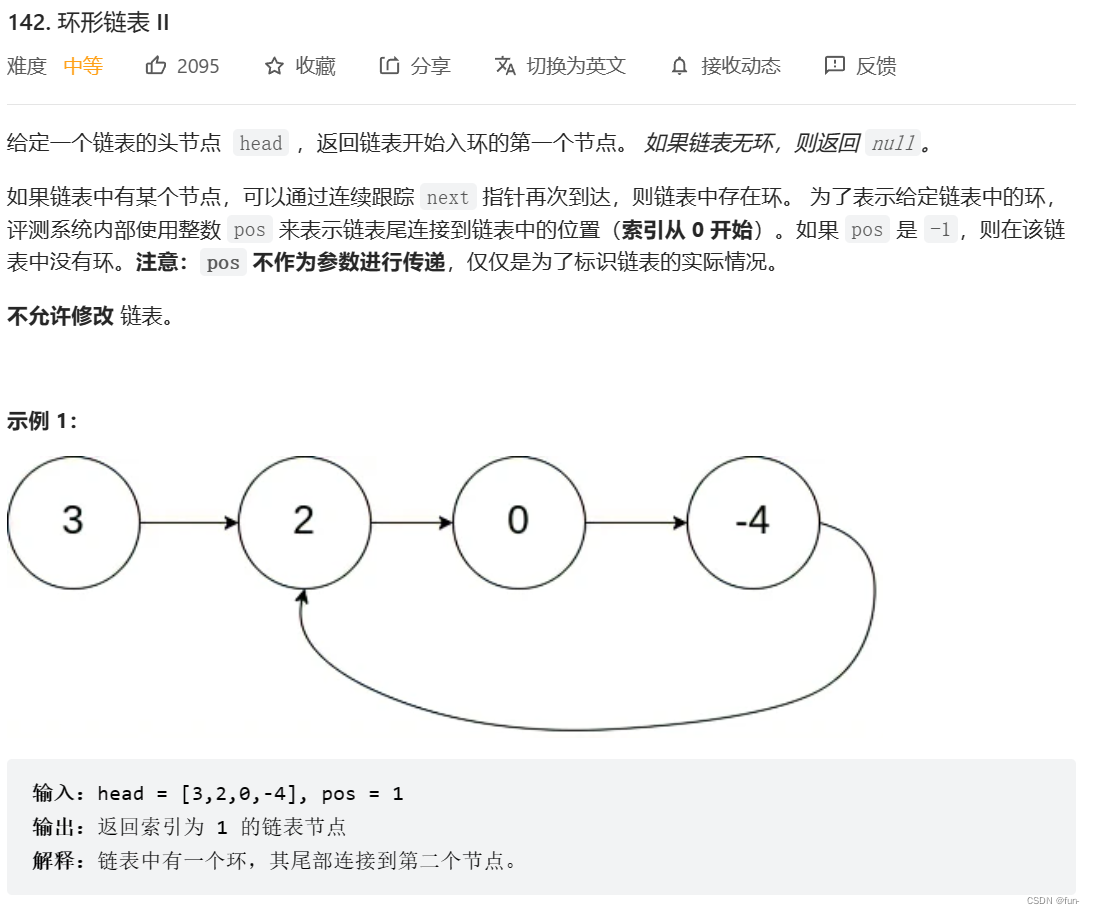

题目思路:
方法1:快慢指针
方法一的主要思路就是:一个指针从相遇点开始走,一个指针从链表头开始走,他们会在入环的第一个节点相遇。
slow一次走一步,fast一次走两步
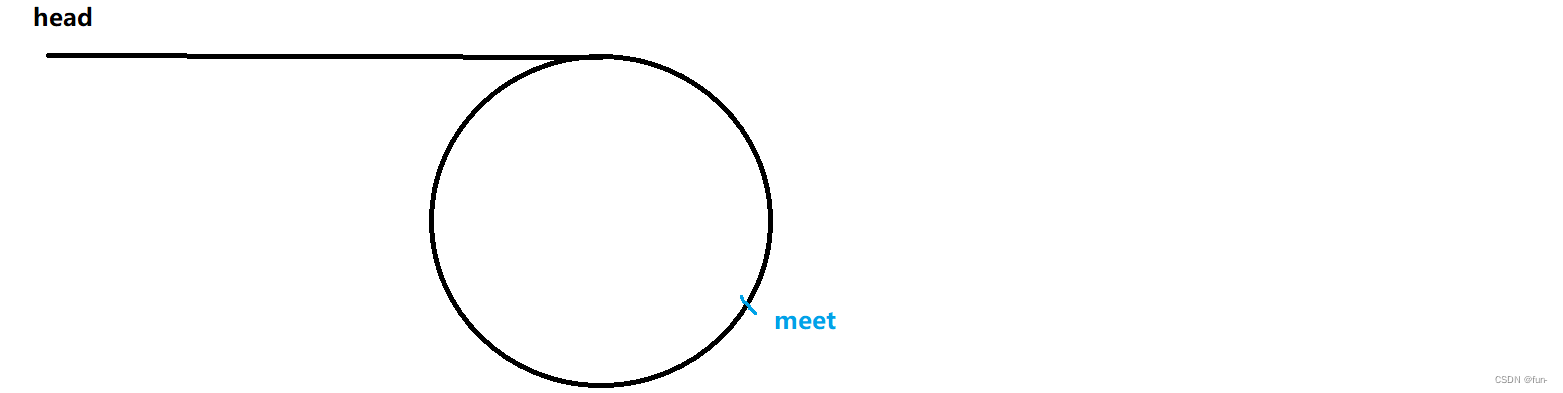
假设下图中meet指针指向的节点为fast和slow指针相遇的节点。
假设
从链表头到入环的第一个节点的长度为L
入环第一个节点到meet的长度为X
环的长度为C
那么到相遇点meet时
slow指针走过的路程为:L+X
fast指针走过的路程为:L+nC-X
而fast一次走两步,slow一次走一步
所以2(L+X)=L+nC-X,所以L=nC-X=(n-1)*C+C-X,仔细观察这个式子,就是本题开头所说的思路:一个指针从头开始走,一直指针从相遇的地方开始在走,他们会在入环的第一个节点相遇。
这里的疑问是:为什么fast指针走过的路程为:L+n*C-X,不是L+C-X
如果L的长度很大,而C的长度很小呢?下图显然不能得到入口点

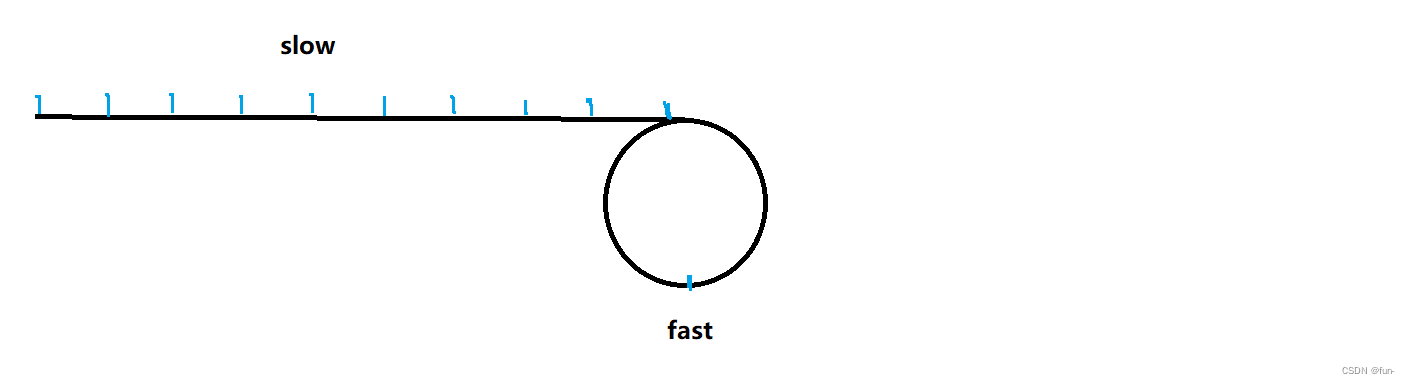
这里举一个例子:假设L长度为10,C的长度为2,slow指针一次走一步,fast指针一次走两步,当fast进环时,slow的位置如下图:
这就是为什么fast走过的路程是L+n*C-X,在slow进到环内之前,fast要先在环内转n(n的值根据具体实际情况推算)圈。
注意:本题slow和fast一定会相遇,不存在slow进环后转了几圈,fast才追上,因为他们之间的距离每次缩小一,slow进环后,slow走一圈,fast都走两圈了,肯定追上了。
代码实现:
struct ListNode *detectCycle(struct ListNode *head)
{
struct ListNode* slow = head;
struct ListNode* fast = head;
while(fast&&fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow==fast)
{
struct ListNode* meet= slow;
while(meet!=head)
{
meet = meet->next;
head = head->next;
}
if(meet==head)
{
return meet;
}
}
}
return NULL;
}
方法2:

代码实现:
struct ListNode *detectCycle(struct ListNode *head)
{
struct ListNode* slow = head;
struct ListNode* fast = head;
int len1 = 1;
int len2 = 1;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)//有环
{
struct ListNode* meet = slow;
struct ListNode* meetnext = meet->next;
meet->next = NULL;
struct ListNode* head1 = head;
struct ListNode* head2 = meetnext;
struct ListNode* tail1 = head1;
struct ListNode* tail2 = head2;
while(tail1->next)
{
tail1 = tail1->next;
len1++;
}
while(tail2->next)
{
tail2 = tail2->next;
len2++;
}
int gap = abs(len1-len2);
struct ListNode* longList = head1;
struct ListNode* shortList = head2;
if(len2>len1)
{
longList=head2;
shortList = head1;
}
while(gap--)
{
longList = longList->next;
}
while(longList!=shortList)
{
longList = longList->next;
shortList=shortList->next;
}
return longList;
}
}
return NULL;
}