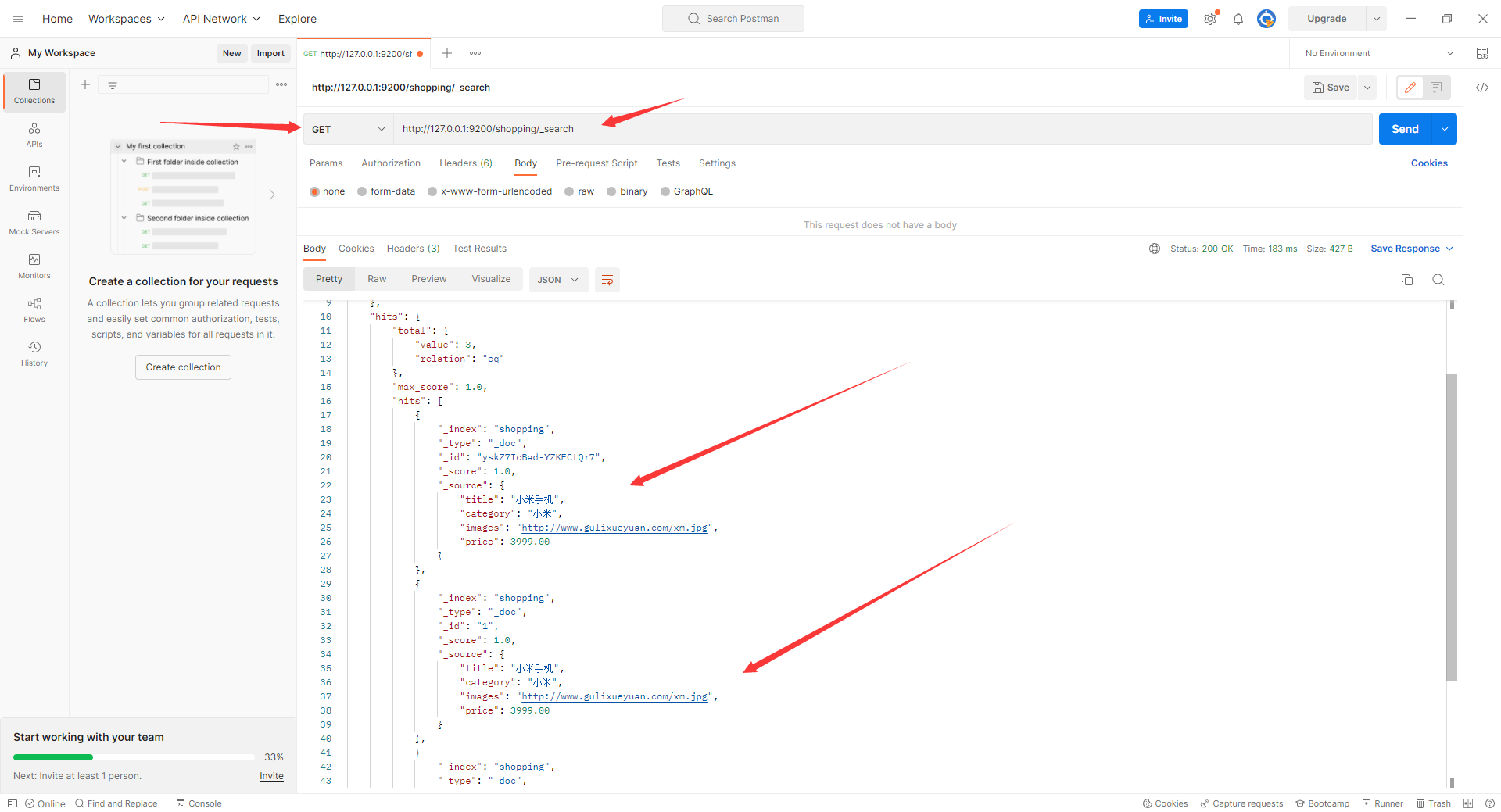
217、存在重复元素(easy)
输入:nums = [1,2,3,1] 输出:true输入:nums = [1,2,3,4] 输出:false输入:nums = [1,1,1,3,3,4,3,2,4,2] 输出:true
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
nums.sort()
j=1
while(j<len(nums)):
if nums[j-1]==nums[j]:
return True
else:
j+=1
return Falseclass Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
nums_pr=set(nums)
if len(nums_pr)!=len(nums):
return True
else :
return False
总结:第二种方法毫无疑问是最优的,牺牲了内存但加快了时间。
第一种是局部算法:(1)用sort()先排序 (2)用while循环(记住设置条件)进行相互两个比较,只要出现一个相等,就能返回。
第二种是全局算法:(1)使用set()函数全部转化为集合(集合是不允许有相同值) (2)比较两个前后长度。
53、最大子数组和(medium)
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
size = len(nums)
pre = 0
res = nums[0]
for i in range(size):
pre = max(nums[i], pre + nums[i])
res = max(res, pre)
return res

总结:总体思路就是 既要与后面num[i]比较大小,也要与前面累加和(边界值为res=num[0])比较大小。
后面:如图所示,他首先需要一个pre,这个值起到的作用是连续相加,然后去与num[i]比较取最大值。所以通过![]() 实现。
实现。
前面:![]()
![]()
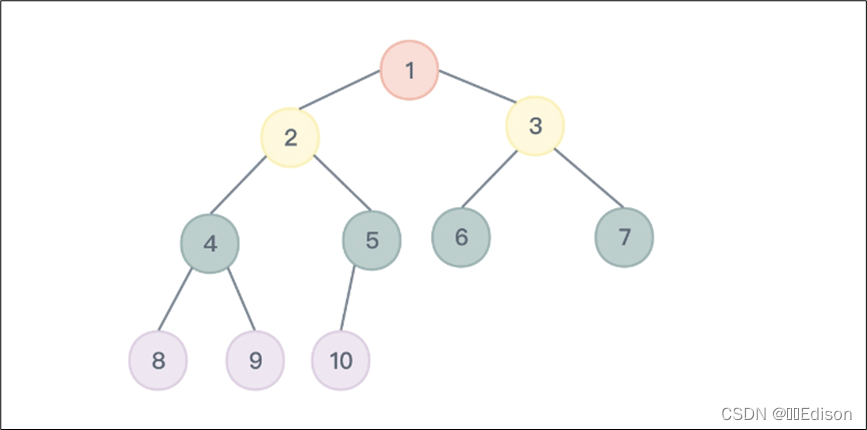
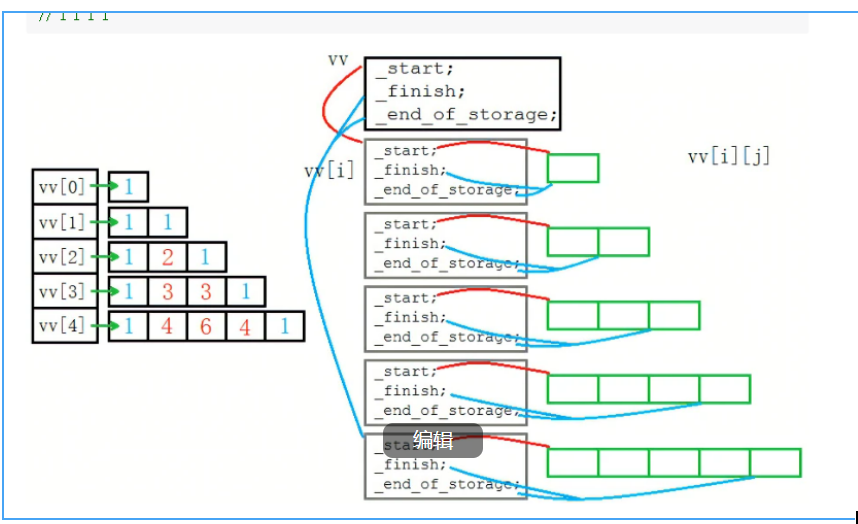
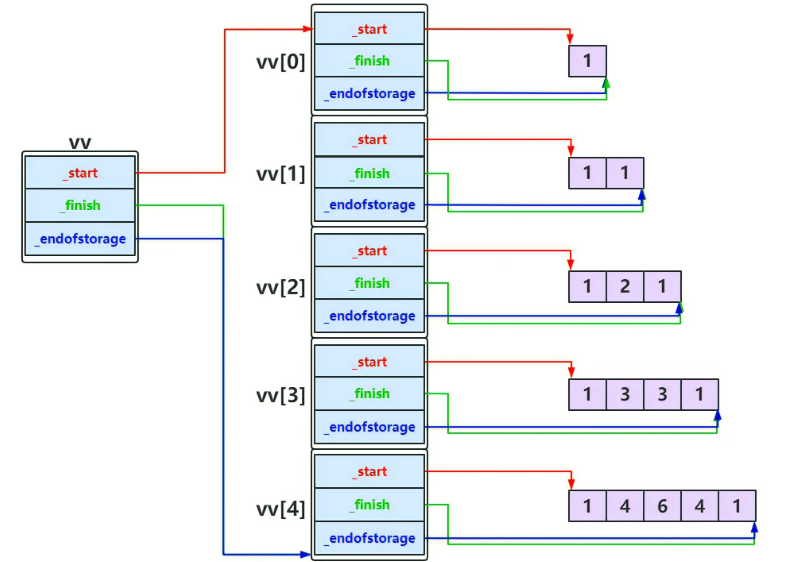
118、杨辉三角(做杨辉三角,首先要懂一些数据存在计算机中的逻辑,我做这道题的时候很多想不通,看了下面图才明白)
 给定一个非负整数
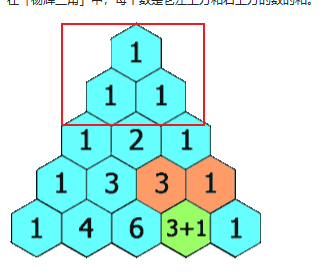
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。在「杨辉三角」中,每个数是它左上方和右上方的数的和。
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
b = list()
for i in range(numRows):
a = list()#此目的是形成一个每行的一个列表
for j in range(i+1):
if j==0 or j==i:#此处不能用while,while满足条件不会动;if 只满足一次就跳出
# a[i][j]=1
a.append(1)
else:
# a[i][j]=a[i-1][j-1]+a[i-1][j]
a.append(b[i-1][j-1]+b[i-1][j])#因为循环,所以已经存在这些值
b.append(a)#此表目的是领导的作用,接收各方面的信息
return b
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
dp = [[1]*(i+1) for i in range(numRows)]
for i in range(2, numRows):
for j in range(1,i):#这里有一个边界条件
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
return dp

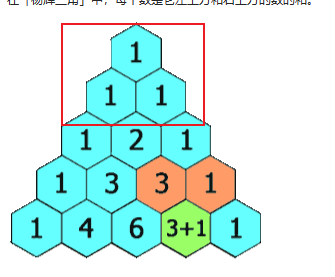

总结:做杨辉三角重点是规律。
规律1:前两层i=0,i=1都是1。
规律2:[i-1][j-1]+[i-1][j] 上一层的第j-1个元素和第j个元素相加。
规律3:第几层就有几个元素。
规律4:j==0或i==j的时候为0
第三种:
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
a = [[1]*(i+1) for i in range(numRows)]
for i in range(numRows):
for j in range(i+1):
if j==0 or j==i:#此处不能用while,while满足条件不会动;if 只满足一次就跳出
a[i][j]=1
else:
a[i][j]=a[i-1][j-1]+a[i-1][j]
return a建议第三种方法,思路简单明了:
只用设置一个参数:a = [[1]*(i+1) for i in range(numRows)]

第二层循环两个互斥条件:
(1)j==0或i==j的时候为0。
(2)a[i][j]=a[i-1][j-1]+a[i-1][j]。
(3)设置好循环边界值。(第三种方法边界值很好设定)
119、杨辉三角||
会做杨辉三角,此题没有任何问题。
class Solution:
def getRow(self, rowIndex: int) -> List[int]:
row=[[1]*(i+1) for i in range(rowIndex+1)]
for i in range(rowIndex+1):
for j in range(i+1):
b=list()
if j==0 or j==i:
row[i][j]=1
else:
row[i][j]=row[i-1][j-1]+row[i-1][j]
return row[rowIndex]509、斐波那济数
方法一(好理解):
class Solution:
def fib(self, n: int) -> int:
num=[0*i for i in range(n+1)]
print(len(num))
#num=[0]*(n+1)
if n==0:
num[0]=0
elif n==1:
num[1]=1
else:
num[0]=0
num[1]=1
for i in range(2,n+1):
num[i]=num[i-1]+num[i-2]
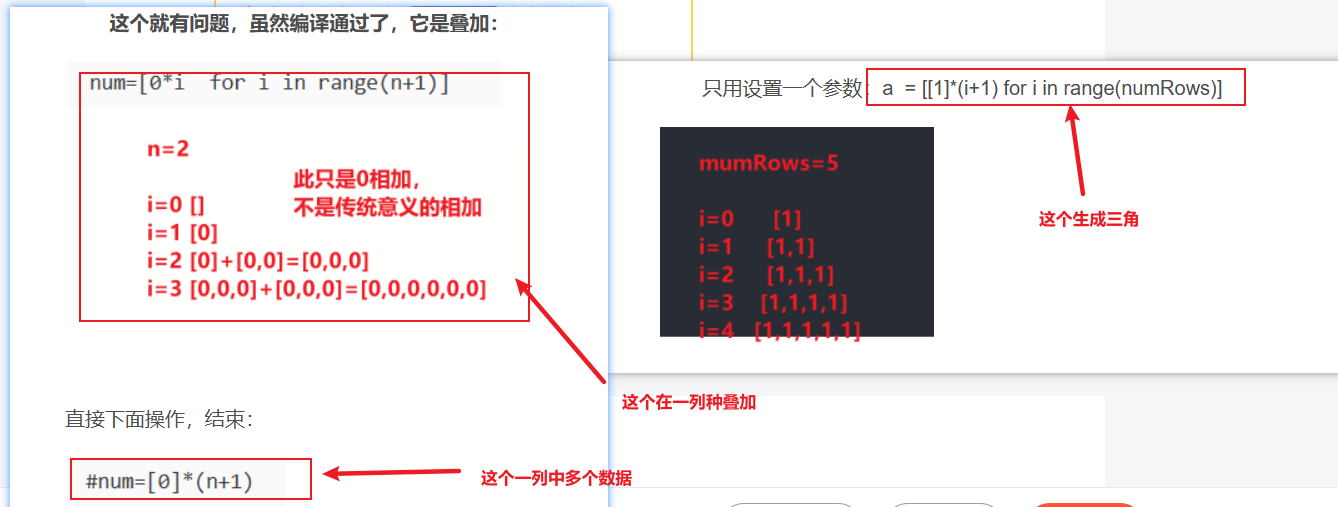
return num[n]这个就有问题,虽然编译通过了,它是叠加:
![]()

直接下面操作,结束:
![]()
方法二(递归):
class Solution:
def fib(self, n: int) -> int:
if n==0:
return 0
elif n==1:
return 1
else:
return self.fib(n-1)+self.fib(n-2)
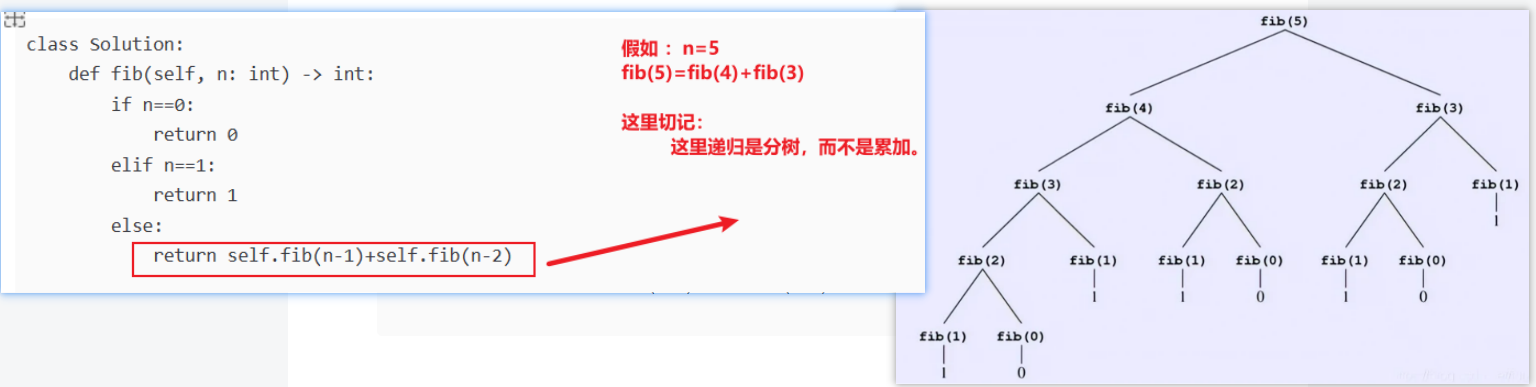
当计算 fib(5) 时,我们共需要计算1次 fib(4),2次 fib(3),3次 fib(2),5次 fib(1) 和3次 fib(0)。这些无意义的重复计算使得递归效率极低。
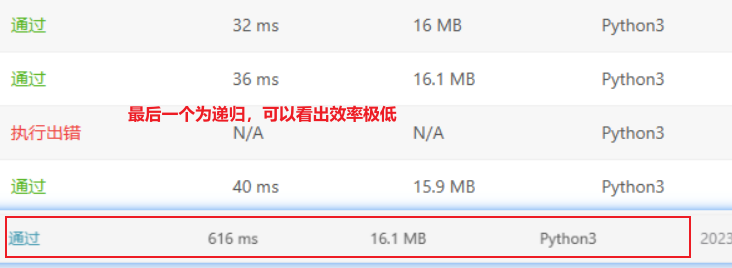
总结:最简单直接就第二种递归,但是时间消耗是真大。
121、买卖股票的最佳时机
给定一个数组 prices,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天买入这只股票,并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
res=prices[0]
deff=0
num=[0]*len(prices)
for i in range(1,len(prices)):
res=min(prices[i],res)
num[i]=max(num[i-1],prices[i]-res)
return num[-1]这道题和(53、最大子数组和)是同种类型的题。
思路:
(1)、res=min(prices[i],res)首先找出比prices[0]大的值,等于或小于prices[0],最后num都会存为0;
(2)、num[i]=max(num[i-1],prices[i]-res) 就和num前面的比找最大的(因为是迭代,所以一直会保存最大的)。
746、使用最小费用爬楼梯(不好理解,真不好理解,但方法不难 ,主要是把cost中的数字都给消耗掉,所以dp长度比cost长)
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
(这道题,我最开始做的时候没看懂,现在看懂了,还是每次爬一个或者两个台阶,那就设置边界值使得cost的值全部用完 )。
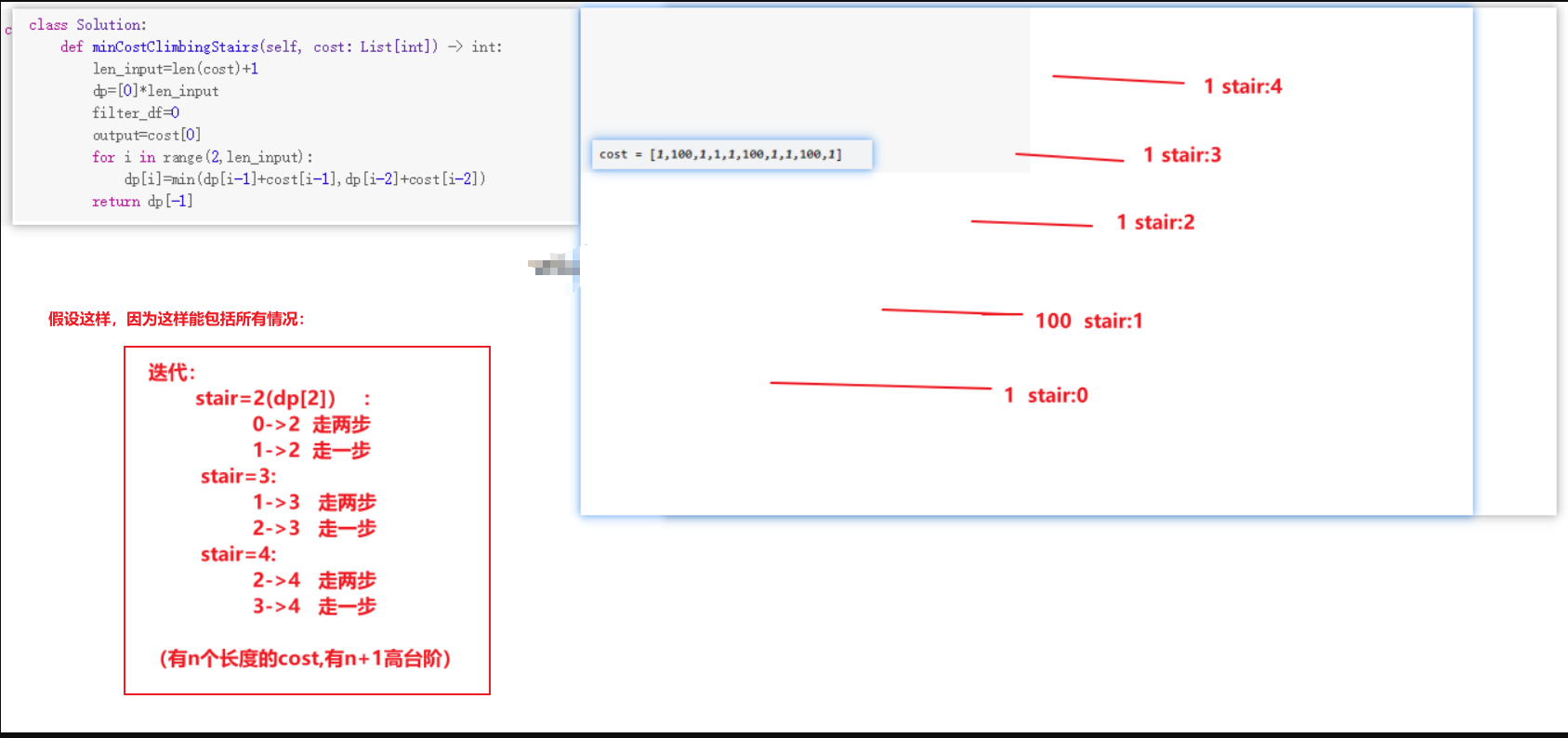
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
length_stair=len(cost)+1
dp=[0]*length_stair
for i in range(2,length_stair):#从最低的参数开始算。
dp[i]=min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1])
return dp[-1]
可以从索引0和索引1开始走,那就让落后的0走两步,让落后的1走一步,这样就包含所有情况。(因为落后的0走一步会包含1的费用,很明显会花费更多)
拔高慢的,打压快的,收集所有情况。
dp[i]=min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1]):最开始i=2时,已设置为0。
dp的长度是比cost的长度多1
剑指Offer 10-11青蛙跳台阶问题
方法1:力扣通不过
class Solution:
def numWays(self, n: int) -> int:
if n==0:
return 1
elif n==1:
return 1
elif n==2:
return 2
else:
return self.numWays(n-1)+self.numWays(n-2)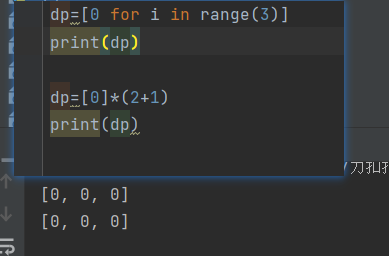
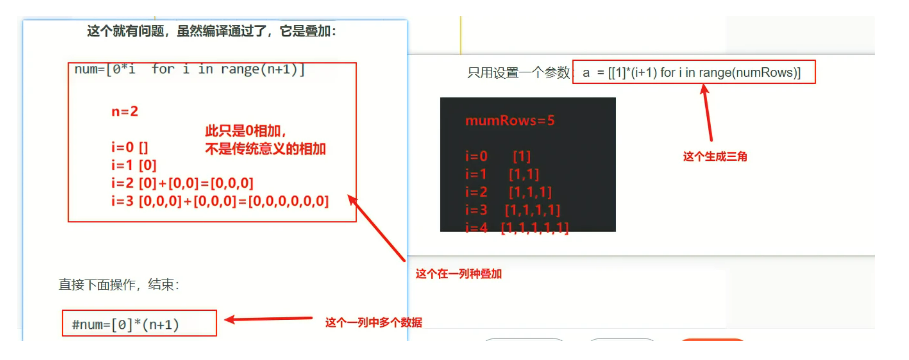

方法2_动态规划 dp[i]为第i个台阶(帮助理解):
class Solution:
def numWays(self, n: int) -> int:
if n==0:
return 1
elif n==1:
return 1
elif n==2:
return 2
else:
dp=[0]*(n+1)
dp=[0 for i in range(n+1)]
dp[0]=1
dp[1]=1
dp[2]=2
for i in range(2,n+1):
dp[i]=dp[i-1]+dp[i-2]
return dp[-1]%(1000000007)重点:dp[i]为第i个台阶(帮助理解)
70、爬楼梯
动态规划:
class Solution:
def climbStairs(self, n: int) -> int:
if n==1:
return 1
elif n==2:
return 2
else:
dp=[0]*(n+1)
dp[0]=1
dp[1]=1
dp[2]=2
for i in range(2,len(dp)):
dp[i]=dp[i-1]+dp[i-2]
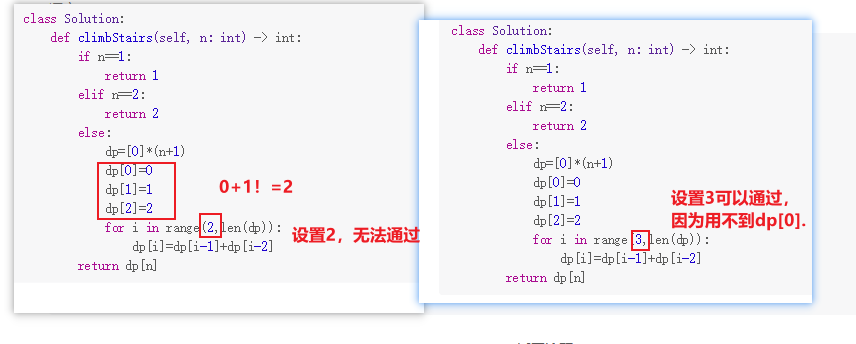
return dp[n]动态规划题:此题切记0台阶也要设置1,要不然用动态规划有问题。
628、三个数的最大乘积
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
class Solution:
def maximumProduct(self, nums: List[int]) -> int:
nums.sort()
rr=nums[-1]*nums[-2]*nums[-3]
td=nums[0]*nums[1]*nums[-1]
if rr <td :
return td
else:
return rr
调用函数:
class Solution:
def maximumProduct(self, nums: List[int]) -> int:
nums.sort()
max_dd=max(nums[0]*nums[1]*nums[-1],nums[-1]*nums[-2]*nums[-3])
return max_dd
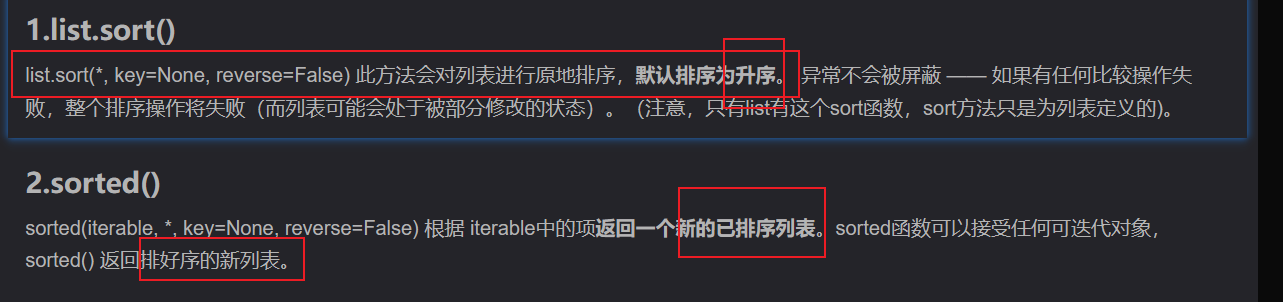
sort()和sorted()区别:
1528、重新排列字符串
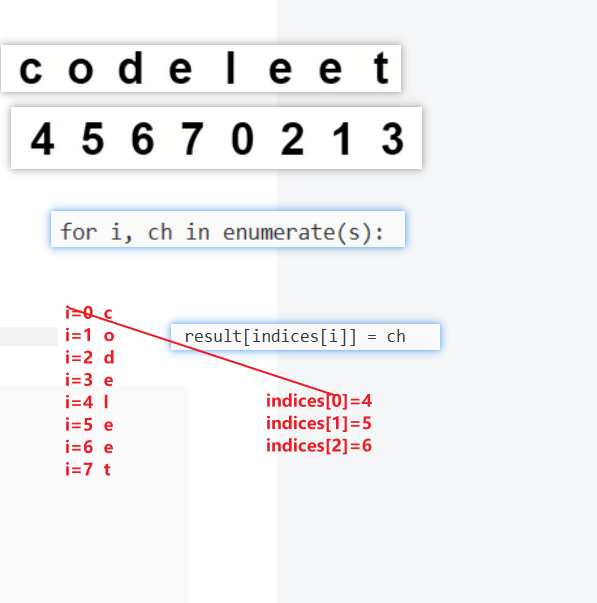
给你一个字符串 s 和一个 长度相同 的整数数组 indices 。请你重新排列字符串 s ,其中第 i 个字符需要移动到 indices[i] 指示的位置。返回重新排列后的字符串。

class Solution:
def restoreString(self, s: str, indices: List[int]) -> str:
length = len(s)
result = [""] * length
for i, ch in enumerate(s):
result[indices[i]] = ch
return "".join(result)
enumerate()函数不会用。