1. 实验目的
①掌握TensorFlow的可训练变量和自动求导机制
②能够使用TensorFlow实现梯度下降法,求解一元和多元线性回归问题
2. 实验内容
下载波士顿房价数据集,使用线性回归模型实现对波士顿房价的预测,并以可视化的形式输出模型训练的过程和结果。
3.实验过程
题目一:
下载波士顿房价数据集,使用属性“低收入人口比例”,训练一元线性回归模型,并测试其性能,以可视化的形式展现训练和测试的过程及结果。
要求:
(1)编写代码实现上述功能;
(2)尝试调试超参数,使模型达到最优的性能,请记录超参数的调试过程,并简要分析和总结;
(3)在程序中增加适当的代码,使其能够计算并记录模型训练时间。
提示:
(1)仅记录训练模型所需的时间,而不是程序运行的总时间
(2)记录程序段运行时间的方法:
import time #导入Time库
start=time.clock() #记录程序起始时间
... #需要记录时间的程序段
end=time.clock() #记录程序结束时间
print(“程序执行时间:”,end-start)
实验代码:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import time
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' #你的 CPU 支持AVX2 FMA(加速CPU计算),但安装的 TensorFlow 版本不支持 解决、
start=time.process_time()
boston_housing = tf.keras.datasets.boston_housing
(train_x,train_y),(test_x,test_y) = boston_housing.load_data() #导入训练集和测试集数据
x_train = train_x[:,12] #使用低收入人口比例
y_train = train_y
x_test = test_x[:,12]
y_test = test_y
learn_rate = 0.009
iter = 1000
display_step =20#设置超参数
#设置模型得参数初始值
np.random.seed(612)
w = tf.Variable(np.random.randn())
b = tf.Variable(np.random.randn())
mse_train = [] #记录训练集上的损失 误差
mse_test = [] #记录测试集上的损失
for i in range(0,iter+1):
with tf.GradientTape() as tape: #梯度带对象的with语句,实现对w和b的自动监视
pred_train = w*x_train + b
loss_train = 0.5*tf.reduce_mean(tf.square(y_train-pred_train)) #计算训练集上的误差
pred_test = w*x_test+b
loss_test = 0.5*tf.reduce_mean(tf.square(y_test-pred_test)) #计算测试集上的误差
mse_train.append(loss_train)
mse_test.append(loss_test)
dL_dw,dL_db = tape.gradient(loss_train,[w,b]) #使用训练集中的数据更新模型参数
w.assign_sub(learn_rate*dL_dw)
b.assign_sub(learn_rate*dL_db)
if i % display_step == 0:
print("i: %i,Train Loss: %f,Test Loss: %f"%(i,loss_train,loss_test)) #输出训练误差和测试误差
plt.figure(figsize=(15,10))
plt.subplot(221)
plt.scatter(x_train,y_train,color = 'b',label = "data") #绘制散点图
plt.plot(x_train,pred_train,color = 'r',label = 'model')#蓝色的点是房间数的散点图,红线是训练得到的线性模型
plt.legend(loc = "upper left")
plt.subplot(222)
plt.plot(mse_train,color = 'b',linewidth=3,label = "train loss")
plt.plot(mse_test,color = 'r',linewidth=1.5,label = 'test loss')
plt.legend(loc = "upper left")#损失值和迭代次数变化的曲线
plt.subplot(223)
plt.plot(y_train,color = 'b',marker= "o",label = "true")
plt.plot(pred_train,color = 'r',marker = '.',label = 'predict')
plt.legend()#训练集实际房价和预测值的比较
plt.subplot(224)
plt.plot(y_test,color = 'b',marker= "o",label = "true")
plt.plot(pred_test,color = 'r',marker = '.',label = 'predict')
plt.legend()#测试集实际房价和预测值的比较
plt.show()
end=time.process_time()
print("程序执行时间:",end-start)

题目二:
使用波士顿房价数据集中的所有属性,训练多元线性回归模型,并测试其性能,以可视化的形式展现训练和测试模型的过程及结果。
要求:
(1)编写代码实现上述功能;
(2)记录超参数的调试过程,寻找使模型达到最佳性能的超参数;
(3)分析和总结:
在题目一和本题中,分别选择单一属性、全部属性建立和训练模型,比较两者的学习率、迭代次数等超参数,以及在训练集和测试集上的交叉熵损失、准确率和模型训练时间,以表格或其他合适的图表形式展示。分析以上结果,可以得到什么结论,或对你有什么启发。
代码:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
boston_housing=tf.keras.datasets.boston_housing
(train_x,train_y), (test_x,test_y) = boston_housing.load_data() #加载数据集
train_X=train_x[:,[5,12]]#数据处理,第6和13个属性,低收入人口及房屋面积
test_X=test_x[:,[5,12]]
num_train=len(train_X)
num_test=len(test_X)
x_train=(train_X-train_X.min(axis=0))/(train_X.max(axis=0)-train_X.min(axis=0))#数据处理
y_train=train_y
x_test=(test_X-test_X.min(axis=0))/(test_X.max(axis=0)-test_X.min(axis=0))
y_test=test_y
x0_train=np.ones(num_train).reshape(-1,1)
x0_test=np.ones(num_test).reshape(-1,1)
X_train=tf.cast(tf.concat([x0_train,x_train],axis=1),tf.float32)
X_test=tf.cast(tf.concat([x0_test,x_test],axis=1),tf.float32)
Y_train=tf.constant(y_train.reshape(-1,1),tf.float32)
Y_test=tf.constant(y_test.reshape(-1,1),tf.float32)
learn_rate=0.01#设置超参数
iter=2000
display_step=200
np.random.seed(612)#设置模型变量初始值
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)
mse_train=[]
mse_test=[]
for i in range(0,iter+1):
with tf.GradientTape() as tape:
PRED_train=tf.matmul(X_train,W)
Loss_train=0.5*tf.reduce_mean(tf.square(Y_train-PRED_train))
PRED_test=tf.matmul(X_test,W)
Loss_test=0.5*tf.reduce_mean(tf.square(Y_test-PRED_test))
mse_train.append(Loss_train)
mse_test.append(Loss_test)
dL_dW=tape.gradient(Loss_train,W)
W.assign_sub(learn_rate*dL_dW)
if i % display_step == 0:
print("i: %i,Train Loss: %f,Test Loss: %f"% (i,Loss_train,Loss_test))
plt.figure(figsize=(20,4))#可视化输出
plt.subplot(131)
plt.ylabel("MSE")
plt.plot(mse_train,color="blue",linewidth=3)
plt.plot(mse_test,color="red",linewidth=1.5)
plt.subplot(132)
plt.plot(y_train,color="blue",marker="o",label="true_price")
plt.plot(PRED_train,color="red",marker=".",label="predict")
plt.legend(loc="upper right")
plt.ylabel("Price")
plt.subplot(133)
plt.plot(y_test,color="blue",marker="o",label="true_price")
plt.plot(PRED_test,color="red",marker=".",label="predict")
plt.legend(loc="upper right")
plt.ylabel("Price")
plt.show()

题目三:
从波士顿房价数据集中选择合适的属性使用多元线性回归模型预测房屋价格。
要求:
(1)属性分析:
观察波士顿房价数据集的可视化结果,分析各个属性对房价的影响。找出你认为最佳的属性组合,并说明理由;
(2)建立和训练模型:
编写代码,建立并训练多元线性回归模型预测房价,并测试模型性能;
(3)记录实验过程和结果:
记录超参数的调试过程,寻找使模型达到最佳性能的超参数、迭代次数和训练时间,并记录训练和测试过程及结果;
(4)分析和总结:
比较分别使用单一属性、全部属性和你自己选择的属性组合训练模型时,学习率、迭代次数等参数,以及在训练集和测试集上的交叉熵损失、准确率和训练时间等结果,以表格或其他合适的图表形式展示。通过以上结果,可以得到什么结论,或对你有什么启发。
代码:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
boston_housing=tf.keras.datasets.boston_housing
(train_x,train_y), (test_x,test_y) = boston_housing.load_data() #加载数据集
train_X=train_x[:,[5,12]]#数据处理,第6和13个属性,低收入人口及房屋面积
test_X=test_x[:,[5,12]]
num_train=len(train_X)
num_test=len(test_X)
x_train=(train_X-train_X.min(axis=0))/(train_X.max(axis=0)-train_X.min(axis=0))#数据处理
y_train=train_y
x_test=(test_X-test_X.min(axis=0))/(test_X.max(axis=0)-test_X.min(axis=0))
y_test=test_y
x0_train=np.ones(num_train).reshape(-1,1)
x0_test=np.ones(num_test).reshape(-1,1)
X_train=tf.cast(tf.concat([x0_train,x_train],axis=1),tf.float32)
X_test=tf.cast(tf.concat([x0_test,x_test],axis=1),tf.float32)
Y_train=tf.constant(y_train.reshape(-1,1),tf.float32)
Y_test=tf.constant(y_test.reshape(-1,1),tf.float32)
learn_rate=0.01#设置超参数
iter=2000
display_step=200
np.random.seed(612)#设置模型变量初始值
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)
mse_train=[]
mse_test=[]
for i in range(0,iter+1):
with tf.GradientTape() as tape:
PRED_train=tf.matmul(X_train,W)
Loss_train=0.5*tf.reduce_mean(tf.square(Y_train-PRED_train))
PRED_test=tf.matmul(X_test,W)
Loss_test=0.5*tf.reduce_mean(tf.square(Y_test-PRED_test))
mse_train.append(Loss_train)
mse_test.append(Loss_test)
dL_dW=tape.gradient(Loss_train,W)
W.assign_sub(learn_rate*dL_dW)
if i % display_step == 0:
print("i: %i,Train Loss: %f,Test Loss: %f"% (i,Loss_train,Loss_test))
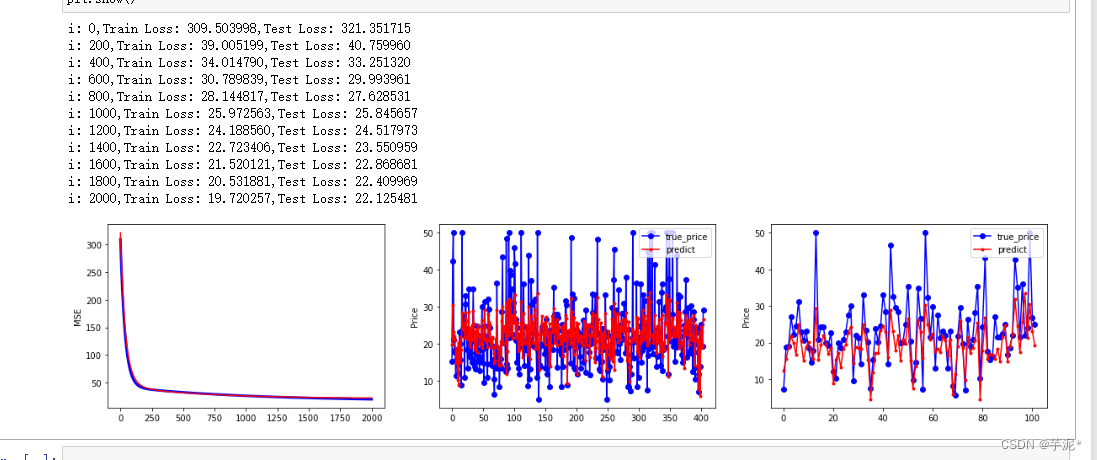
plt.figure(figsize=(20,4))#可视化输出
plt.subplot(131)
plt.ylabel("MSE")
plt.plot(mse_train,color="blue",linewidth=3)
plt.plot(mse_test,color="red",linewidth=1.5)
plt.subplot(132)
plt.plot(y_train,color="blue",marker="o",label="true_price")
plt.plot(PRED_train,color="red",marker=".",label="predict")
plt.legend(loc="upper right")
plt.ylabel("Price")
plt.subplot(133)
plt.plot(y_test,color="blue",marker="o",label="true_price")
plt.plot(PRED_test,color="red",marker=".",label="predict")
plt.legend(loc="upper right")
plt.ylabel("Price")
plt.show()
4.实验小结
① 实验过程中遇到了哪些问题,你是如何解决的?
数组切片取数据,取的不对.反复尝试.
② 在实验过程中,你认为影响模型性能的因素有哪些?
对数据有没有进行归一化处理,超参数的设置.
③ 梯度下降法可以求解凸函数的全局最小值,当函数是非凸函数时,是否可以使用梯度下降法,得到全局最小值,为什么?
不可以,可能陷入局部极小值
④ 在题目基本要求的基础上,你对每个题目做了那些扩展和提升?或者你觉得在编程实现过程中,还有哪些地方可以进行优化?
多尝试几次超参数的设置,尽量使模型最优
![复现永恒之蓝[MS17_010]](https://img-blog.csdnimg.cn/2aabf4266cfd48ec97163506dae89ea5.png)