目录
死锁是什么？
死锁的三种经典情况
1.一个线程，一把锁，连续加锁两次，如果锁是不可重入锁就会死锁。
不可重入锁与可重入锁：
2.两个线程两把锁，t1和t2各自针对于锁A和锁B加锁，再尝试获取对方的锁。
3.多个线程，多把锁（相当于第二种的一般情况）
死锁的四个必要条件
1.互斥使用
2.不可抢占
3.请求和保持
4.循环等待
如何破除死锁
死锁是什么？
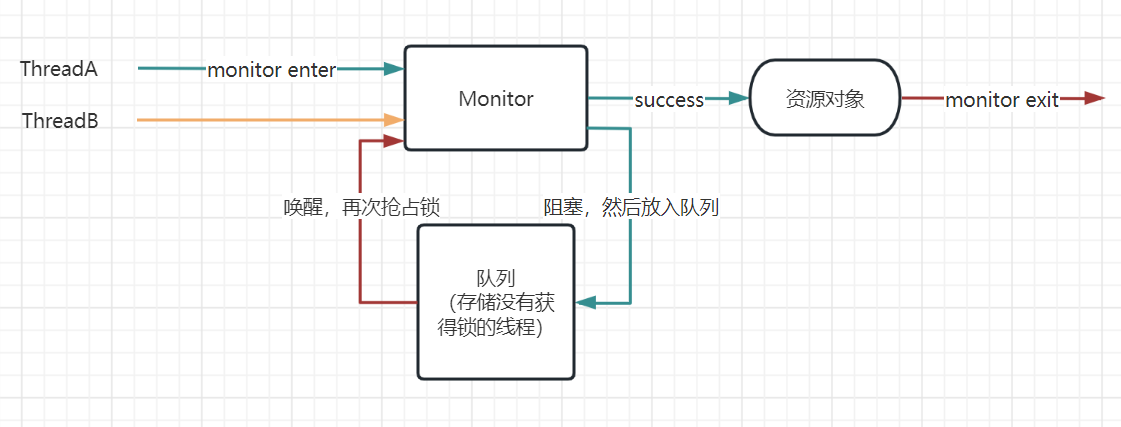
死锁的定义：在并发计算中，死锁是一种 状态，在这种状态下，组中的每个成员等待另一个成员(包括自己)采取行动，例如发送消息或更常见的释放锁。
首先关于死锁，如果存在两个线程：线程1与线程2。
线程1持有锁1，线程2持有锁2。在这种情况下，如果线程1尝试获取锁2，同时线程2尝试获取锁1。那么线程1就要等线程2释放锁2才能获取到锁2，而线程2释放锁2的前提是线程2获取到了锁1。也就是说，线程1在等待线程2释放锁2，而线程2也在等待线程1释放锁1.在这种情况下，线程1与线程2对峙着，陷入死等的情况。也就是我们所说的死锁。
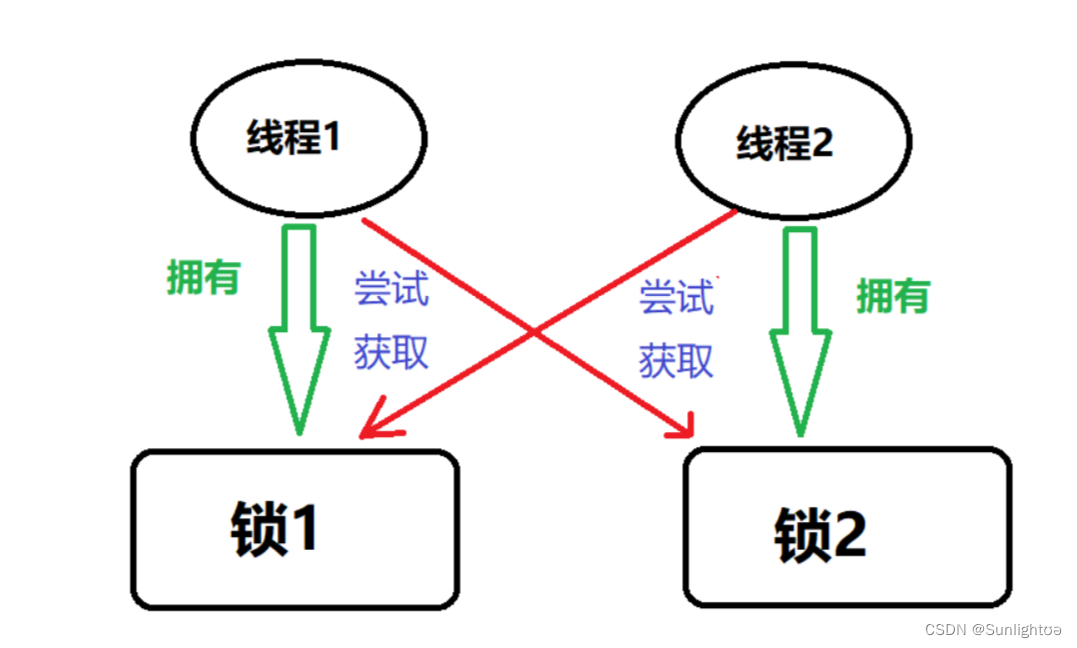
死锁的三种经典情况
1.一个线程，一把锁，连续加锁两次，如果锁是不可重入锁就会死锁。
在这里涉及到一个概念：不可重入锁。那么什么是不可重入锁？什么是可重入锁？（此处仅为简单介绍，后续会单独介绍不可重入锁和可重入锁）
不可重入锁：
一个线程在第一次加锁后没有释放锁，然后又尝试再次的加锁。
但是此时第一个锁没有被释放，那么第二个锁只能阻塞等待，直到第一次加的锁被释放出来。此时会出现死锁问题。
可重入锁：
可重入锁在第一次加锁后再进行第二次加锁不会出现死锁问题。
一个线程针对于同一个对象连续加锁两次，若会存在问题则是不可重入锁。不会存在问题则是可重入锁。
2.两个线程两把锁，t1和t2各自针对于锁A和锁B加锁，再尝试获取对方的锁。
3.多个线程，多把锁（相当于第二种的一般情况）
经典案例：
哲学家就餐问题。
哲学家就餐问题可以这样表述，假设有五位哲学家围坐在一张圆形餐桌旁，做以下两件事情之一：吃饭，或者思考。吃东西的时候，他们就停止思考，思考的时候也停止吃东西。每位哲学家面前都有一份面，每两个哲学家之间有一只餐叉。因为用一只餐叉很难吃到意大利面，所以假设哲学家必须用两只餐叉吃东西。他们只能使用自己左右手边的那两只餐叉。这种情况 可能产生死锁，每个哲学家都拿着左手的餐叉，永远都在等右边的餐叉（或者相反）。即使没有死锁，也有可能发生资源耗尽。
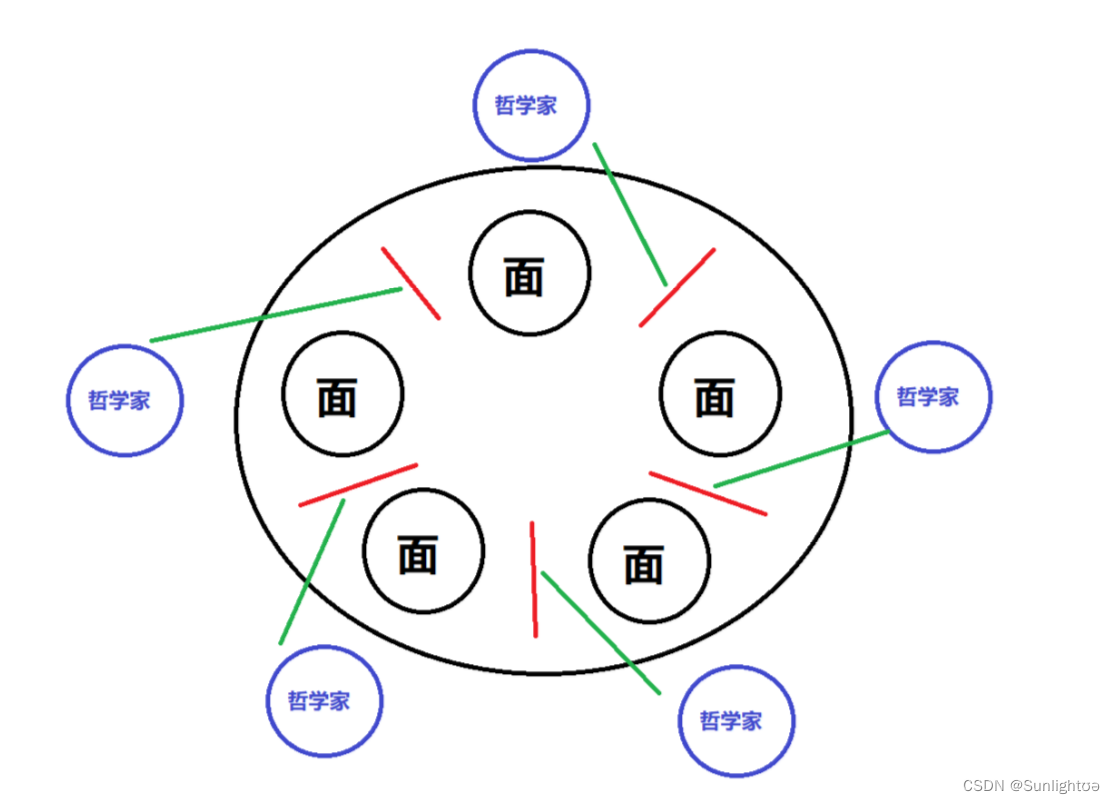
所以这个时候我们就需要想办法来解决这些哲学家们就餐的问题。
我们在这里先讲述一个简单的解法：
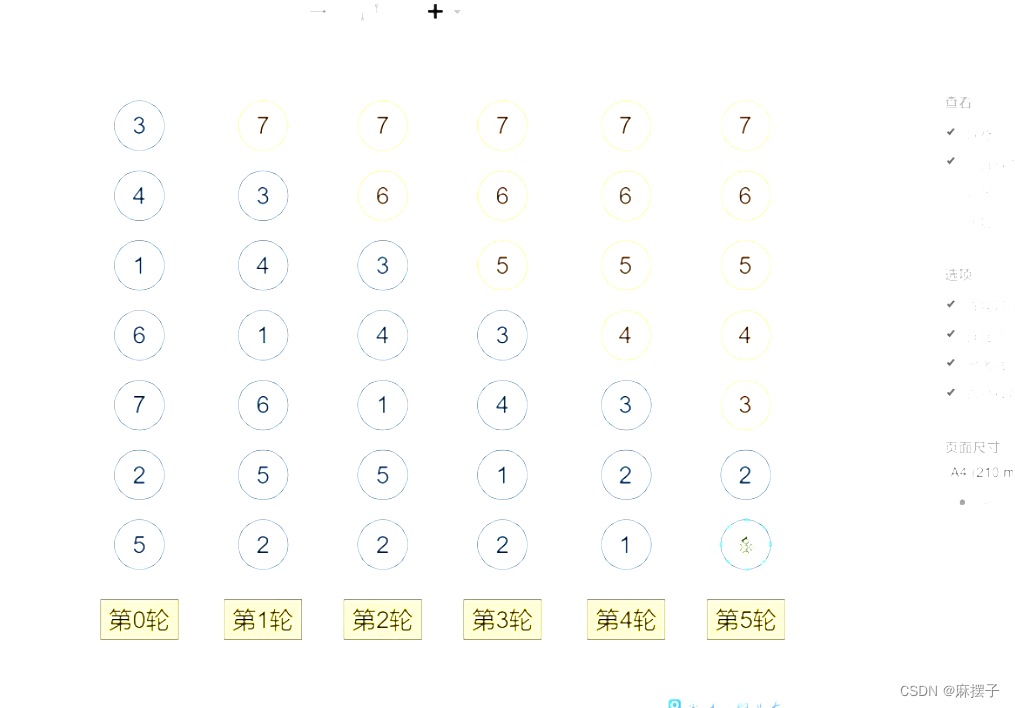
首先我们先为这些哲学家们编上编号，再为这些餐叉编上编号。
先让其中4个哲学家进行用餐，那么一定有一位哲学家拿到两个餐叉，在0号哲学家用完餐后，释放这两个餐叉。接着1号哲学家拿起4，3号餐叉进行用餐，剩余的哲学家都如上述方法进行用餐。
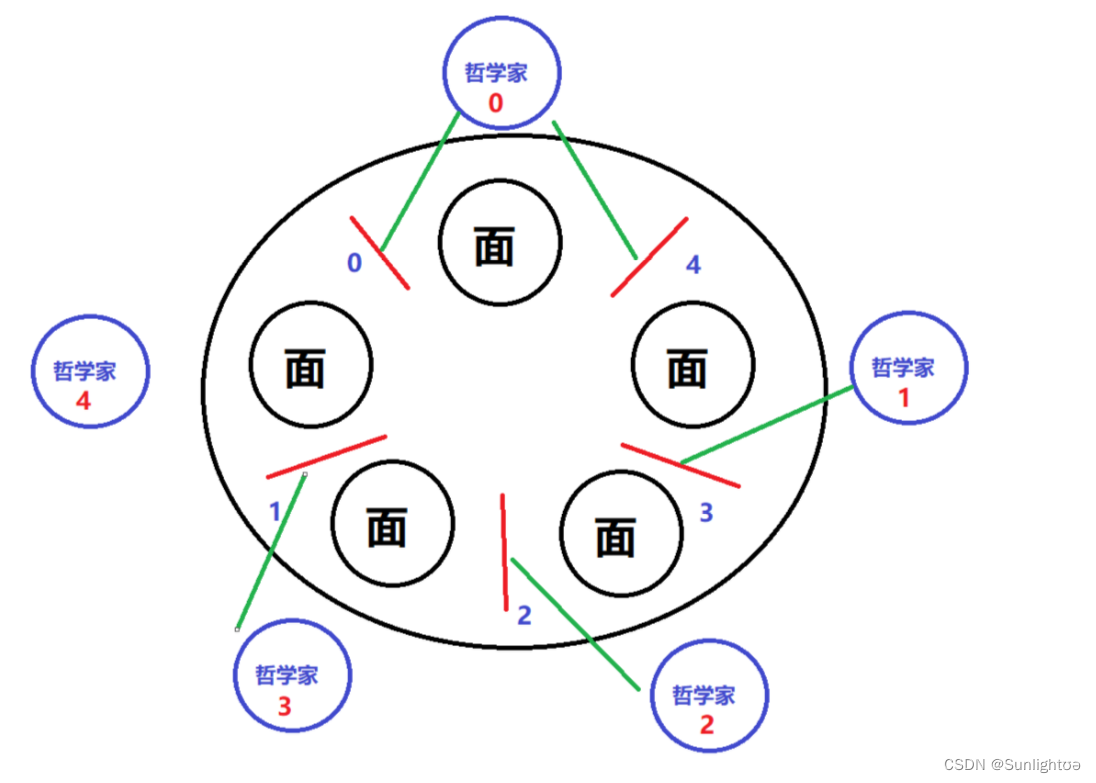如同上图所示。
那么如何保证4号哲学家拿不到他左侧的筷子呐？这个时候需要对其左侧的筷子进行加锁操作。
死锁的四个必要条件
提示一下：这四个必要条件 同时具备才会出现死锁。
1.互斥使用
线程1拿到了锁，线程2就要等着。
2.不可抢占
线程1拿到锁后，必须是由线程1主动释放，不能是线程2强行将锁拿到手。
3.请求和保持
线程1拿到锁A后，再尝试获取锁B，A这把锁还是继续保持着的（就像你谈了女朋友，然后在没有和现任分手的情况下又想和另外一个女孩子在一起）。
4.循环等待
线程1拿到锁A后，尝试再获取到锁B。线程2拿到锁B后，尝试再拿到锁A。然后就变成了线程1等待线程2释放锁B，线程2等待线程1释放锁A。
如何破除死锁
由于死锁的四个必要条件中的前三个条件都是锁的基本特征没办法进行修改，所以我们只能从第4个条件入手进行突破。
那么就是说：
解决死锁最有效的办法就是破除循环等待。
而破除循环等待的办法是： 给锁加个编号，然后指定一个固定的顺序（如从小到大）来进行加锁。任意线程加多把锁的时候，都让线程遵守上述的顺序，此时循环等待就会被破除，死锁问题就会被解决。
