十大算法基础——上（共有20道例题，大多数为简单题）

一、枚举（Enumerate）算法

定义：就是一个个举例出来，然后看看符不符合条件。
举例：一个数组中的数互不相同，求其中和为0的数对的个数。

for (int i = 0; i < n; ++i)
  for (int j = 0; j < i; ++j)
    if (a[i] + a[j] == 0) ++ans;

例题1：204. 计数质数

题目难度：中等

方法1：枚举（会超时）
考虑到如果 y 是 x 的因数，那么 $\dfrac{x}{y}$ 也必然是 x 的因数，因此我们只要校验 y 或者 $\dfrac{x}{y}$ 即可。而如果我们每次选择校验两者中的较小数，则不难发现较小数一定落在 $[2,\sqrt{x}]$ 的区间中，因此我们只需要枚举 $[2,\sqrt{x}]$ 中的所有数即可。

class Solution {
public:
    bool isPrime(int x) //判断x是否是质数
    {
        for (int i = 2; i * i <= x; ++i) 
        {
            if (x % i == 0) 
            {
                return false;//不是质数
            }
        }
        return true;//是质数
    }

    int countPrimes(int n) {
        int ans = 0;
        for (int i = 2; i < n; ++i) {
            ans += isPrime(i);
        }
        return ans;
    }
};

方法2：埃氏筛
如果 x 是质数，那么大于 x 的倍数 2x,3x,…一定不是质数，因此我们可以从这里入手。

class Solution 
{
public:
    int countPrimes(int n) 
    {
        vector<int> isPrime(n, 1);//一开始全标记为1
        int ans = 0;
        for (int i=2; i<n; ++i) 
        {
            if (isPrime[i]) 
            {
                ans += 1;//2，3必是质数               
                for (int j=2*i; j<n; j+=i) 
                {
                    isPrime[j]=0;
                    //i是质数，i的倍数(j)肯定不是质数，赋值为0
                }                
            }
        }
        return ans;
    }
};

例题2：等差素数列

题目难度：简单

#include <iostream>
using namespace std;

//判断n是否是素数
int check(int n)
{
  for(int i=2;i<n;i++)
  {
    if(n%i==0) return 0;//不是素数
  }
  return 1;//是质数
}

int main()
{
  int len=0;
  int gc;//公差
  int num;//序列的第一个数
  int ans=0;

  for(num=2;num<=1000;num++)
  {
    if(check(num))//检查第一个数字是不是素数
    {
      for(gc=1;gc<=1000;gc++)//从1开始枚举公差
      {
        for(int j=1;j<1000;j++)
        {
          if(check(num+j*gc)) ans++;//代表是素数
          else 
          {
            ans=0;
            break;//推出当前for循环
          }
          if(ans==9) //从0开始计数，ans=0时就已经有一个
          {
            cout<<gc;
            return 0;
          }
        }
      }
    }
  }
  return 0;
}

例题3：1925. 统计平方和三元组的数目

题目难度：简单

class Solution {
public:
    int countTriples(int n) 
    {
        int ans=0;
        for(int a=1;a<=n;a++)
        {
            for(int b=a+1;b<+n;b++)
            {
                for(int c=b+1;c<=n;c++)
                {
                    if(a*a+b*b==c*c) ans+=1;                   
                }
            }
        }
        return ans*2;
    }
};

例题4：2367. 算术三元组的数目

题目难度：简单

方法1：暴力

class Solution {
public:
    int arithmeticTriplets(vector<int>& nums, int diff) 
    {
        int size=nums.size();
        int num=0;//算术三元组的数目

        for(int i=0;i<size;i++)
        {
            for(int j=i+1;j>i&&j<size;j++)
            {
                if(nums[j]-nums[i]==diff)
                {
                    for(int k=j+1;k>j&&k<size;k++)
                    {
                        if(nums[k]-nums[j]==diff) 
                        {
                            num=num+1;
                            break;//退出当前for（k）循环
                        }
                        else continue;
                    }
                } 
                else continue;           
            }
        }
        return num;    
    }
};

方法2：哈希表，用哈希表记录每个元素，然后遍历 nums，看 nums[j]−diff 和 nums[j]+diff 是否都在哈希表中。

class Solution {
public:
    int arithmeticTriplets(vector<int>& nums, int diff) {
        int n = nums.size();
        unordered_set<int> st;
        for (int x : nums) st.insert(x);//将nums数组里的值插入到哈希表st中    
            
        int ans = 0;
        for (int i = 0; i < n; i++) 
        {
            if (st.count(nums[i] +diff) > 0 && st.count(nums[i] + 2*diff) > 0) 
            {
                ans++;
            }
        }
        return ans;
    }
};

例题5：2427. 公因子的数目（会）

题目难度：简单

class Solution {
public:
    int commonFactors(int a, int b) 
    {
        int min_data=min(a,b);//找a,b之间的最小值
        int num;
        for(int i=1;i<=min_data;i++)//公因数一定小于a和b的最小值
        {
            if(a%i==0&&b%i==0)//公因子的定义
            {
                ++num;
            }
        }
        return num;        
    }
};

例题6：2240. 买钢笔和铅笔的方案数（会）

题目难度：中等

class Solution {
public:
    long long waysToBuyPensPencils(int total, int cost1, int cost2) 
    {
        int total1=total/cost1;//最多买几支钢笔
        int total2=total/cost2;//最多买几支铅笔
        long long num=0;
        for(int i=0;i<=total1;i++)
        {                
            if(total-i*cost1>=0)//买完钢笔后还能买几只铅笔
            {
                int new_total=total-i*cost1;
                num+=new_total/cost2; 
                num=num+1; 
            }        
        }
        return num;
    }
};

例题7：2310. 个位数字为 K 的整数之和（不会）

题目难度：中等

class Solution {
public:
    int minimumNumbers(int num, int k) 
    {
        if(num==0) return 0;//当 num=0时，唯一的方法是选择一个空集合，答案为0
        for(int i=1;i<=10;i++)//num>0时，我们可以发现最多不会选择超过10个数。
        //这是因为如果这些数的个位数字为 k，并且我们选择了至少 11个数，由于11*k(10*k+k)的个位数字也为k，那么我们可以把任意的11个数合并成1个，使得选择的数仍然满足要求，并且集合更小。
        {
            if(i*k<=num&&(num-i*k)%10==0) return i;
            //i*k<=num:由于每个数最小为 k，那么这 i 个数的和至少为 i⋅k。如果i⋅k>num，那么无法满足要求。
            //这 i 个数的和的个位数字已经确定，即为 i*k mod 10。
            //我们需要保证其与 num 的个位数字相同，这样 num−i⋅k 就是 10 的倍数，我们把多出的部分加在任意一个数字上，都不会改变它的个位数字。
        } 
        return -1;      
    }
};

二、模拟算法

定义：模拟就是用计算机来模拟题目中要求的操作。

例题8：爬动的蠕虫

题目难度：简单

#include <iostream>
using namespace std;
#include <algorithm>

int main()
{
    int n,u,d;
    cin>>n>>u>>d;
    int x=0;//爬的高度
    int num=0;//爬的分钟数
    while (true) 
    {  // 用死循环来枚举
        x += u;
        num++;//爬一分钟
        if (x>= n) break;  // 满足条件则退出死循环
        num++;//休息一分钟
        x -= d;
    }
    cout<<num;
    return 0;
}

例题9：1920. 基于排列构建数组

题目难度：简单

class Solution {
public:
    vector<int> buildArray(vector<int>& nums) 
    {
        int size=nums.size();
        vector<int> ans(size,0);

        for(int i=0;i<size;i++)
        {
            ans[i]=nums[nums[i]];
        }
        return ans;
    }
};

例题10：方程整数解

题目难度：简单

#include <iostream>
using namespace std;
int main()
{
  // 请在此输入您的代码
  for(int i=1;i<1000;i++)
  {
    for(int j=i;j<1000;j++)
    {
      for(int k=j;k<1000;k++)
      {
        if(i*i+j*j+k*k==1000&&i!=6&&j!=8&&k!=30)
        {
          cout<<min(min(i,j),k);
          return 0;
        }
      }
    }
  }
  return 0;
}

例题11：等差数列

题目难度：简单

#include <iostream>
using namespace std;
#include <algorithm>
#include <vector>
int main()
{
    // 请在此输入您的代码
    int n;
    cin >> n;
    vector<int> arr(n);
    int diff;
    int ans = n;
    for (int i = 0; i < n; i++)
    {
        cin >> arr[i];
    }
    sort(arr.begin(), arr.end());
    //cout << "从小到大排序后：";
    //for (int i = 0; i < n; i++)
    //{
        //cout << arr[i] <<" ";
    //}
    //cout << endl;
    vector<int> diff_vector(n-1);
    int min_value;
    for (int j = 0; j < n -1; j++)
    {
        diff_vector[j] = arr[j + 1] - arr[j];
    }
    min_value = *min_element(diff_vector.begin(), diff_vector.end());
    //cout << min_value << endl;;

    for (int k = 0; k < n - 1; k++)
    {
        if (arr[k + 1] - arr[k] != min_value)
        {
            diff = arr[k + 1] - arr[k];
            ans += (diff / min_value)-1;
        }
    }
    if (arr[1] == arr[0]) cout << n;
    else cout << ans;
    return 0;
}

例题12：方格填数（不会）

题目难度：简单

#include <iostream>
#include<algorithm>
using namespace std;
int main()
{
  // 请在此输入您的代码
  int ans=0;//填数方案
  int num[]={0,1,2,3,4,5,6,7,8,9};
  
  do{
      if(abs(num[0]-num[1])!=1&&abs(num[0]-num[3])!=1
      &&abs(num[0]-num[4])!=1&&abs(num[0]-num[5])!=1
      &&abs(num[1]-num[4])!=1&&abs(num[1]-num[2])!=1
      &&abs(num[1]-num[5])!=1&&abs(num[1]-num[6])!=1
      &&abs(num[2]-num[5])!=1&&abs(num[2]-num[6])!=1
      &&abs(num[3]-num[4])!=1&&abs(num[3]-num[7])!=1&&abs(num[3]-num[8])!=1
      &&abs(num[4]-num[5])!=1&&abs(num[4]-num[7])!=1
      &&abs(num[4]-num[8])!=1&&abs(num[4]-num[9])!=1
      &&abs(num[5]-num[8])!=1&&abs(num[5]-num[9])!=1&&abs(num[5]-num[6])!=1
      &&abs(num[6]-num[9])!=1&&abs(num[7]-num[8])!=1&&abs(num[8]-num[9])!=1){ans++;}
    }while(next_permutation(num,num+10));
    cout<<ans<<endl;

  return 0;
}

next_permutation 全排列函数
需要引用的头文件：

#include <algorithm>

函数原型：

bool std::next_permutation<int *>(int *_First, int *_Last)

（1）基本格式：

int a[];
do{
//循环体
}while(next_permutation(a,a+n));//表达式
//全排列生成好了next_permutation函数返回0，会跳出while循环。

（2）举例：

#include <algorithm>
#include <string>
#include <iostream>
#using namespace std;
int main()
{
    string s = "aba";
    sort(s.begin(), s.end());//排序aab
    do {
        cout << s << '\n';//先执行一次这行，再去执行while的表达式
    } while(next_permutation(s.begin(), s.end()));
    //do…while 是先执行一次循环体，然后再判别表达式。
    //当表达式为“真”时，返回重新执行循环体，如此反复，直到表达式为“假”为止，此时循环结束。
}
//输出：aab 
//aba
//baa

#include<iostream>
#include<algorithm>
using namespace std;
int main() 
{
	int a[4] = { 0 }, n;
	cin >> n;
	for (int i = 0; i <n; i++)
	{
		cin >> a[i];
	}
	do{
		for (int i = 0; i <n; ++i)
		{
			cout << a[i] << " ";
		}
		cout << endl;
	} while (next_permutation(a, a + n));
	return 0;
}
//输入：4
//2 5 1 3
//输出：
//2 5 1 3
//2 5 3 1
//3 1 2 5
//3 1 5 2
//3 2 1 5
//3 2 5 1
//3 5 1 2
//3 5 2 1
//5 1 2 3
//5 1 3 2
//5 2 1 3
//5 2 3 1
//5 3 1 2
//5 3 2 1

三、递归(Recursion)算法

递归代码最重要的两个特征：结束条件和自我调用。自我调用是在解决子问题，而结束条件定义了最简子问题的答案。
递归的缺点：在程序执行中，递归是利用堆栈来实现的。每当进入一个函数调用，栈就会增加一层栈帧，每次函数返回，栈就会减少一层栈帧。而栈不是无限大的，当递归层数过多时，就会造成栈溢出的后果。
如何优化递归：深度优先搜索（DFS）/记忆化搜索（动态规划的一种）

例题13：剑指 Offer 64. 求1+2+…+n

题目难度：中等
使用递归会出现的问题：终止条件需要使用 if ，因此本方法不可取。
思考：除了 if还有什么方法？答：逻辑运算符

a&&b
如果a是false，那么就不会继续执行b
a||b
如果a是true，就不会继续执行b

class Solution {
public:
    int num=0;
    int sum=0;//总和
    int sumNums(int n) 
    {
        //递归
        num=n;
        sum+=num;
        --num;
        num>=1&&sumNums(num);//也可换成num==0||sumNums(num);
        return sum;
    }
};

例题14：231. 2 的幂

题目难度：简单

class Solution {
public:
    bool isPowerOfTwo(int n) 
    {
        if(n==1) return true;//终止条件
        if(n<=0) return false;
        bool res=false;
        if(n%2==0)
        {
            n=n/2;
            res=isPowerOfTwo(n);
        }
        return res;
    }
};

例题15：509. 斐波那契数

题目难度：简单

class Solution {
public:
    int fib(int n) 
    {
    	//截至条件
        if(n==0) return 0;
        if(n==1) return 1;
        //递推关系
        return fib(n-1)+fib(n-2);
    }
};

四、分治（Divide and Conquer）算法

定义：就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。
过程
分治算法的核心思想就是分而治之。大概的流程可以分为三步：分解-> 解决-> 合并。

分解原问题为结构相同的子问题。
分解到某个容易求解的边界之后，进行递归求解。
将子问题的解合并成原问题的解。

分治法能解决的问题一般有如下特征：

该问题的规模缩小到一定的程度就可以容易地解决。
该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质，利用该问题分解出的子问题的解可以合并为该问题的解。
该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题

区别
（1）递归与枚举的区别
递归和枚举的区别在于：枚举是横向地把问题划分，然后依次求解子问题；而递归是把问题逐级分解，是纵向的拆分。
（2）递归与分治的区别
递归是一种编程技巧，一种解决问题的思维方式；分治算法很大程度上是基于递归的，解决更具体问题的算法思想。

例题16：53. 最大子数组和（不会）

题目难度：中等

class Solution {
public:
    struct Status 
    {
        int lSum, rSum, mSum, iSum;
    };
    Status pushUp(Status l, Status r) 
    {
        //lSum 表示[l,r] 内以 l 为左端点的最大子段和
        //rSum 表示 [l,r] 内以 r 为右端点的最大子段和
        //mSum 表示 [l,r] 内的最大子段和
        //iSum 表示 [l,r] 的区间和

        //首先最好维护的是iSum，区间 [l,r] 的iSum 就等于左子区间的 iSum 加上右子区间的 iSum
        int iSum = l.iSum + r.iSum;
       
        //对于[l,r]的lSum。存在两种可能，它要么等于左子区间的 lSum，
        //要么等于左子区间的 iSum加上右子区间的 lSum。二者取大。
        int lSum = max(l.lSum, l.iSum + r.lSum);

        //对于[l,r]的 rSum，同理，它要么等于右子区间的 rSum，
        //要么等于右子区间的 iSum 加上左子区间的 rSum，二者取大。
        int rSum = max(r.rSum, r.iSum + l.rSum);

        //当计算好上面的三个量之后，就很好计算[l,r]的mSum了。
        //我们可以考虑[l,r]的mSum对应的区间是否跨越 m。
        //它可能不跨越 m，也就是说 [l,r]的 mSum 可能是左子区间的 mSum 和右子区间的 mSum 中的一个
        //它也可能跨越 m，可能是左子区间的 rSum 和 右子区间的 lSum 求和。三者取大。
        int mSum = max(max(l.mSum, r.mSum), l.rSum + r.lSum);
        return (Status) {lSum, rSum, mSum, iSum};
    }

    Status get(vector<int> &a, int l, int r) 
    {
        if (l == r) 
        {
            return (Status) {a[l], a[l], a[l], a[l]};
        }
        int m = (l + r) >> 1;
        Status lSub = get(a, l, m);
        Status rSub = get(a, m + 1, r);
        return pushUp(lSub, rSub);
    }
    int maxSubArray(vector<int>& nums) 
    {
        return get(nums, 0, nums.size() - 1).mSum;
    }

};

五、十大排序算法

术语：
（1）稳定排序：如果 a 原本在 b 的前面，且 a=b，排序之后 a 仍然在 b 的前面，则为稳定排序。
（2）非稳定排序：如果 a 原本在 b 的前面，且 a=b，排序之后 a 可能不在 b 的前面，则为非稳定排序。
（3）原地排序：原地排序就是指在排序过程中不申请多余的存储空间，只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
（4）非原地排序：需要利用额外的数组来辅助排序。

（一）选择排序

定义：首先，找到数组中最小的那个元素，其次，将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。其次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。这种方法我们称之为选择排序。
性质：(1)时间复杂度： $O(n^2)$ (2)空间复杂度： $O (1)$ (3)非稳定排序 (4)原地排序
优点：不占用额外的内存空间。缺点：时间复杂度高

//从小到大排序
template<typename T> 
void selection_sort(vector<T>& arr) 
{
	for (int i = 0; i < arr.size()-1; i++) 
    {
    	int min = i;
        for (int j = i + 1; j < arr.size(); j++)
        {
        	if (arr[j] < arr[min])
            {
            	min = j;//记录最小值
            }
        }
       swap(arr[i], arr[min]);//交换i与min对应的值
    }
}

例题17：2418. 按身高排序

题目难度：简单

class Solution {
public:
    vector<string> sortPeople(vector<string>& names, vector<int>& heights) 
    {
        for (int i = 0; i < heights.size()-1; i++) 
        {
    	    int max = i;
            for (int j = i + 1; j < heights.size(); j++)
            {
        	    if (heights[j] > heights[max])
                {
            	    max = j;//记录最大值
                }
            }
            swap(heights[i],heights[max]);//交换i与max对应的值
            swap(names[i], names[max]);
        }
        return names;  
    }
};

（二）插入排序

定义:插入排序（Insertion sort）是一种简单直观的排序算法。它的工作原理为将待排列元素划分为已排序和未排序两部分，每次从未排序的元素中选择一个插入到已排序的元素中的正确位置。从数组第2个(从i=1开始)元素开始抽取元素key，把它与左边第一个(从j=i-1开始)元素比较，如果左边第一个元素比它大，则继续与左边第二个元素比较下去，直到遇到不比key大的元素(arr[j] <= key)，然后插到这个元素的右边(arr[j+1] = key)。继续选取第3，4，…n个元素。
如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。
性质：(1)时间复杂度： $O(n^2)$ (2)空间复杂度： $O (1)$ (3)稳定排序 (4)原地排序

//从小到大排序
void insertion_sort(int a[], int n)
{
    for(int i= 1; i<n; i++)
    {  
        int j= i-1;
        int key = a[i];
        while(j>=0 && a[j]>key)
        //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
        {  
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = key;//插入到正确位置    
    }
}

例题18：977. 有序数组的平方

题目难度：简单

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) 
    {
    	//耗时太长
        //先平方整个数组
        for(int i=0;i<nums.size();i++)
        {
            nums[i]=nums[i]*nums[i];
        }
        //插入排序     
        for(int i=1;i<nums.size();i++)
        {
            int key=nums[i];
            int j=i-1;
            while(j>=0&&key<nums[j])//当key>=nums[]时，把key插到num[i]的右边
            {
                nums[j+1]=nums[j];
                j--;
            }
            nums[j+1]=key;//这里j+1是因为上面j--
        }
        return nums;
    }
};

（三）希尔排序

定义：希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位；
希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。
性质：(1)时间复杂度： $O (n l o g n)$ (2)空间复杂度： $O (1)$ (3)非稳定排序 (4)原地排序

void shell_sort(vector<int>& arr,int n)
{
	int key;
	int j;
	//初始增量inc为n/2
	for(int inc=n/2;inc>0;inc/=2)//假设inc=12/2，6/2=3，3/2=1；
	{
		//每一趟采用插入排序
		for(int i=inc;i<n;i++)//搞清楚这里为什么是i++，因为是从inc开始一直到n-1，让inc和0，inc+1和1，inc+2和2……n-1与n-1-inc两两相比较
		{
			key=arr[i];
			for(j=i;j>=inc&&arr[j-inc]>key;j-=inc)
			{
				arr[j]=arr[j-inc];
			}
			arr[j]=key;
		}
	}
}

例题19：912. 排序数组

题目难度：中等

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) 
    {
        int n=nums.size();
        int key;
        int j;
	//初始增量inc为n/2
	    for(int inc=n/2;inc>0;inc/=2)//假设inc=12/2，6/2=3，3/2=1；
	    {
		//每一趟采用插入排序
		    for(int i=inc;i<n;i++)//搞清楚这里为什么是i++，因为是从inc开始一直到n-1，让inc和0，inc+1和1，inc+2和2……n-1与n-1-inc两两相比较
		    {
			    key=nums[i];
			    for(j=i;j>=inc&&nums[j-inc]>key;j-=inc)
			    {
				    nums[j]=nums[j-inc];
			    }
			    nums[j]=key;
		    }
	    }
        return nums;
    }
};

（四）冒泡排序

定义：冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。
从小到大排序的步骤：
（1）比较相邻的元素。如果第一个比第二个大，就交换他们两个。
（2）对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
（3）针对所有的元素重复以上的步骤，除了数列末尾已经排序好的元素。持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
性质：1、时间复杂度： $O(n^2)$ 2、空间复杂度： $O (1)$ 3、稳定排序 4、原地排序

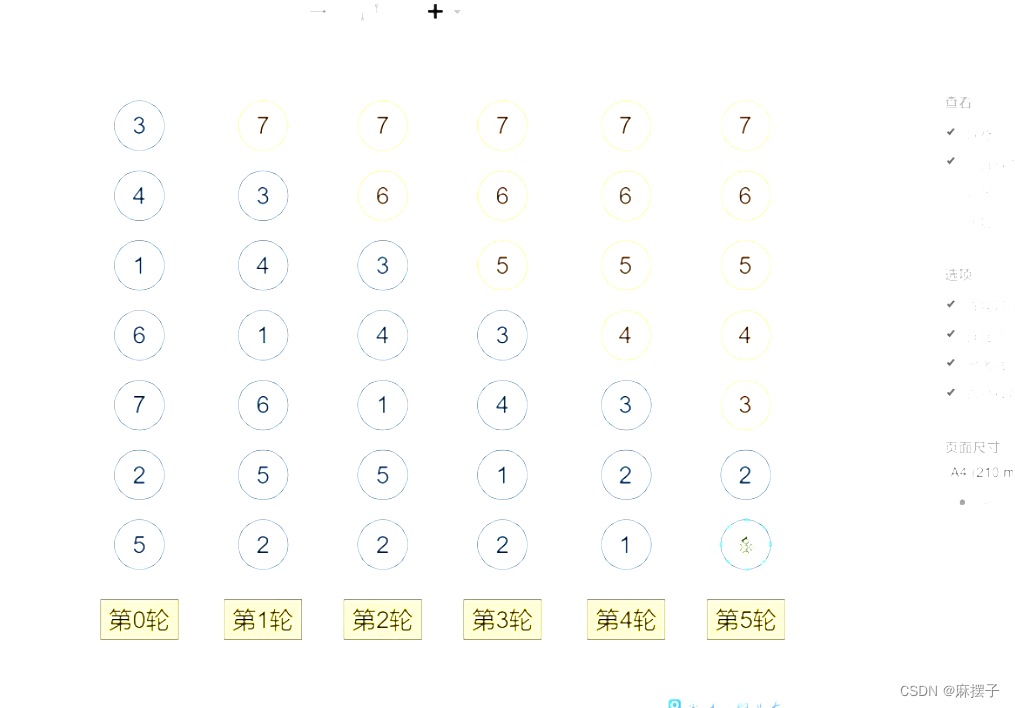
#include <iostream>
using namespace std;
template<typename T> //整数或浮点数皆可使用,若要使用类(class)或结构体(struct)时必须重载大于(>)运算符
//从小到大排序
void bubble_sort(T arr[], int len) //len是arr的长度
{
    int i, j;
    for (i = 0; i < len - 1; i++)//轮数
    {
        for (j = 0; j < len - 1 - i; j++)//每一轮要交换几次
        {
        	if (arr[j] > arr[j + 1])
        	{
        		swap(arr[j], arr[j + 1]);
        	}
         }
	}
}
int main() {
        int arr[] = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
        int len = (int) sizeof(arr) / sizeof(*arr);
        bubble_sort(arr, len);
        for (int i = 0; i < len; i++)
                cout << arr[i] << ' ';
        cout << endl;
        float arrf[] = { 17.5, 19.1, 0.6, 1.9, 10.5, 12.4, 3.8, 19.7, 1.5, 25.4, 28.6, 4.4, 23.8, 5.4 };
        len = (float) sizeof(arrf) / sizeof(*arrf);
        bubble_sort(arrf, len);
        for (int i = 0; i < len; i++)
                cout << arrf[i] << ' '<<endl;
        return 0;
}

（五）计数排序

定义：计数排序（Counting sort）是一种线性时间的排序算法。它的工作原理是使用一个额外的计数数组 C，其中数组C中第 i 个元素是待排序数组 A 中值等于 i 的元素的个数，然后根据数组 C 来将 A 中的元素排到正确的位置。计数排序是一种适合于最大值和最小值的差值不是不是很大的排序。
算法的步骤如下：
（1）找出待排序的数组中最大和最小的元素，那么计数数组C的长度为最大值减去最小值+1。
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项。
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）。
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。
性质：(1)时间复杂度： $O (n + k)$ (2)空间复杂度： $O (k)$ (3)稳定排序 (4)非原地排序

//a是待排序数组，b是排序后的数组，cnt是额外数组
//从小到大排序
void counting_sort() 
{
	if(a.size()<2) return;
	//寻找最大元素
	//int max=a[0];
	//for(int i=0;i<a.size();i++)
	//{
		//if(a[i]>max) max=a[i];
	//}
	int max = *max_element(heights.begin(), heights.end());
	// void *memset(void *str, int c, size_t n) ：复制字符 c（一个无符号字符）到参数 str 所指向的字符串的前 n 个字符。
	//分配一个长度为（max-min+1）的计数数组来存储计数
   // memset(cnt, 0, sizeof(int)*(max-min+1));//cnt变成全0数组，清零
    vector<int> count(max+1,0);//下标为0，1，2，……，max
	//计数
    for (auto x:a) ++cnt[x];//统计数组中每个值为x的元素出现的次数，存入数组cnt的第x项
    
    for (int i = 1; i <= w; ++i) cnt[i] += cnt[i - 1];//统计出现次数，w是cnt的长度
    
    for (int i=0;i<len;i++

) 
    {
    	b[cnt[a[i]]-1] = a[i];
    	--cnt[a[i]];
    }//反向填充目标数组，n是数组a的长度
}

例题20：1051. 高度检查器

题目难度：简单
注意到本题中学生的高度小于等于100，因此可以使用计数排序。

class Solution {
public:
    int heightChecker(vector<int>& heights) 
    {
        int len=heights.size();
        int num=0;
        
        //寻找最大元素
	    // int max=a[0];
	    // for(int i=0;i<a.size();i++)
	    // {
		//     if(a[i]>max) max=a[i];
	    // }
        int max = *max_element(a.begin(), a.end());
        //计数数组初识化为0
        vector<int> count(max+1,0);//下标为0，1，2，……，max
        //计数
        for(int i=0;i<len;i++)
        {
            count[heights[i]]++;
        }
        //统计计数的累计值
        for(int i=1;i<max+1;i++)
        {
            count[i]+=count[i-1];
        }
        //创建输出数组expected
        vector<int> expected(len);
        for(int i=0;i<len;i++)
        {
            expected[count[heights[i]]-1]=heights[i];//count[heights[i]]-1是元素正确的位置
            count[heights[i]]--;
        }
        //找不同的下标数量
        for(int i=0;i<len;i++)
        {
            if(heights[i]!=expected[i]) num++;
        }
        return num;
    }
};