代码随想录算法训练营第十六天 | 104.二叉树的最大深度、559.n叉树的最大深度，111.二叉树的最小深度，222.完全二叉树的节点个数

Day15 周日休息

一、参考资料

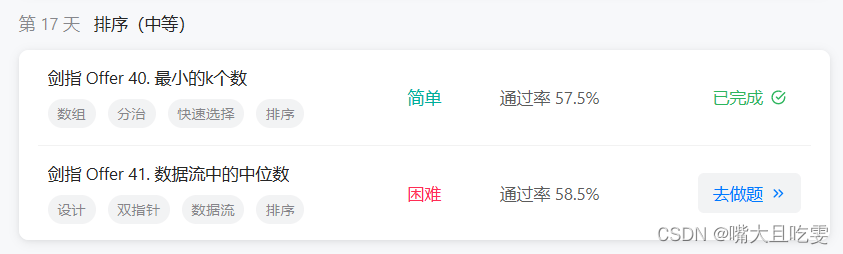
二叉树的最大深度（优先掌握递归）

题目链接/文章讲解/视频讲解： https://programmercarl.com/0104.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%9C%80%E5%A4%A7%E6%B7%B1%E5%BA%A6.html

二叉树的最小深度（优先掌握递归）

题目链接/文章讲解/视频讲解：https://programmercarl.com/0111.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%9C%80%E5%B0%8F%E6%B7%B1%E5%BA%A6.html

完全二叉树的节点个数（优先掌握递归）

题目链接/文章讲解/视频讲解：https://programmercarl.com/0222.%E5%AE%8C%E5%85%A8%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E8%8A%82%E7%82%B9%E4%B8%AA%E6%95%B0.html

二、LeetCode104.二叉树的最大深度

https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
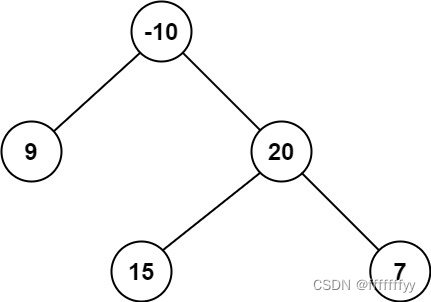
给定二叉树 [3,9,20,null,null,15,7]，
3 / \ 9 20 / \ 15 7
返回它的最大深度 3 。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
// version1：递归法 —— 根节点的高度就是二叉树的最大深度
    int getdepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftdepth = getdepth(node->left);   // 左
        int rightdepth = getdepth(node->right); // 右
        int depth = max(leftdepth, rightdepth) + 1;
        return depth;
    }
    int maxDepth(TreeNode* root) {
        return getdepth(root);
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
// version2：递归法 —— 根节点的高度就是二叉树的最大深度(简化版)
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
// version1和version2采用的均为后序遍历（左右中），当然也可以通过前序遍历（中左右）实现
// version3：递归法 —— 前序遍历，充分表现深度回溯的过程
    int result;
    void getdepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result;  // 中
        if (node->left == NULL && node->right == NULL) return;
        // 左
        if (node->left) {
            depth++;    // 深度+1
            getdepth(node->left, depth);
            depth--;    // 回溯，深度-1
        }
        // 右
        if (node->right) {
            depth++;
            getdepth(node->right, depth);
            depth--;
        }
        return ;
    }

    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        getdepth(root, 1);
        return result;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
// version4：递归法 —— 前序遍历，充分表现深度回溯的过程(简化代码)
    int result;
    void getdepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result;  // 中
        if (node->left == NULL && node->right == NULL) return;
        // 左
        if (node->left) {
            getdepth(node->left, depth + 1);
        }
        // 右
        if (node->right) {
            getdepth(node->right, depth + 1);
        }
        return ;
    }

    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        getdepth(root, 1);
        return result;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // version5: 迭代法
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int depth = 0;
        if (root == NULL) return 0;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return depth;
    }
};

三、LeetCode559.n叉树的最大深度

https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/description/

示例1：

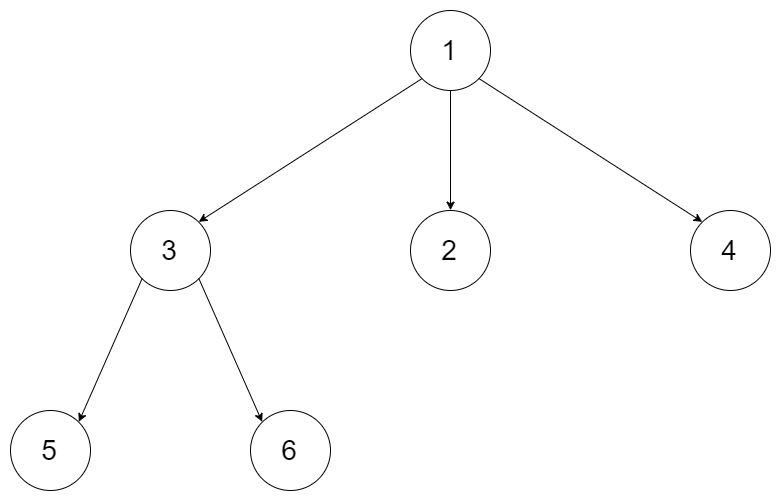
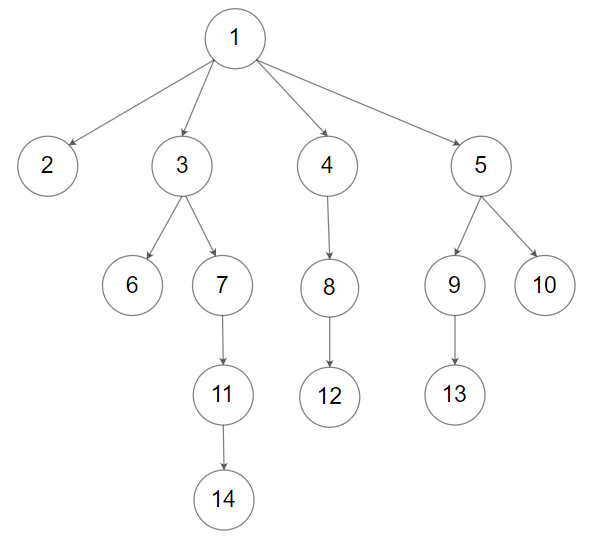
示例2：

给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：（如上图）
输入：root = [1,null,3,2,4,null,5,6] 输出：3
示例 2：（如上图）
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：5
提示:
树的深度不会超过 1000 。
树的节点数目位于 [0, 104] 之间。

// 递归法
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        if (root == NULL) return 0;
        int depth = 0;
        for (int i = 0; i < root->children.size(); i++) {
            depth = max (depth, maxDepth(root->children[i]));
        }
        return depth + 1;
    }
};

// 迭代法
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        queue<Node*> que;
        if (root != NULL) que.push(root);
        int depth = 0;
        while (!que.empty()) {
            int size = que.size();
            depth++;
            for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                for (int j = 0; j < node->children.size(); j++) {
                    if (node->children[j]) que.push(node->children[j]);
                }
            }
        }
        return depth;        
    }
};

四、LeetCode111.二叉树的最小深度

https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/

示例1：

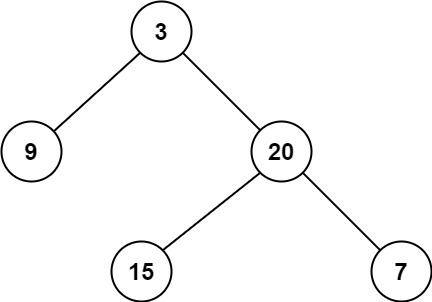
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

示例 1：（如上图）
输入：root = [3,9,20,null,null,15,7] 输出：2
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6] 输出：5

提示：
树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

// 递归法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getDepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftDepth = getDepth(node->left);
        int rightDepth = getDepth(node->right);

        // 当一个左子树为空，右不为空，这时并不是最低点
        if (node->left == NULL && node->right != NULL) {
            return 1 + rightDepth;
        }

        // 当一个左子树不为空，右为空，这时并不是最低点
        if (node->left != NULL && node->right == NULL) {
            return 1 + leftDepth;
        }
        
        int result = 1 + min(leftDepth, rightDepth);
        return result;
    }

    int minDepth(TreeNode* root) {
        return getDepth(root);
    }
};

// 简化版递归法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right != NULL) {
            return 1 + minDepth(root->right);
        }
        if (root->left != NULL && root->right == NULL) {
            return 1 + minDepth(root->left);
        }
        return 1 + min(minDepth(root->left), minDepth(root->right));
    }
};

// 迭代法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        int depth = 0;
        queue<TreeNode*> que;
        if (root == NULL) return 0;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
                if (!node->left && !node->right){
                    return depth;
                }
            }
        }
        return depth;
    }
};

五、LeetCode222.完全二叉树的节点个数

https://leetcode.cn/problems/count-complete-tree-nodes/description/

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。
完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：
输入：root = [1,2,3,4,5,6] 输出：6
示例 2：
输入：root = [] 输出：0
示例 3：
输入：root = [1] 输出：1
提示：
树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是完全二叉树

// 递归法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getNodesSum(TreeNode* cur) {
        if (cur == NULL) return 0;
        int leftNum = getNodesSum(cur->left);
        int rightNum = getNodesSum(cur->right);
        int treeNum = leftNum + rightNum + 1;
        return treeNum;
    }
    int countNodes(TreeNode* root) {
        return getNodesSum(root);
    }
};

// 简化版递归法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == NULL) return 0;
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

// 迭代法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        int result = 0;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                result++;
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return result;
    }
};

总结：

递归的三要素在写之前需要先想明白，另外，由于先完成“层序遍历”的缘故，反而对于迭代法的写法更加熟练，还要多回顾哈！

刷题加油鸭~~