©PaperWeekly 原创 · 作者 | 周正阳
单位 | 中国科学技术大学

论文简介
动态时空图数据结构在多种不同的学科中均普遍存在,如交通流、空气质量观测、社交网络等,这些观测往往会随着时间而变化,进而引发节点间关联的动态时变特性。本文的主要研究对象是动态时空图的回归任务,赋能交通、空气质量和气候预测。动态图学习中聚合偏离目标信息的邻居会导致图学习性能下降,因而我们重新审视了节点的邻居关系,通过对邻居关联进行分类并筛选有助于预测的有效信息进行聚合。
在本文中,我们借助图学习中的“同配性理论(homophily theory)”,提出了动态图“目标同配性度量方法”和“逐层重要性量化策略”,将同配性理论从静态图拓展至具有时空特性的动态图中。其中,目标同配理论捕获了目标状态与当前状态的差异性,通过构建有向符号以动态地、针对性地选择与目标一致的同配节点,即有效邻居实现节点级聚合;层重要性量化利用局部拓扑环境和目标感知度量不同传播层的有效信息量,以实现逐层有效传播。
本文在 ICLR 2023 评审过程中得分为 8,8,6,6,被接收为 Poster。

论文标题:
GReTo: Remedying Dynamic Graph Topology-Task Discordance via Target Homophily
论文地址:
https://openreview.net/pdf?id=8duT3mi_5n

研究动机
拓扑-任务不一致性:现有的动态图回归任务往往使用图卷积神经网络(GCN),以物理连接或特征相似度构建邻接矩阵来进行节点级聚合。
如图 1 所示,以交通流量为例,节点 A 从 T 至 T+1 时间步发生了明显的流量增加,而此时在 T 步聚合大于其本身的节点 C/D/G 将是有效获得目标的策略,反之聚合其他节点则可能导致与任务目标相悖的结果,因而不是所有的(预定义)物理的拓扑均为有效,而当节点 A 在时序层面变化较大,则可能在 T 步直接聚合同配邻居也将失效。
因此,鉴于动态时空图具有节点关系多样性、动态性和时序演进关系,直接利用同配邻居或某一固定的拓扑结构进行消息传递会不可避免地导致某些时间步的聚合偏离回归目标,我们将这种现象称为拓扑-任务的不一致。因而在时空动态图中拓扑-任务不一致问题是推动动态图预测更精准的必经之路,同时将开拓动态图理论分析、动态图拓扑优化的新方法与新思路。
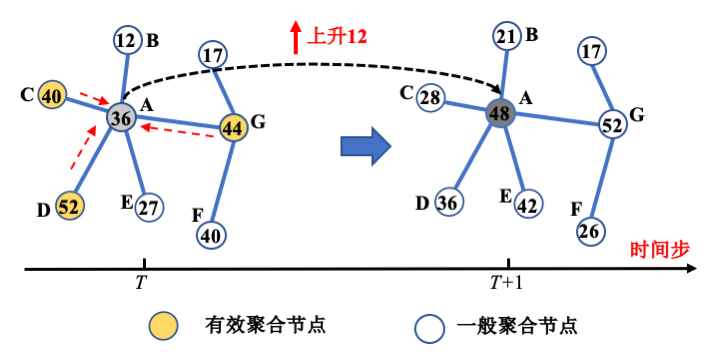
▲ 图1 拓扑-任务不一致性示意图
这一问题的本质原因在于时空图所具有的本质时空异质性,这种异质性体现在不同的时间步、不同区域所具有的节点观测不尽相同,进而带来不同时间步的空间关联和时序依赖关系的不一致性。
在图学习理论中,同配性度量刻画了节点间的关系,其中,若有边相连的一对邻居节点具有相似观测或相同标签,那么这对邻居是一组同配成分,反之,若有边相连的一组邻居具有不同观测或不同的标签,那么其为一组异配成分,而时空动态图上往往同时存在同配和异配成分。
这种关联识别与解耦恰恰为我们的有效节点选择带来了潜在可能。然而,传统的同配性理论大多在静态图和分类任务中开展研究,很少在跨时间步、具有连续观测的动态图回归任务上进行研究,因此,我们认为基于同配理论实现个性化聚合仍然存在以下几个挑战:
1. 如何基于连续值确定节点间的同配关系,并将这种刻画节点关联的范式拓展至连续数据观测?
2. 如何利用不同节点在时序方面的演进趋势和当前节点间的关联,筛选有利于达成预测目标的有效邻居?
3. 如何量化局部邻域信息与目标信息的关联,实现时空异质环境下的图信号高阶传播?
为解决以上挑战,我们重新审视了节点关系,利用同配关系的定义拓展了具有符号和距离的动态图上节点关系度量机制。我们发现,在预测任务中,将同配聚合提升为有符号的目标引导的消息传递,可以有效地解决上述提出的拓扑-任务不一致问题,提高聚合能力。
因此,本文提出了一种新的图神经网络 GReTo,该模型通过构建目标同配性度量来选择有效邻居,进而修正时空数据预测中的拓扑-任务不一致。贡献总结如下:
1. 我们提出了时空图中因异质性带来的拓扑-任务的不一致问题,形式化了动态图同配理论,将同配性理论从静态图分类任务拓展至动态图回归任务,利用图学习理论进一步拓展了时空数据性质分析和时空学习建模方法;
2. 我们提出了一个基于目标同配性修正拓扑结构的图神经网络并建模时空异质性,其包括基于目标同配的有符号信息传递和基于层重要性的高阶图信号传播;
3. 我们在交通、气候、空气质量等不同领域的四个动态图上评估了我们的解决方案,并成功地在 MAPE 指标上实现了 3.20% 到 24.79% 的提升,并表明负异配性越高,有符号的有向消息传递机制将不同成分解耦并聚合的优势越明显。

方法
我们首先构建了动态图的同配性计算机制,该机制由图内空间同配性与图间转移同配性组成。我们的 GReTo 模型将由三个部分构成:1)目标为中心的信息传递;2)个性化高阶逐层传播和 3)时序卷积模块。
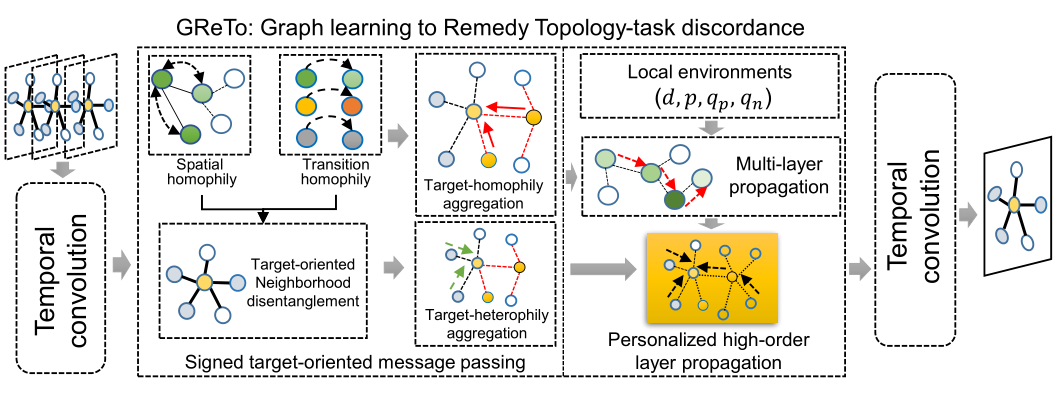
▲ 图2 GReTo模型总览
3.1 同配性度量与邻域同配关系描述向量
定义1:图内空间同配性与图间转移同配性。为适应连续型数值变量的关系度量,我们提出基于符号和阈值的划分方法。具体而言,基于特征距离的分类阈值 ,将图内同配性和图间同配性可以分为三类,正向异配(+1,比给定观测大);同配(,与原有观测相仿);负向异配(-1,比给定观测小)。
对于节点 和 ,同配度量的符号表示 相对于 的方向,即节点 聚合 时, 的节点数值会如何变化,而距离表示相差的程度。给定一个序列图 、时间步长 和节点 ,图内同配性 和图间同配性 分别表示为:
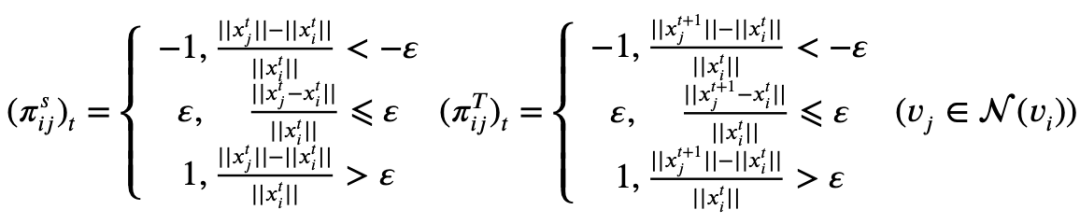
▲ 图3 动态图同配性度量计算机制
其示意图如下:
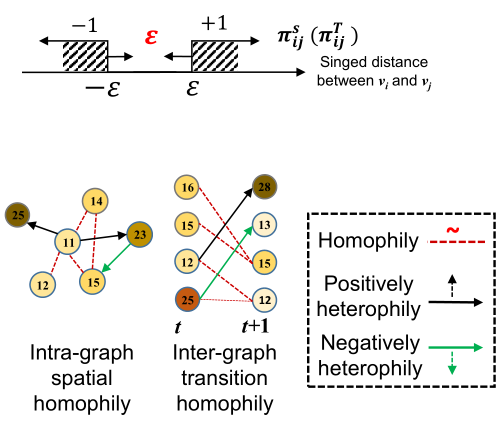
▲ 图4 动态图同配性度量示意
其中,图内同配度量主要承担了同一时间步上的空间上关系度量,而图间同配性搭建起不同时间步图上不同节点间依赖关系的桥梁,用于捕获时序上的演进关系。
定义2:局部邻域环境(LNE)。为利用同配性度量进一步刻画邻域状态,同时描述邻域拓扑和邻居亲和度关系,我们提出了 LNE 度量,即依照正向异配、同配和负向异配三类划分邻域成分,并构成邻域描述向量 :
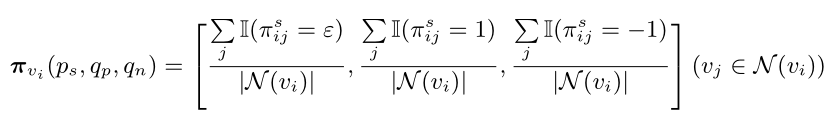
▲ 图5 动态图邻域度量
3.2 目标为中心的消息传递
研究发现,在时空回归预测任务中,当待预测时间步中的观测与当前时间步的观测相差较大时,其无法通过仅聚合当前时间步中的同配邻居回归得到。事实上,图上观测间的关系不仅是现有工作所认为的“同配性”,而是可能同时具有正向关联和负向关联的,如处于上下游的两个路口必然存在正向关联,而处于相同OD中的不同路径中的节点必然存在竞争关系,即你弱我强的负向关联。
因此,将同配邻居的聚合拓展至“有符号的有向聚合”,以不同学习参数聚合正向和负向信息,将提升图表征能力和聚合回归效果。
目标为中心的邻居发现:在时序同配性和空间同配性度量中,若两者符号方向一致,则表示时序演进方向与空间聚合方向一致。基于此,我们将空间同配和时序演进同配耦合,基于图内同配(即当前空间关联)和图间同配(即时序演进方向)度量导出当前时间步的邻域聚合方向。首先,我们构建了 mask 矩阵 ,其由图间同配性与图内同配性相除计算得到:
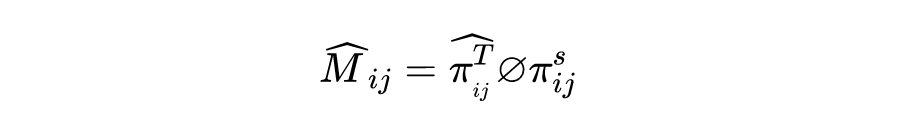
其中 表示按位相除。
以上“相除”的设计使得 中的每个 均为较丰富的边描述,即每个边值不仅可以区分目标为中心的节点(有利于聚合达成目标的节点),还能够度量节点间的接近程度,其中较大的边值意味着更大目标一致性和聚合贡献。通过基于边号对 M 进行分割,我们可以实现面向目标的同配邻居和异配邻居:
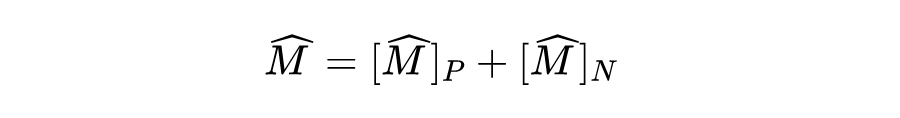
其中, 选中了邻居中与目标演进方向一致的节点,而 选中了与目标演进方向相悖的节点。因此需对这两类节点实行不同的卷积核进行学习。
跨图(图间)转移同配性预测器:鉴于在动态图预测任务中,图间同配性在测试阶段是不获得的,因此我们设计了一个序列分类任务来预测每个节点的图间同配性。分类器的输入是每个节点的前序观测,输出是局部邻域环境向量LNE。我们将取最大的概率值视作为预测得到的 。
解耦的有向信息传递:基于获得的 和 ,可根据不同类型的关联构建有向信息传递。我们将 和 分别施加于邻接矩阵 以获得带符号的邻接矩阵:
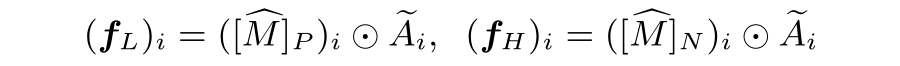
▲ 图6 生成新邻接阵
而后进行聚合:
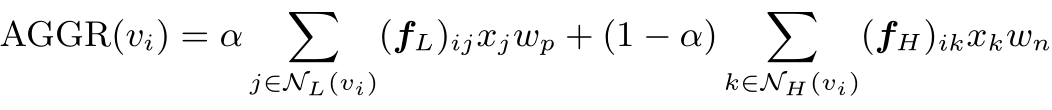
▲ 图7 生成新邻接阵
事实上,在滤波器当中,与给定节点变化方向相一致的邻居可以视作低通信息,而变化方向相异的可以视高通信息,因此,在此处 和 可以分别视作低通和高通滤波器。
个性化的高阶逐层传播:由于 GNN 的层数,即节点的传播深度是一个离散变量,很难对其直接优化,因此,我们设计了一种自适应层重要性度量,利用邻域信息与目标信息间的相似性来量化每一层重要性。我们首先导出了局部环境与传播步数的关系,而后基于该关系提出层重要性度量,并实现图上信号的高阶传播。
局部邻域环境与传播步数的关系:1)给定节点,他的传播步数由每一层的目标同配比率 和该节点 的度有关;2) 和 越小,传播的步数应越大。
自适应层重要性度量:为了获得目标同配的高阶邻居,我们将层重要性量化这一挑战转化为度量高阶邻居分布与跨图时序同配性分布间的一致性。首先,我们可以通过对邻接矩阵进行幂计算获得 在第 k 个传播步的表征 ,而对于跨图时序同配性分布可以由时间序列分类器得到 ,因此 明确包含有目标信息。
因而,我们将 与 进行点积,并保留每一行的最大值以抑制其他非目标同配成分的干扰。该点积获得信息即表示该节点在该层所包含的目标相关的信息量,进一步地,经验表明,度数越大、层数越小,传播深度应越深,因此逐层重要性度量由下式给出:
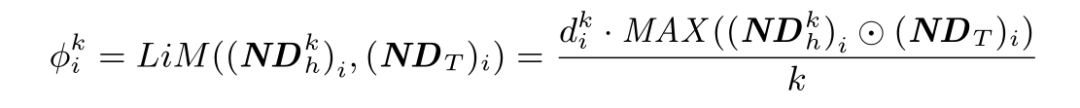
▲ 图8 层重要性
其中 表示节点 在第 层的度。
个性化高阶传播模块
为了获得归一化的逐层传播权值,我们对获得的 施加了可学习的 MLP 变换和 Softmax 函数:
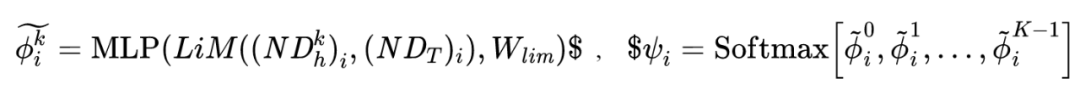
而后,我们即可对其在低通和高通部分分别进行传播,由于高通部分的重要性相较于低通部分较小,我们仅考虑了 引导下的高阶传播:
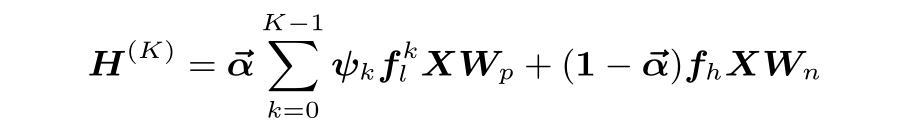
由于动态时空图预测存在多步到单步或多步到多步的情形,我们将该高阶传播模块嵌入到每一时间步中。
时序感知模块
我们沿用了 STGCN 中的三明治结构,将时序学习模块部署于修正的空间依赖学习模块前后,并基于 TCN 实现了时序依赖的捕获:
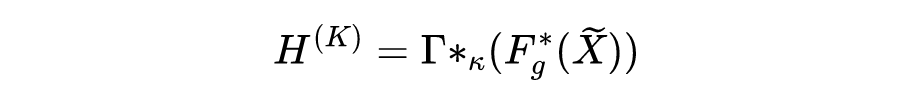
优化目标
最后,我们的优化目标由两方面组成,一是跨图转移同配性预测器,其为一个三分类的序列分类器,二是普通的回归预测任务。因此,我们的优化目标如下:
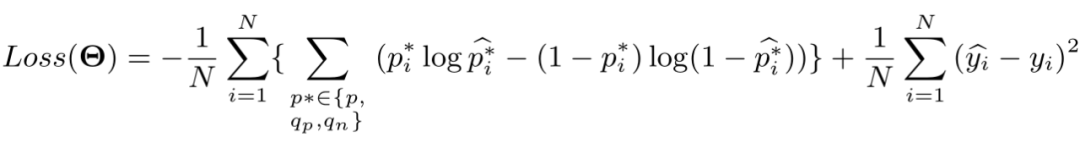

实验
我们在交通流(Metr-LA, PeMS-Bay)空气质量(KnowAir)、气候环境(Temperature)等多个领域的时空动态图数据集上开展了实验。
由于时序跨图同配预测对接下来的任务至关重要,我们首先验证了该预测器的性能,预测准确率如下:
Metr-LA:0.78 PeMS-Bay: 0.60 KnowAir: 0.86 Temperature: 0.68。以上预测的准确率均高于 60%,表明了其可为接下来的邻居同配节点选择提供较好的保障。
实验结果如下图所示。
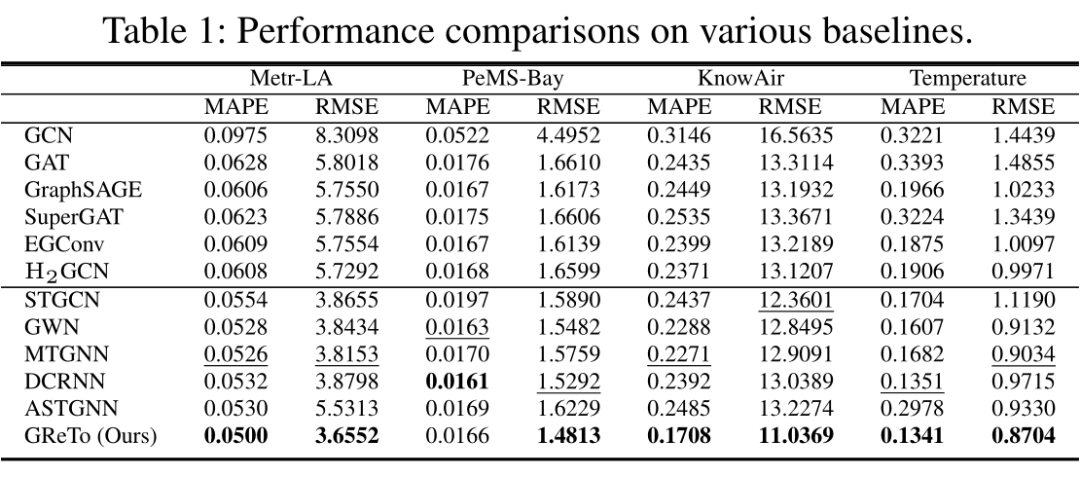
▲ 图11 实验结果
在预测任务中,我们的方法可以获得 3.61%~24.79% 的性能提升。我们发现,具有同配-异配建模能力的 GCN,如 EGConv 和 H2GCN,比不具备异配邻居建模能力的模型预测效果好;同时,我们的方法在异配性较高,尤其是节点负向异配性较高的数据集上性能提升较大,如 KnowAir(负向异配性 = 27%)。
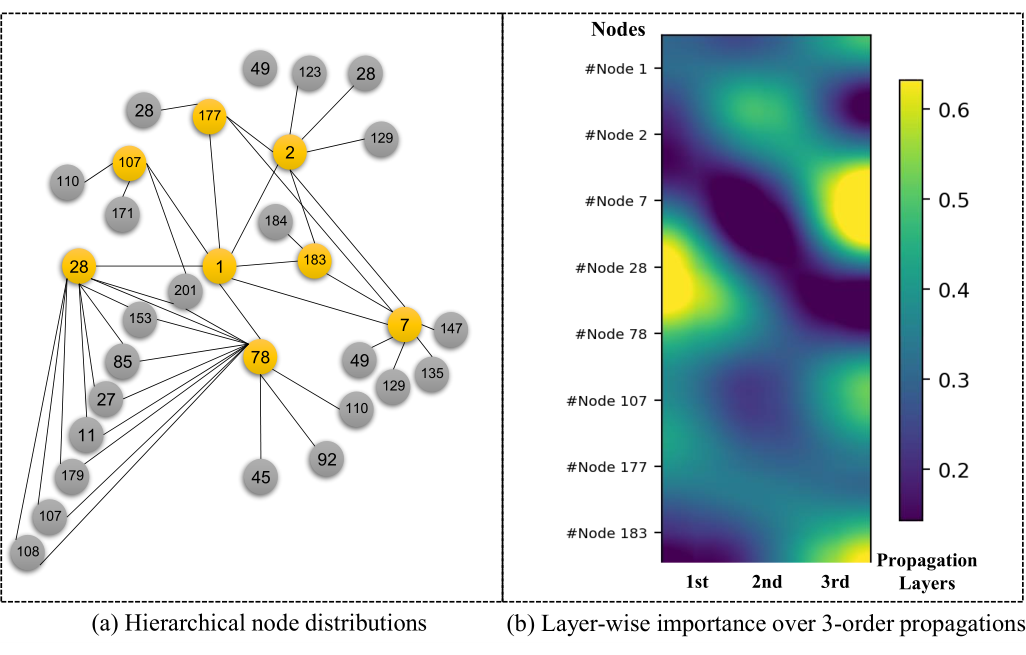
▲ 图12 案例分析
我们将在 Metr-LA 上的数据和模型可视化于下图,其中图(a)表示的是层次性的节点分布(橙色节点表示具有较高 degree 的节点),图(b)展示了 GReTo 在 3 阶 GNN 传播中的权值。我们发现度越小的节点,往往传播层数的越深,而度越高的节点传播层数越小。该案例分析可以为本工作的解释性提供一定支撑。
▲ 图13 案例分析
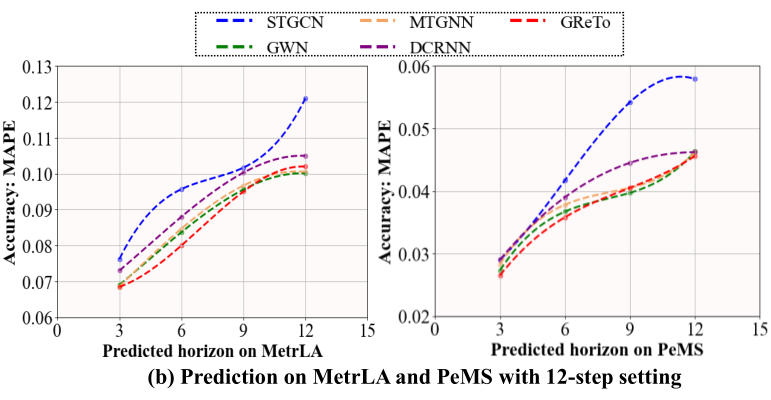
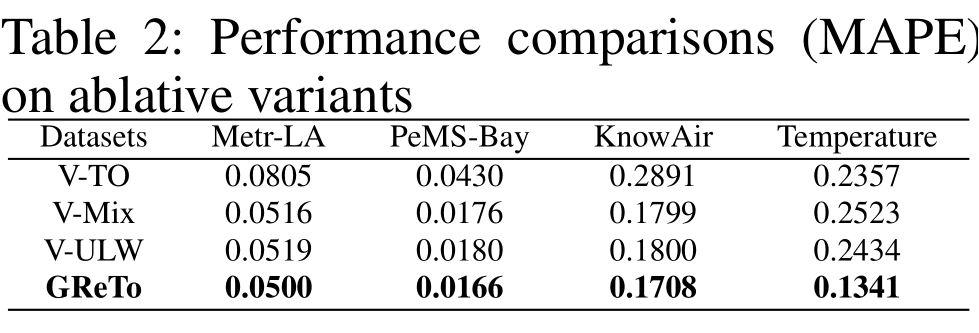
进一步地,消融实验与多步预测实验进一步验证了 GReTo 各模块的有效性与可扩展性。

结论
在本文中,我们从时-空视角重新审视节点关系,提出了动态同配性理论,该同配性理论为动态图数据分析提供了重要手段,同时基于图同配分析,我们展示了拓展多类型邻居聚合可以获得表征能力的提升。
因此,我们提出了一种新的 GNN,GReTo,该 GNN 集成了目标为中心的消息传递和基于层重要性的高阶传播,实验验证了 GReTo 在四种动态图上的优越性。未来,我们将继续研究如何基于同配性理论进一步改进更多类型的动态图学习,例如边类型预测、多步时空图序列预测等。
更多技术细节和实验分析请参见论文原文!同时欢迎从事 GNN、时空学习相关研究的小伙伴一同交流探讨!
更多阅读




#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿

△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
·


![【C#】[带格式的字符串] 复合格式设置字符串与使用 $ 的字符串内插 | 如何格式化输出字符串](https://img-blog.csdnimg.cn/176899f47ce848d38989dff6fee5a0bb.png)