给你一个 m x n 大小的矩阵 grid ，由若干正整数组成。

执行下述操作，直到 grid 变为空矩阵：

从每一行删除值最大的元素。如果存在多个这样的值，删除其中任何一个。
将删除元素中的最大值与答案相加。
注意 每执行一次操作，矩阵中列的数据就会减 1 。

返回执行上述操作后的答案。

示例 1：

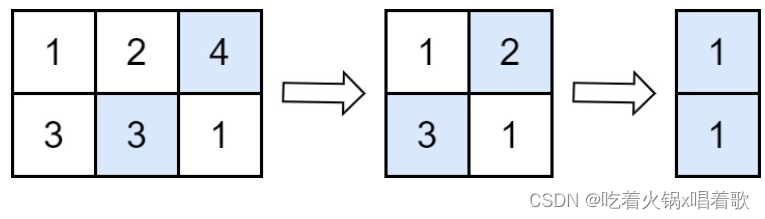
输入：grid = [[1,2,4],[3,3,1]]
输出：8
解释：上图展示在每一步中需要移除的值。

• 在第一步操作中，从第一行删除 4 ，从第二行删除 3（注意，有两个单元格中的值为 3 ，我们可以删除任一）。在答案上加 4 。
• 在第二步操作中，从第一行删除 2 ，从第二行删除 3 。在答案上加 3 。
• 在第三步操作中，从第一行删除 1 ，从第二行删除 1 。在答案上加 1 。
  最终，答案 = 4 + 3 + 1 = 8 。

把每行排序，然后对每一列的最大值求和：

class Solution {
public:
    int deleteGreatestValue(vector<vector<int>>& grid) {
        for (vector<int> &row : grid) {
            sort(row.begin(), row.end());
        }

        int ret = 0;
        while (!grid[0].empty()) {
            int colMax = 0;
            for (vector<int> &row : grid) {
                if (colMax < row.back()) {
                    colMax = row.back();
                }
                row.pop_back();
            }
            ret += colMax;
        }
        
        return ret;
    }
};