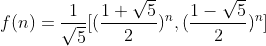文章标题
- LeetCode 20. 有效的括号
- 题目链接🔗
- 思路
- 代码实现
- LeetCode 1047. 删除字符串中的所有相邻重复项
- 题目链接🔗
- 思路
- 代码实现
- LeetCode 150. 逆波兰表达式求值
- 题目链接🔗
- 思路
- 代码实现
LeetCode 20. 有效的括号
题目链接🔗
LeetCode 20. 有效的括号
思路
先来分析一下 这里有三种不匹配的情况
-
第一种情况,字符串里左方向的括号多余了 ,所以不匹配

-
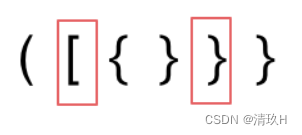
第二种情况,括号没有多余,但是 括号的类型没有匹配上
-
第三种情况,字符串里右方向的括号多余了,所以不匹配
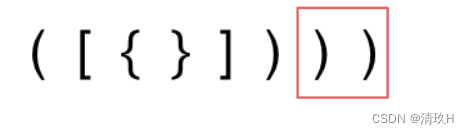
我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性
动画如下:

代码实现
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
char ch;
for (int i = 0; i < s.length() ;i++){
ch = s.charAt(i);
if (ch == '('){
stack.push(')');
}else if (ch == '{'){
stack.push('}');
}else if (ch == '['){
stack.push(']');
}else if (stack.isEmpty() || stack.peek() != ch){
return false;
}else {
stack.pop();
}
}
return stack.isEmpty();
}
LeetCode 1047. 删除字符串中的所有相邻重复项
题目链接🔗
LeetCode 1047. 删除字符串中的所有相邻重复项
思路
我们在删除相邻重复项的时候,其实就是要知道当前遍历的这个元素,我们在前一位是不是遍历过一样数值的元素,那么如何记录前面遍历过的元素呢?
所以就是用栈来存放,那么栈的目的,就是存放遍历过的元素,当遍历当前的这个元素的时候,去栈里看一下我们是不是遍历过相同数值的相邻元素。
然后再去做对应的消除操作。 如动画所示:

从栈中弹出剩余元素,此时是字符串ac,因为从栈里弹出的元素是倒序的,所以再对字符串进行反转一下,就得到了最终的结果。
代码实现
public String removeDuplicates(String s) {
Stack<Character> stack = new Stack<>();
char ch;
for (int i = 0; i < s.length(); i++) {
ch = s.charAt(i);
if (stack.isEmpty() || ch != stack.peek()){
stack.push(ch);
}else {
stack.pop();
}
}
String str = "";
//剩余的元素即为不重复的元素
while (!stack.isEmpty()) {
str = stack.pop() + str;
}
return str;
}
LeetCode 150. 逆波兰表达式求值
题目链接🔗
LeetCode 150. 逆波兰表达式求值
思路
其实逆波兰表达式相当于是二叉树中的后序遍历。 我们可以把运算符作为中间节点,按照后序遍历的规则画出一个二叉树。
但我们没有必要从二叉树的角度去解决这个问题,只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了,就可以了。

代码实现
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList();
for (String s : tokens) {
if ("+".equals(s)) { // leetcode 内置jdk的问题,不能使用==判断字符串是否相等
stack.push(stack.pop() + stack.pop()); // 注意 - 和/ 需要特殊处理
} else if ("-".equals(s)) {
stack.push(-stack.pop() + stack.pop());
} else if ("*".equals(s)) {
stack.push(stack.pop() * stack.pop());
} else if ("/".equals(s)) {
int temp1 = stack.pop();
int temp2 = stack.pop();
stack.push(temp2 / temp1);
} else {
stack.push(Integer.valueOf(s));
}
}
return stack.pop();
}