一,题目

Description

给出一棵树N个点及数字K

接下来N-1行描述有关边的开始点，结束点.

保证图中不会有环

接下来K个数字，代表你要走过的点的编号.当然你可以自己选择出发点及行进的路线

不一定按给定编号顺序前行,求走过的最短距离。

Format

Input

第一行给出N,K。

2 <= N<= 50000,1<=K<=N

接下来N-1行，描述这个树

最后一行给出K个数字，代表点的编号。1<=编号<=N

Output

如题

Samples

输入数据 1

4 2

1 2

4 2

2 3

1 3

输出数据 1

2

输入数据 2

11 3

1 2

1 3

3 4

4 5

5 11

3 6

6 7

7 8

8 9

9 10

2 10 11

输出数据 2

12

Hint

注意当K=1的情况

---

二,思路

这道题其实是Journey的举一反三,只不过在这里没有告诉你k是多少且没有了边权而已。

那么问题来了:我们该怎么求出k的多少呢?暴力枚举k吗?

no!

我们来看一下第二个样例:

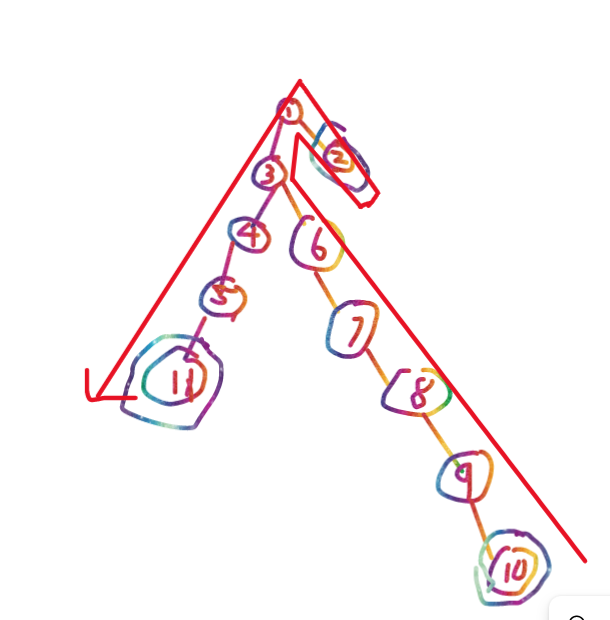
在这里划红的线为遍历时的路径。

那么此时我们发现:起点k为10，也就是深度最深的那个必须要走过的节点!

那么此时我们会有有一个大胆的猜想:会不会在这道题中k就是深度最深的那个必须要走过的节点呢?

我们来试着证明一下上面的猜想:在这里如果深度最深的那个必须要走过的节点是中途遇到的,那么我们还要返回到根,而返回的距离是非常长的(因为该节点深度最深)，那么得到的一定不是最优解,而以深度最深的那个必须要走过的节点为k的话就不用再往返2次了，大大的减少了距离。

---

三,代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
/*
pre[j]:对于第i条边来说，它的上一条边是哪一条边
now[x]:对于点x来说，最后一条描述它充当父结点的边是哪一条边
son[i]:在第i条边中，充当子结点的点是哪一个
*/
int eg,pre[1000001],now[1000001],ans,son[1000001],vis[1000001],n,k,s,dep[1000001],q,jll[1000001],mk;
void dfs(int u,int fa,int d)
{
  dep[u] = d;
  for(int i = now[u];i;i = pre[i])
  {
      int v = son[i];
      if(v == fa) continue;
      dfs(v,u,d + 1);
      if(vis[v] == 1)
      {
        s += 2 * 1;
        vis[u] = 1;
    }
  }
}
void d(int beg,int fa,int nw)
{
  jll[beg] = nw;
  for(int i = now[beg]; i; i = pre[i])
    if(son[i] != fa)
      d(son[i],beg,nw + 1);
}
void adeg(int u,int v)
{
  pre[++eg] = now[u];
  now[u] = eg;
  son[eg] = v;
}
signed main()
{
  cin>>n>>q;
  for(int i = 1;i < n;i++)
  {
      int u,v,w;
      cin>>u>>v;
      adeg(u,v);
      adeg(v,u);
  }
  int x;
  for(int i = 1;i <= q;i++)
  {
      cin>>x;
      vis[x] = 1;
  }
  d(1,0,0);
  for(int i = 1;i <= n;i++)
    if(mk < jll[i] && vis[i] == 1)
    {
      k = i;
      mk = jll[i];
    }
  dfs(k,0,0);
  for(int i = 1;i <= n;i++)
    if(vis[i])
      ans = max(ans,dep[i]);
  cout<<s - ans;
  return 0;
}