前言

思路及算法思维，指路 代码随想录。
题目来自 LeetCode。

day 15，一周中最困难的周三~

题目详情

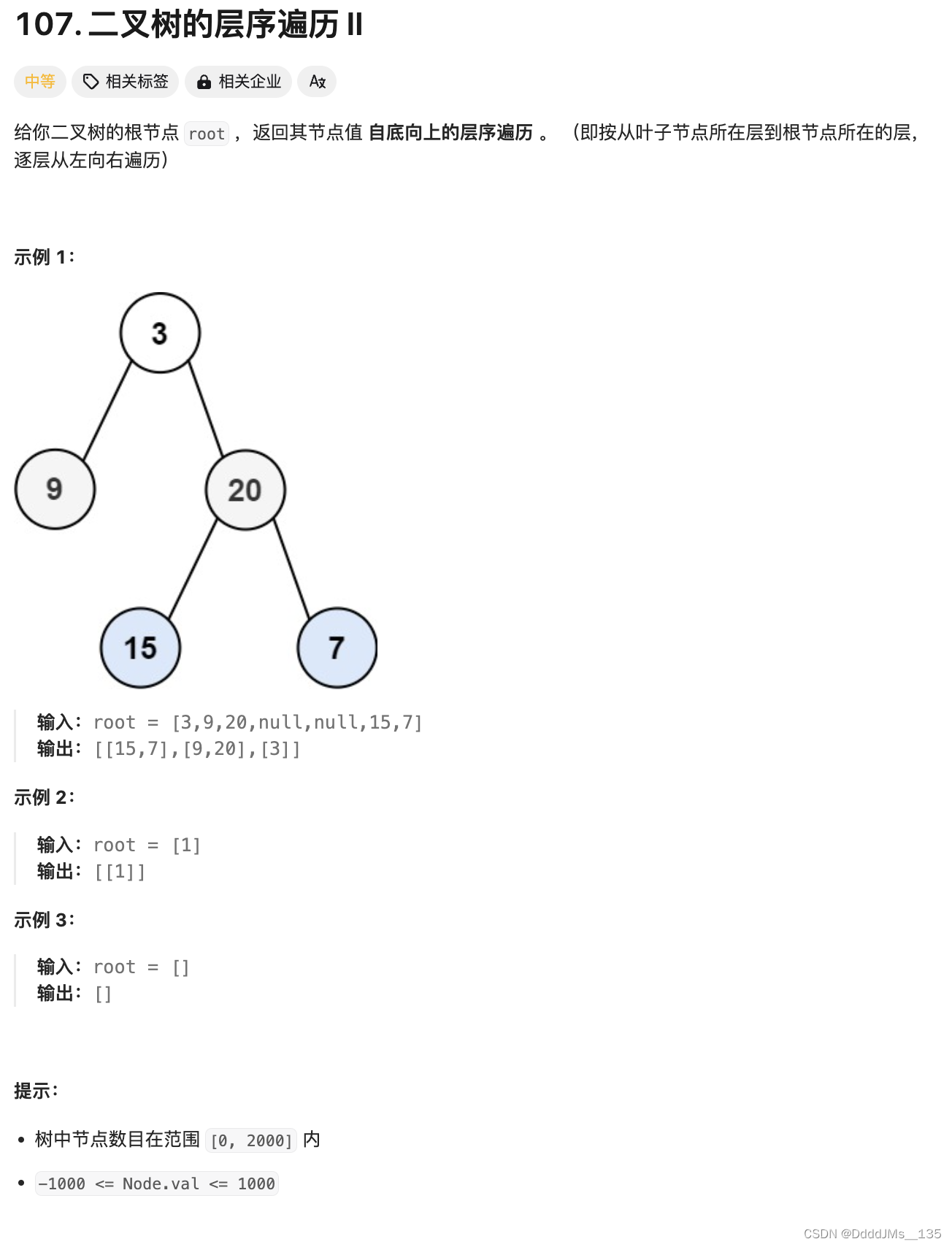
[102] 二叉树的层序遍历

题目描述

102 二叉树的层序遍历

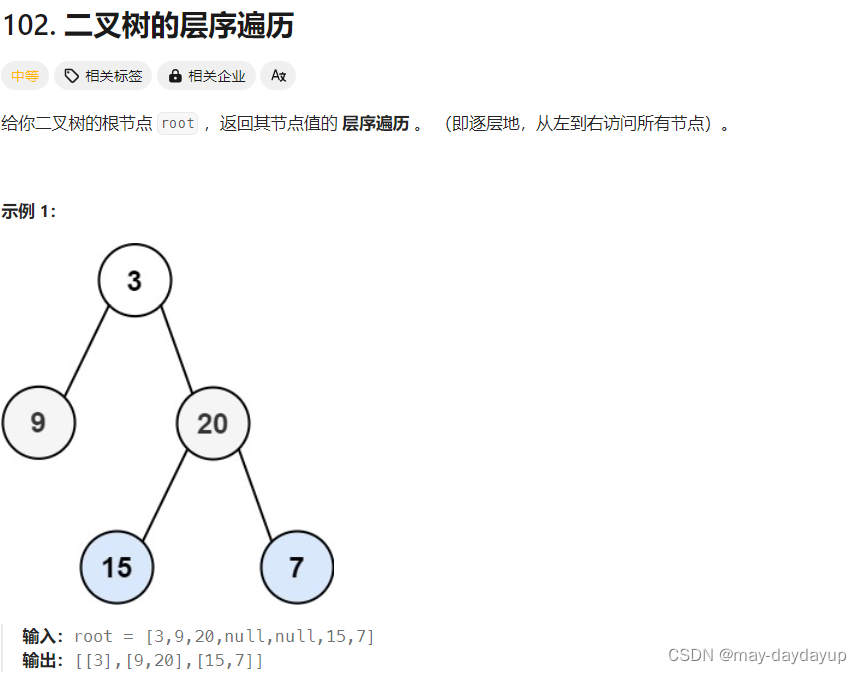
解题思路

前提：二叉树的层级遍历
思路：利用队列的“先进先出”特性，层级遍历二叉树。
重点：利用队列的“先进先出”特性，层级遍历二叉树。

代码实现

C语言

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes) {
    //输出结果初始化
    *returnSize = 0;

    // 空结点
    if (root == NULL)
    {
        return NULL;
    }
    
    int **ret = NULL;
    struct TreeNode *queue[2000];
    int idx = 0;
    int start = 0;
    queue[idx++] = root;
    while (start < idx)
    {
        // 动态分配输出数组大小
        (*returnSize)++;
        ret = (int **)realloc(ret, sizeof(int *) * (*returnSize));
        *returnColumnSizes = (int *)realloc(*returnColumnSizes, sizeof(int) * (*returnSize));
        (*returnColumnSizes)[(*returnSize) - 1] = idx - start;
        ret[(*returnSize) - 1] = (int *)malloc(sizeof(int) * ((*returnColumnSizes)[(*returnSize) - 1]));
        // 输出该层结点
        for (int i = 0; i < (*returnColumnSizes)[(*returnSize) - 1]; i++)
        {
            struct TreeNode *cur = queue[start++];
            // 左结点压栈
            if (cur->left)
            {
                queue[idx++] = cur->left;
            }
            // 右结点压栈
            if (cur->right)
            {
                queue[idx++] = cur->right;
            }
            // 输出该结点
            ret[(*returnSize) - 1][i] = cur->val;
        }
    }
    return ret;
}

[226] 翻转二叉树

题目描述

226 翻转二叉树

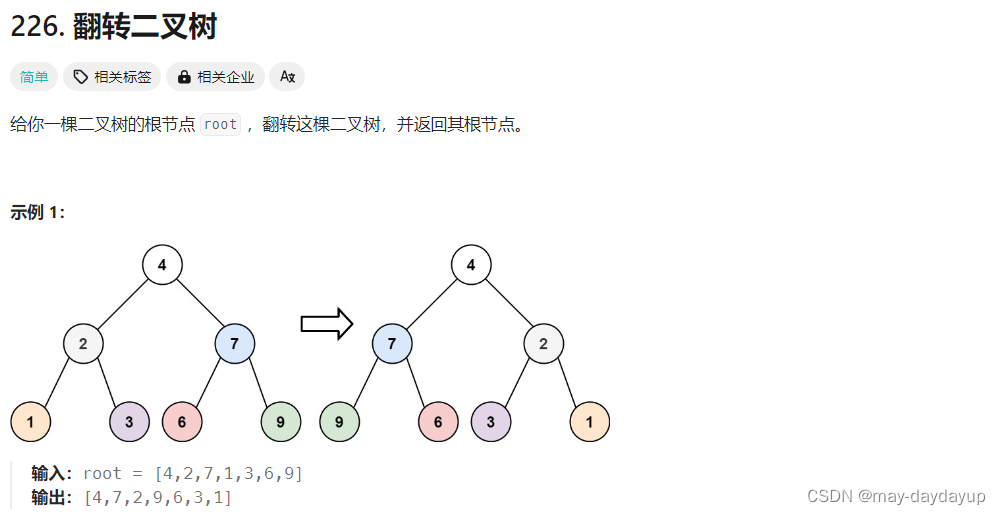
解题思路

前提：翻转二叉树，左右子树结点位置交换
思路：从上到下，左右子树位置交换，可以采用先序或者后序遍历。
重点：无法使用中序遍历，中序遍历会使二叉树反转两次，变成原二叉树。

代码实现

C语言

先序遍历 递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
void reversalTree(struct TreeNode *root)
{
    if (root == NULL)
    {
        return ;
    }
    // 左右结点反转
    struct TreeNode *tmp = root->left;
    root->left = root->right;
    root->right = tmp;
    reversalTree(root->left);
    reversalTree(root->right);
    return ;
}

struct TreeNode* invertTree(struct TreeNode* root) {
    reversalTree(root);
    return root;
}

先序遍历 迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* invertTree(struct TreeNode* root) {
    struct TreeNode *stack[100];
    int idx = 0;
    if (root != NULL)
    {
        stack[idx++] = root;
    }
    while (idx > 0)
    {
        
        struct TreeNode *cur = stack[--idx];
        // 左右结点非空入栈
        if (cur->left)
        {
            stack[idx++] = cur->left;
        }
        if (cur->right)
        {
            stack[idx++] = cur->right;
        }
        // 交换左右结点
        struct TreeNode *tmp = cur->left;
        cur->left = cur->right;
        cur->right = tmp;
    }
    return root;
}

[101] 对称二叉树

题目描述

101 对称二叉树

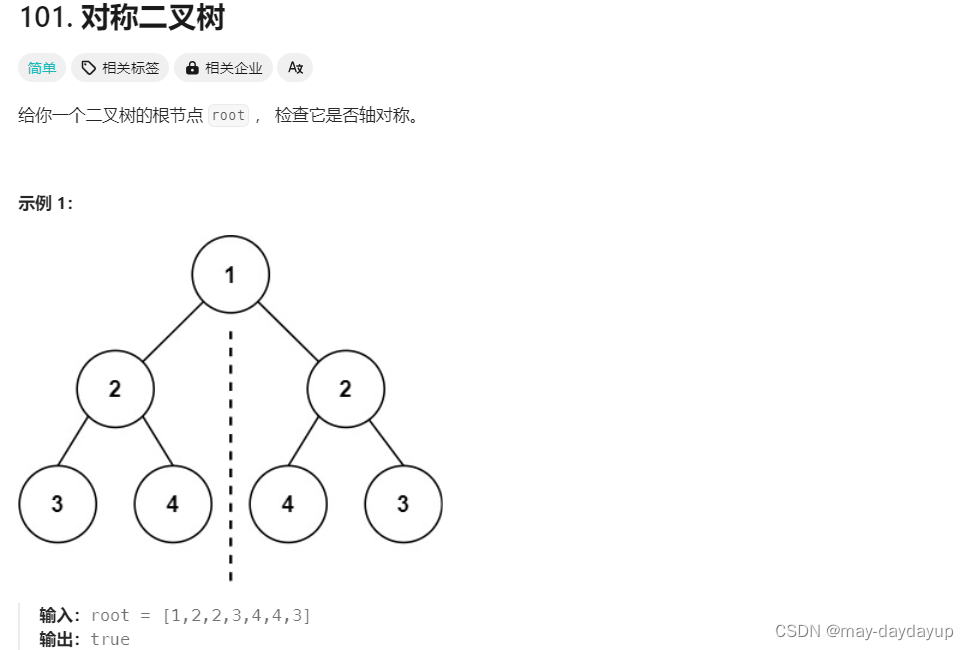
解题思路

前提：二叉树左右子树镜像对称
思路：先序遍历、层级遍历均可以实现。
重点：判断结点相等的位置要明确。

代码实现

C语言

先序遍历 递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool isSymmetricFound(struct TreeNode* left, struct TreeNode* right)
{
    if ((left == NULL) && (right == NULL))
    {
        return true;
    }
    else if (((left != NULL) && (right == NULL)) || ((left == NULL) && (right != NULL)))
    {
        return false;
    }
    else if (left->val != right->val)
    {
        return false;
    }
    // 递归
    bool ans = false;
    ans = isSymmetricFound(left->left, right->right);
    if (ans != true)
    {
        return false;
    }
    return isSymmetricFound(left->right, right->left);
}

bool isSymmetric(struct TreeNode* root) {
    // 判断空树
    if (root == NULL)
    {
        return true;
    }
    return isSymmetricFound(root->left, root->right);
}

先序遍历 迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSymmetric(struct TreeNode* root) {
    // 判断空树
    if (root == NULL)
    {
        return true;
    }
    // 使用栈(队列同样的处理流程)
    struct TreeNode *stack[1000];
    int idx = 0;
    // left right成对入栈，即使为null
    stack[idx++] = root->right;
    stack[idx++] = root->left;
    while (idx)
    {
        struct TreeNode *left = stack[--idx];
        struct TreeNode *right = stack[--idx];
        if ((left == NULL) && (right == NULL))
        {
            continue;
        }
        else if (((left != NULL) && (right == NULL)) || ((left == NULL) && (right != NULL)))
        {
            return false;
        }
        else if (left->val != right->val)
        {
            return false;
        }
        // 此时左右结点均为非空，将该左右结点的子节点 成对 入栈
        stack[idx++] = right->right;
        stack[idx++] = left->left;
        stack[idx++] = left->right;
        stack[idx++] = right->left;
    }
    return true;
}

层级遍历

同先序遍历 迭代，只是将stack换为 queue，实现流程一致。

今日收获

1. 二叉树的遍历，递归及迭代的实现。