题目链接
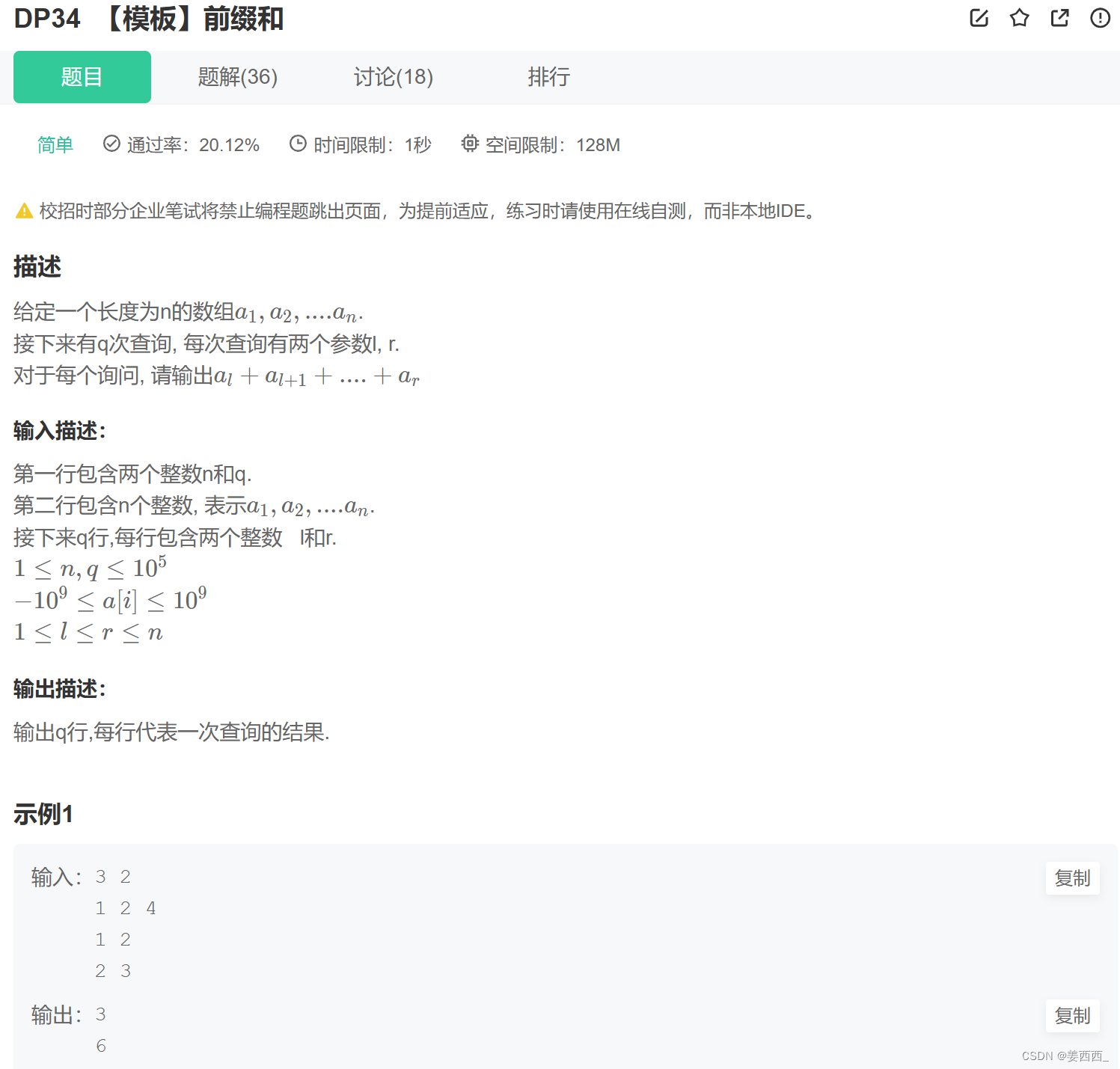
题目:
分析:
- 因为要求数组中连续区间的和, 可以使用前缀和算法
- 注意:下标是从1开始算起的, 真正下标0的位置是0
- 第一步:
预处理出来一个前缀和数组dp
dp[i] 表示: 表示[1,i] 区间所有元素的和
dp[i] = dp[i-1] + arr[i] - 例如示例一中: dp数组为{1,3,7}
- 第二步: 使用前缀数组
要求[l,r]区间的和 = dp[r] - dp[l-1] - 例如示例一中: 求[1,2]的和 = dp[2] - dp[0] = 3
- 疑问: 为什么我们的下标要从1开始计数呢?
为了处理边界情况
如果从0开始, 那么计算dp[i]时, dp[0] = dp[-1] + arr[0] 会出现越界, 并且在计算[0,2]的区间和时, dp[2] - dp[-1] 也会出现越界, 那么从下标从1开始计数就很好的规避了这个问题, 计算dp[i]时, dp[1] = dp[0] + arr[1], dp[0]的位置我们并没有管, 所以还是0, 那么dp[1] = arr[1]正确, 在计算[1,2]的区间和时, dp[2] - dp[0] = dp[2], 正确
代码:
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int q = in.nextInt();
int[] arr = new int[n+1];
for(int i = 1;i < n+1;i++){
arr[i] = in.nextInt();
}
long[] dp = new long[n+1];
for(int i = 1;i < n+1;i++){
dp[i] = dp[i-1] + arr[i];
}
while(q>0){
int l = in.nextInt();
int r = in.nextInt();
System.out.println(dp[r] - dp[l - 1]);
q--;
}
}
}