背景
除了生成各种奇形怪状与自然景观,噪声也有其他美妙的用途!
工作原因,经常接触与噪声相关的画面效果(火焰啊,画面扰动啊之类的),做的时候一知半解,傻傻分不清楚各种形态的noise,也不知道三维noise和二维noise的具体区别,只知道在shadertoy上找到相似的噪声然后ctrl c/v一下,特别是在具体的业务场景中,比如设计需要这种形态的火焰,需要那种形态的画面扰动,对我来说简直是挠破了脑袋,噪声调半天都不一定能调出一个满意的结果😂
刚好近期的工作需要分析ae的效果控件【分形杂色】【湍流杂色】,找到一篇原作者对【分形杂色】效果原理的说明,再次引起了对噪声的兴趣,也更希望能啃啃这块软骨!
因此有了这篇文档,是我对各种噪声的学习理解,(有时间的话)下篇再来展示下各种噪声的(画面上的)应用,名字我都想好了!就叫【猴子都会使用的噪声(noise)专题】🤣
前提
接下来的所有代码都能在shadertoy上运行,下面的图像也基本都生成于shadertoy
参考的各种资料文档,也会在相应地方提供出处,但不用阅读出处的具体细节,也能理解本篇的内容!(自信)
由于还是有些内容没理解明白,所以会有一些问题会以斜体引用的形式出现在文档中,用来质问愚蠢的自己,希望自己未来能解决掉提出的问题吧,也希望如果有好哥哥知道答案,能在评论区中留下你的箴言,赞美太阳☀!
(例子)呐,莱纳,为什么妈妈会被巨人吃掉呢?
Hash/White Noise(杂乱/白噪声)
在shadertoy中涉及噪声相关的效果,都不难发现有hash函数(有时候是random函数),再参考一下wiki对white noise的描述(实际上white noise的定义会更加广泛,不局限于图像中),也跟hash函数产生的图像极其相似,所以这里把hash跟white放在一块
不太理解这函数为啥叫hash,而不是white,还是我理解错了hash跟white不能划等号
对于图像来说,每个像素都有其位置,即uv,把uv作为hash函数的输入,可以得到伪随机的结果
这里hash函数的实现挺自由的,各种magic number,而且用到dot,fract,sin等函数或是这些函数的组合,虽然出来的结果大同小异,但还是有些区别的,特别是利用sin作为hash的实现,在放大uv的时候会有规律性的artifact
参考:生成Sinhash和Fracthash Noise
参考上文的实践,建议还是用dot/fract作为hash的实现,如果用带有sin的hash函数,接下来的噪声实现在uv放大后都有周期性的表现,而且在不同的机子中(比如安卓/ios)由于高频下精度不同会导致sin函数输出的结果有差异,可能会有不同设备输出结果不一致的问题
float hash(vec2 p) { vec3 p3 = fract(vec3(p.xyx) * .1031); p3 += dot(p3, p3.yzx + 33.33); return fract((p3.x + p3.y) * p3.z); }
float hash_with_sin(vec2 _st) { return fract(sin(dot(_st.xy, vec2(12.9898,78.233)))*43758.5453123); }
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord/iResolution.xy;
float i = floor(uv.x);
float scale = 1000.; // 尝试放大这个值,会发现hash_with_sin与hash的区别
vec3 col = vec3(random(uv*scale + iTime*0.001))*step(.5, uv.x);//RIGHT
vec3 colsin = vec3(randomSin(uv*scale + iTime*0.001))*(1.-step(.5, uv.x));//LEFT
vec3 line = vec3(smoothstep(.5, .5, uv.x)) - vec3(smoothstep(.51, .51, uv.x));
// Output to screen
fragColor = vec4(col + colsin + line,1.0);
}

左hash_with_sin,右hash,就算是观察静止的图片也能看到左边呈现一些规律性,如果加上iTime会更加明显
参考另外一个链接的hash库,无敌了:【shader】超级噪声库,附代码(fbm、Perlin、Simplex、Worley、Tiling、Curl等,很全很全)
hash库,不用纠结具体怎么实现,里面的magic number也不需要额外关心,随意就行
float hash11(float p) { p = fract(p * .1031); p *= p + 33.33; p *= p + p; return fract(p); }
float hash21(vec2 p) { vec3 p3 = fract(vec3(p.xyx) * .1031); p3 += dot(p3, p3.yzx + 33.33); return fract((p3.x + p3.y) * p3.z); }
float hash31(vec3 p3) { p3 = fract(p3 * .1031); p3 += dot(p3, p3.zyx + 31.32); return fract((p3.x + p3.y) * p3.z); }
vec2 hash12(float p) { vec3 p3 = fract(vec3(p) * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yzx + 33.33); return fract((p3.xx+p3.yz)*p3.zy); }
vec2 hash22(vec2 p) { vec3 p3 = fract(vec3(p.xyx) * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yzx+33.33); return fract((p3.xx+p3.yz)*p3.zy); }
vec2 hash32(vec3 p3) { p3 = fract(p3 * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yzx+33.33); return fract((p3.xx+p3.yz)*p3.zy); }
vec3 hash13(float p) { vec3 p3 = fract(vec3(p) * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yzx+33.33); return fract((p3.xxy+p3.yzz)*p3.zyx); }
vec3 hash23(vec2 p) { vec3 p3 = fract(vec3(p.xyx) * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yxz+33.33); return fract((p3.xxy+p3.yzz)*p3.zyx); }
vec3 hash33(vec3 p3){ p3 = fract(p3 * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yxz+33.33); return fract((p3.xxy + p3.yxx)*p3.zyx); }
vec4 hash14(float p) { vec4 p4 = fract(vec4(p) * vec4(.1031, .1030, .0973, .1099)); p4 += dot(p4, p4.wzxy+33.33); return fract((p4.xxyz+p4.yzzw)*p4.zywx); }
vec4 hash24(vec2 p) { vec4 p4 = fract(vec4(p.xyxy) * vec4(.1031, .1030, .0973, .1099)); p4 += dot(p4, p4.wzxy+33.33); return fract((p4.xxyz+p4.yzzw)*p4.zywx); }
vec4 hash34(vec3 p) { vec4 p4 = fract(vec4(p.xyzx) * vec4(.1031, .1030, .0973, .1099)); p4 += dot(p4, p4.wzxy+33.33); return fract((p4.xxyz+p4.yzzw)*p4.zywx); }
vec4 hash44(vec4 p4) { p4 = fract(p4 * vec4(.1031, .1030, .0973, .1099)); p4 += dot(p4, p4.wzxy+33.33); return fract((p4.xxyz+p4.yzzw)*p4.zywx); }
Value Noise(值噪声)
上面的hash noise是对每个像素过hash函数,所以出来的图像是个雪花
倘若我们不对每个像素做呢?如果我们对uv做类似马赛克一样的处理,比如10x10个像素作为一个单位拿去过hash函数会怎么样捏?
这10x10个像素组成一个正方形,称作一个晶格,这个晶格(正方形)存在四个顶点,每个顶点拿去过hash函数能得到不同的随机值,晶格中每个像素的输出则由这四个顶点的随机值与该像素的位置决定👇

float hash21(vec2 p) { vec3 p3 = fract(vec3(p.xyx) * .1031); p3 += dot(p3, p3.yzx + 33.33); return fract((p3.x + p3.y) * p3.z); }
float value_noise(vec2 p){
vec2 pi = floor(p);
vec2 pf = p - pi;
vec2 w = pf;
// vec2 w = pf * pf * (3.0 - 2.0 * pf);
return mix(mix(hash21(pi + vec2(0.0, 0.0)), hash21(pi + vec2(1.0, 0.0)), w.x),
mix(hash21(pi + vec2(0.0, 1.0)), hash21(pi + vec2(1.0, 1.0)), w.x),
w.y);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (fragCoord-iResolution.xy)/iResolution.y;
float n = value_noise(uv*10.);
vec3 col = vec3(n);
fragColor = vec4(col,1.0);
}
可以看到图像呈现方方正正的晶格,上面的插值只是简单的线性插值,也就是上面的vec2 w = pf;
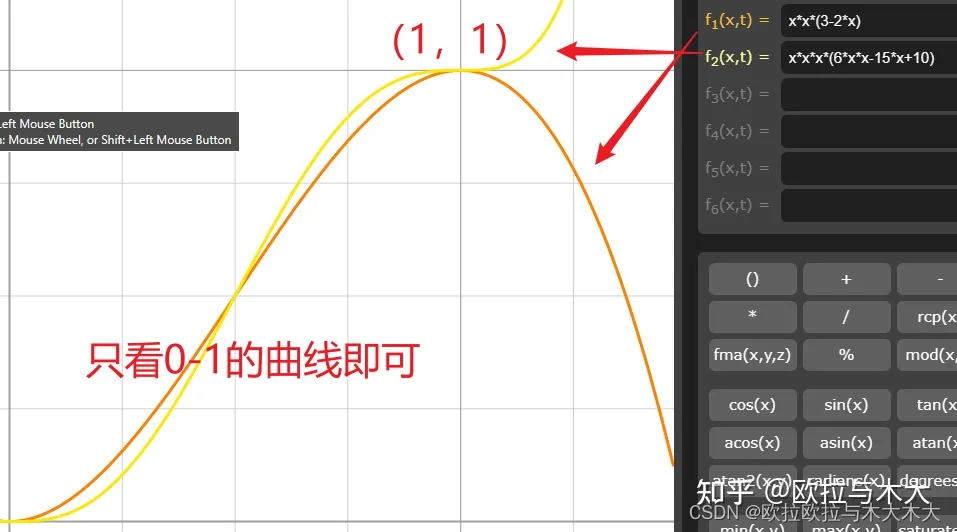
改造这个插值函数会有不一样的体验,换成vec2 w = pf * pf * (3.0 - 2.0 * pf);会舒缓多,但晶格的感觉还是存在


这个插值函数的改造十分重要!后续存在感超高!
Perlin Noise(经典噪声)
参考:https://en.wikipedia.org/wiki/Perlin_noise
为了解决value noise的晶格块状感,Ken Perlin大神开发了Gradient Noise,其思想非常朴素
- 晶格的四个点输出一个二维的noise,而不是像值噪声一样输出个一维的noise
- 参考value noise的插值范围由第一步生成的二维noise与该像素点的位置决定
这里也解释了为啥value noise是一块一块的了,因为在mix(a,b,x)中,value noise的ab对于晶格中的每个像素都是一样的,所以出来的结果呈现“块”的规律性,而gradient noise的做法则是让晶格中每个像素的计算中的ab值有所不同,出来的结果会更“润滑”一点
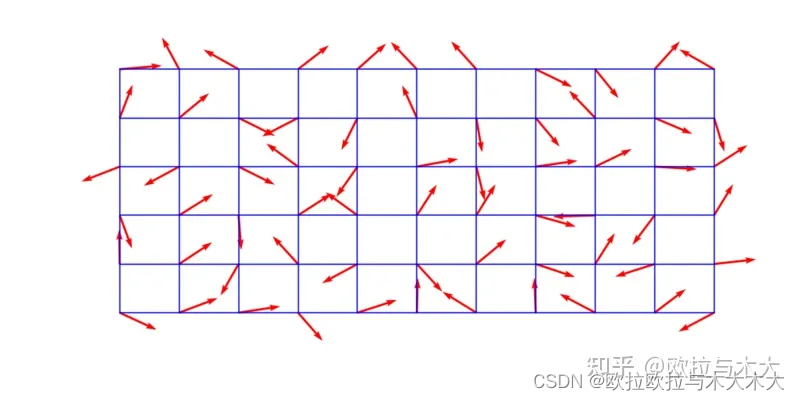
我个人感觉value noise也可以算是利用梯度生成的函数,四个顶点也算是相邻晶格的值嘛,不知道为啥value
noise并不归类为gradient noise大家庭中。。
其中perlin noise则是gradient noise最经典,最广为人知的noise算法了,其做法是让晶格中四个顶点所生成的二维noise与像素点的距离进行点乘
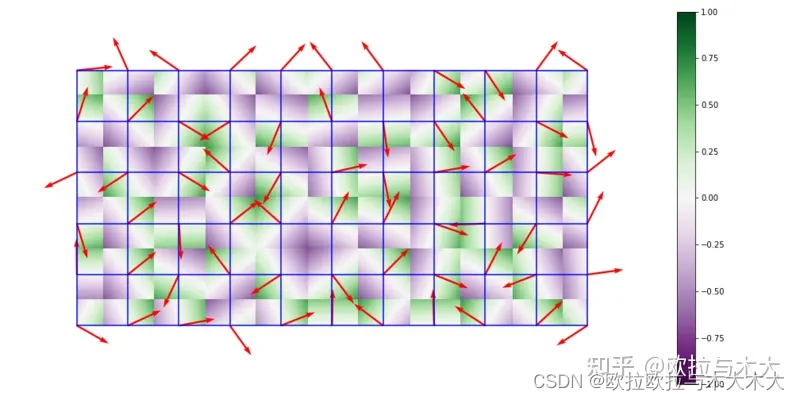
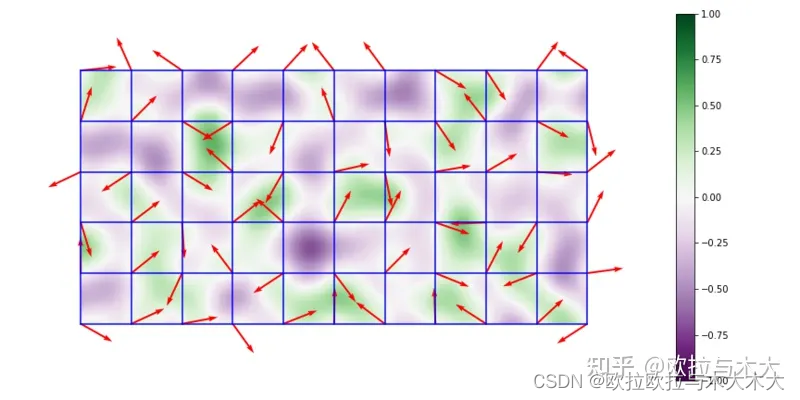
vec2 hash22(vec2 p){ p = vec2( dot(p,vec2(127.1,311.7)), dot(p,vec2(269.5,183.3))); return -1.0 + 2.0 * fract(sin(p)*43758.5453123); }
float perlin_noise(vec2 p){
vec2 pi = floor(p);
vec2 pf = p - pi;
vec2 w = pf * pf * (3.0 - 2.0 * pf);
//vec2 w = pf * pf * pf * (6.*pf*pf-15.*pf+10.);
return mix(mix(dot(hash22(pi + vec2(0.0, 0.0)), pf - vec2(0.0, 0.0)),
dot(hash22(pi + vec2(1.0, 0.0)), pf - vec2(1.0, 0.0)), w.x),
mix(dot(hash22(pi + vec2(0.0, 1.0)), pf - vec2(0.0, 1.0)),
dot(hash22(pi + vec2(1.0, 1.0)), pf - vec2(1.0, 1.0)), w.x),
w.y);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (fragCoord-iResolution.xy)/iResolution.y;
float n = perlin_noise(uv*10.);
n = n * 0.5 + 0.5;
vec3 col = vec3(n);
fragColor = vec4(col,1.0);
}
同样的,插值函数也发现有更平滑的优化

Simplex Noise(优化的Perlin Noise)
参考 :https://en.wikipedia.org/wiki/Simplex_noise
在二维图像中,无论上面的value noise还是perlin noise,都是用拥有四个顶点的晶格来作为单位进行插值
让我们进行逆二向箔打击,上升到三维来思考,想象一下对二维图像做一个挤出操作,晶格就变成了正方体,构成这个正方体的最小单位将其称为体素,现在每个体素都要有属于自己的noise值,这时候要怎么插值呢?
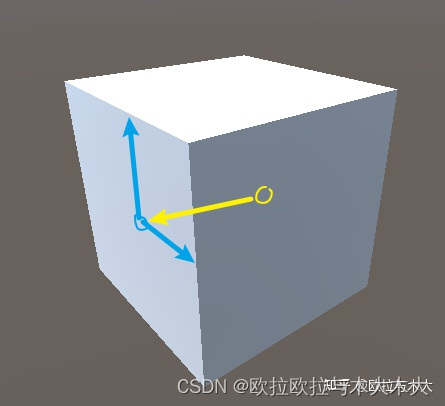
观察上图,虽然只是多了一个维度,但插值的计算会涉及八个点,即正方体的八个点
计算出八个点的一维/二维noise值,再根据体素的位置(x,y,z)进行插值,完成value/perlin noise的计算
看着计算量好像也不大,但如果上升到四维,五维,甚至n维呢,n维的超立方体有2n个点,用经典perlin计算下来的复杂度是O(n2n),不太划算
换个角度,假如不用四边形晶格来计算,而是用三角形呢
先假设图像里都用三角形来构建晶格成功了,那对图像做挤出操作上升到三维,那构成这个立方体的“晶格”单位则是四边体,对应的n维则是n+1个点,复杂度降低为O(2n)
参考iq大佬对2d/3d simplex nosie的实现
vec2 hash22(vec2 p) { vec3 p3 = fract(vec3(p.xyx) * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yzx+19.19); return -1. + 2.*fract((p3.xx+p3.yz)*p3.zy); }
/* 2d simplex noise */
float simplex2d(vec2 p) {
const float K1 = 0.366025404; // (sqrt(3)-1)/2;
const float K2 = 0.211324865; // (3-sqrt(3))/6;
vec2 i = floor( p + (p.x+p.y)*K1 );
vec2 a = p - i + (i.x+i.y)*K2;
float m = step(a.y,a.x);
vec2 o = vec2(m,1.0-m);
vec2 b = a - o + K2;
vec2 c = a - 1.0 + 2.0*K2;
vec3 h = max( 0.5-vec3(dot(a,a), dot(b,b), dot(c,c) ), 0.0 );
vec3 n = h*h*h*h*vec3( dot(a,hash22(i+0.0)), dot(b,hash22(i+o)), dot(c,hash22(i+1.0)));
return dot( n, vec3(70.0) );
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (1.0*fragCoord-iResolution.xy)/iResolution.y;
float n = simplex2d(uv*10.);
//n = n * 0.5 + 0.5;
vec3 col = vec3(n);
fragColor = vec4(col,1.0);
}


下面是3d simplex noise的实现,因为没太关注他的“3d晶格”是怎么构建的,所以就直接去掉注释了,想推导的可以看看里面的具体内容
vec3 hash33(vec3 p3){ p3 = fract(p3 * vec3(.1031, .1030, .0973)); p3 += dot(p3, p3.yxz+33.33); return fract((p3.xxy + p3.yxx)*p3.zyx); }
/* skew constants for 3d simplex functions */
const float F3 = 0.3333333;
const float G3 = 0.1666667;
/* 3d simplex noise */
float simplex3d(vec3 p) {
vec3 s = floor(p + dot(p, vec3(F3)));
vec3 x = p - s + dot(s, vec3(G3));
vec3 e = step(vec3(0.0), x - x.yzx);
vec3 i1 = e*(1.0 - e.zxy);
vec3 i2 = 1.0 - e.zxy*(1.0 - e);
vec3 x1 = x - i1 + G3;
vec3 x2 = x - i2 + 2.0*G3;
vec3 x3 = x - 1.0 + 3.0*G3;
vec4 w, d;
w.x = dot(x, x);
w.y = dot(x1, x1);
w.z = dot(x2, x2);
w.w = dot(x3, x3);
w = max(0.6 - w, 0.0);
d.x = dot(hash33(s)-0.5, x);
d.y = dot(hash33(s + i1)-0.5, x1);
d.z = dot(hash33(s + i2)-0.5, x2);
d.w = dot(hash33(s + 1.0)-0.5, x3);
w *= w;
w *= w;
d *= w;
return dot(d, vec4(52.0));
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (2.0*fragCoord-iResolution.xy)/iResolution.y;
uv *= 10.;
float n = simplex3d(vec3(uv.xy, iTime));
n = n * 0.5 + 0.5;
vec3 col = vec3(n);
fragColor = vec4(col,1.0);
}
FBM(Fractal Brownian Motion,分型布朗运动)
参考:https://thebookofshaders.com/13/?lan=ch
其实没啥好讲的,就是好几个noise的叠加,这里不是指white noise,而是指value/perlin/simplex这些noise的叠加
基于此叠加的规矩也会有所不同,出来的结果还是挺有意思的,这里就不赘述了背景
除了生成各种奇形怪状与自然景观,噪声也有其他美妙的用途!