目录
- 1 视线引导法介绍
- 2 LOS制导原理推导
- 3 Lyapunov稳定性分析
- 4 LOS制导效果
1 视线引导法介绍
视线引导法(Line of Sight, LOS)作为无人水面艇(USV)自主导航领域的核心技术,通过几何制导与动态控制深度融合的机制,为复杂海洋环境下的高精度路径跟踪提供了鲁棒性解决方案。其核心原理建立在运动学几何投影与闭环反馈控制的双重架构上:系统实时计算无人船当前位置与预设航路点之间的视线角,通过航向控制器动态调整船体艏摇角使其精确对准该视线方向,同时配合自适应航速策略,形成兼具轨迹跟踪精度与运动稳定性的制导体系。

为实现视线角的精确跟踪,LOS制导与航向控制器形成级联控制架构:LOS制导系统首先根据全局路径规划生成的航路点序列构建虚拟参考路径,在每个控制周期内选取距离船体最近的路径点作为当前跟踪目标,通过几何投影建立船体坐标系与惯性坐标系间的空间映射关系,计算得到视线角 ψ l o s \psi_{los} ψlos,从而生成期望航向指令 ψ d \psi_{d} ψd,内环控制层则基于航向偏差 e ψ p ˉ s i d − ψ e_\psi\=psi_{d}-\psi eψpˉsid−ψ,通过控制算法输出转艏力矩τ_r,驱动推进系统调整船体方向,如下图所示

2 LOS制导原理推导
如图所示为LOS制导几何关系示意图
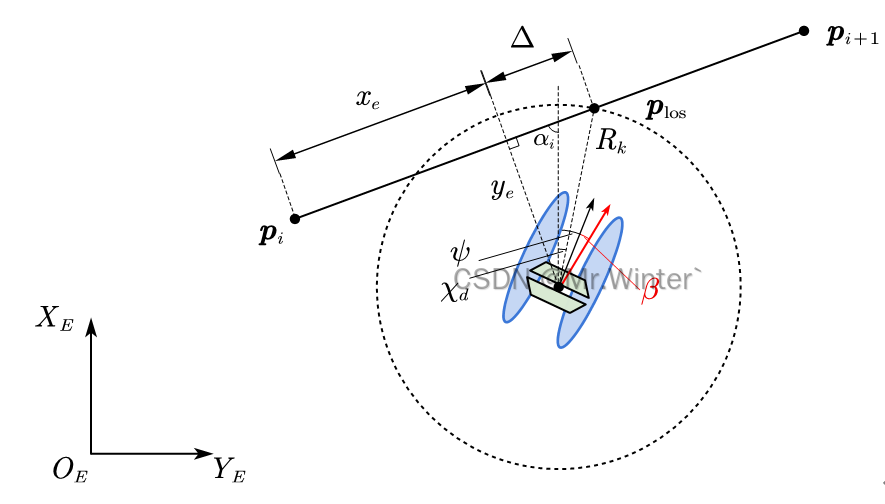
设上一个路点为 p i \boldsymbol{p}_i pi,下一个路点为 p i + 1 \boldsymbol{p}_{i+1} pi+1,USV当前位置为 p = [ x y ] T \boldsymbol{p}=\left[ \begin{matrix} x& y\\\end{matrix} \right] ^T p=[xy]T。以 p \boldsymbol{p} p为圆心作半径为 R k R_k Rk的圆交直线段 p i p i + 1 \boldsymbol{p}_i\boldsymbol{p}_{i+1} pipi+1于两点,距离下一个路点 p i + 1 \boldsymbol{p}_{i+1} pi+1较近的交点为当前跟踪的期望路点 p l o s \boldsymbol{p}_{\mathrm{los}} plos。定义前视距离 Δ \Delta Δ为USV在当前段路径投影点与LOS制导点 p l o s \boldsymbol{p}_{\mathrm{los}} plos的前向距离,在静态LOS制导律中, Δ \Delta Δ或 R k R_k Rk为定值(已知 Δ \Delta Δ或 R k R_k Rk中的一项可以求出另一项),一般设为USV长度 L L L的 n n n倍,即
Δ = n L \Delta =nL Δ=nL
由几何关系可得横纵向跟踪误差
{ x e = ( x − x i ) cos α i + ( y − y i ) sin α i y e = − ( x − x i ) sin α i + ( y − y i ) cos α i \begin{cases} x_e=\left( x-x_i \right) \cos \alpha _i+\left( y-y_i \right) \sin \alpha _i\\ y_e=-\left( x-x_i \right) \sin \alpha _i+\left( y-y_i \right) \cos \alpha _i\\\end{cases} {xe=(x−xi)cosαi+(y−yi)sinαiye=−(x−xi)sinαi+(y−yi)cosαi
其中 α i = a r c tan ( ( y i + 1 − y i ) / ( x i + 1 − x i ) ) \alpha _i=\mathrm{arc}\tan \left( {{\left( y_{i+1}-y_i \right)}/{\left( x_{i+1}-x_i \right)}} \right) αi=arctan((yi+1−yi)/(xi+1−xi))。在USV运动过程中,受到风浪或自身驱动等因素影响将产生横向速度 v v v,使船艏不一定沿着航向行驶,艏向和航向的差角称为漂角
β = a r c tan ( v , u ) \beta =\mathrm{arc}\tan \left( v,u \right) β=arctan(v,u)
则USV当前航向角为 χ = ψ + β \chi =\psi +\beta χ=ψ+β,期望的航向角 χ d = α i − a r c tan ( y e / Δ ) \chi _d=\alpha _i-\mathrm{arc}\tan \left( {{y_e}/{\Delta}} \right) χd=αi−arctan(ye/Δ),令 χ = χ d \chi =\chi _d χ=χd可得
ψ d = α i − a r c tan ( y e / Δ ) − β \psi _d=\alpha _i-\mathrm{arc}\tan \left( {{y_e}/{\Delta}} \right) -\beta ψd=αi−arctan(ye/Δ)−β
即控制USV艏向为 ψ d \psi_d ψd时可使其沿着期望航向运动
3 Lyapunov稳定性分析
下来验证当采用 ψ = ψ d \psi=\psi_d ψ=ψd制导时可使横向误差收敛为零。求横向误差的一阶导数
y ˙ e = − x ˙ sin α i + y ˙ cos α i \dot{y}_e=-\dot{x}\sin \alpha _i+\dot{y}\cos \alpha _i y˙e=−x˙sinαi+y˙cosαi
根据运动学方程得到
y ˙ e = − ( u cos ψ − v sin ψ ) sin α i + ( u sin ψ + v cos ψ ) cos α i \dot{y}_e=-\left( u\cos \psi -v\sin \psi \right) \sin \alpha _i+\left( u\sin \psi +v\cos \psi \right) \cos \alpha _i y˙e=−(ucosψ−vsinψ)sinαi+(usinψ+vcosψ)cosαi
根据辅助角公式展开
y ˙ e = u 2 + v 2 sin ( ψ + β − α i ) \dot{y}_e=\sqrt{u^2+v^2}\sin \left( \psi +\beta -\alpha _i \right) y˙e=u2+v2sin(ψ+β−αi)
代入LOS制导律
y ˙ e = u 2 + v 2 sin ( − a r c tan ( y e / Δ ) ) = − u 2 + v 2 y e Δ 2 + y e 2 \begin{aligned} \dot{y}_e&=\sqrt{u^2+v^2}\sin \left( -\mathrm{arc}\tan \left( {{y_e}/{\Delta}} \right) \right) \\ &=-\sqrt{u^2+v^2}\frac{y_e}{\sqrt{\Delta ^2+y_{e}^{2}}}\end{aligned} y˙e=u2+v2sin(−arctan(ye/Δ))=−u2+v2Δ2+ye2ye
设Lyapunov函数
V = y e 2 2 V=\frac{y_{e}^{2}}{2} V=2ye2
则
V ˙ = − u 2 + v 2 y e 2 Δ 2 + y e 2 ⩽ 0 \dot{V}=-\sqrt{u^2+v^2}\frac{y_{e}^{2}}{\sqrt{\Delta ^2+y_{e}^{2}}}\leqslant 0 V˙=−u2+v2Δ2+ye2ye2⩽0
根据Lyapunov第二判据可知横向误差在LOS制导律下渐进稳定。
4 LOS制导效果
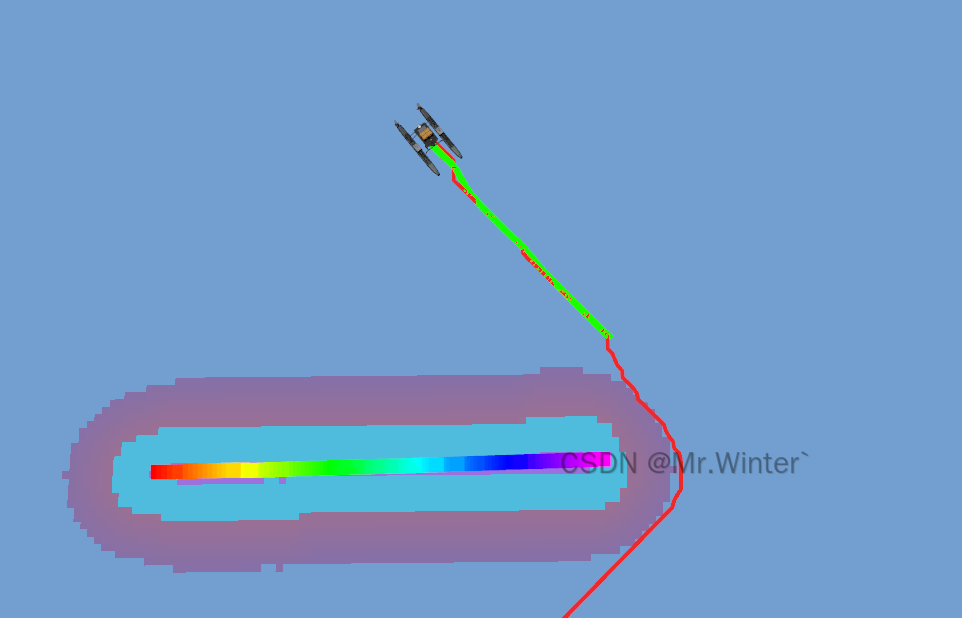
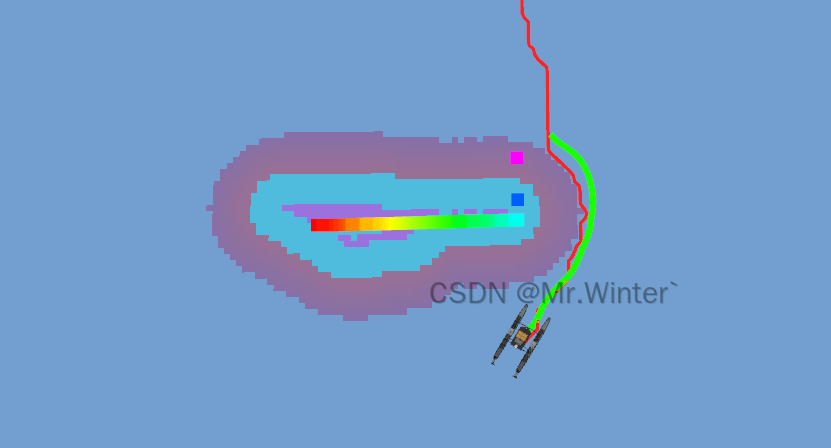
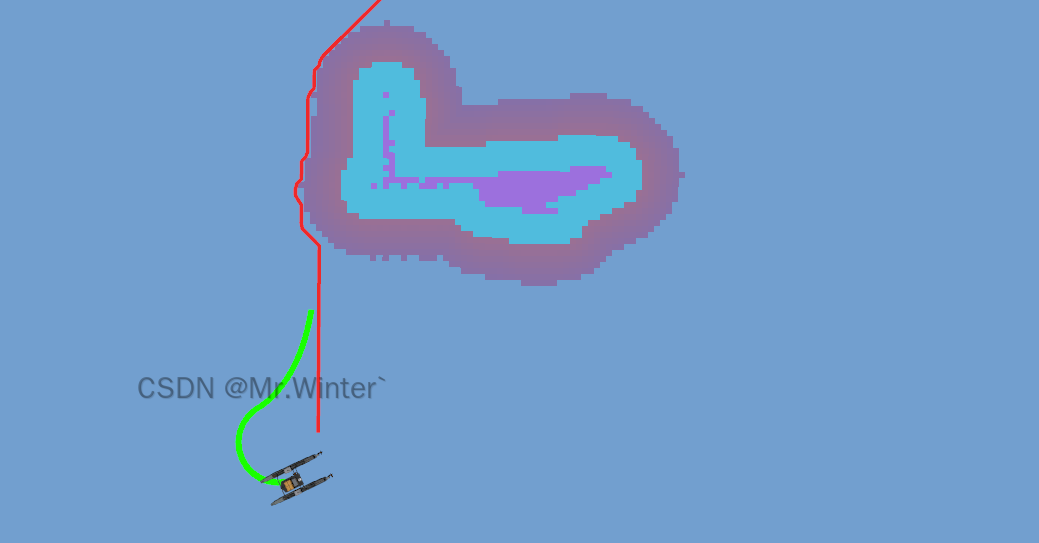
在下面的演示中,红色的是全局路径点,绿色的是LOS制导生成的模拟轨迹
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …



















