Problem

考虑一个线性方程组求解问题：
$$Ax=b\text{\hspace{1em}(1)}$$

其中，$A\in {\mathbb{R}}^{m\times n}$，$x\in {\mathbb{R}}^{n\times 1}$，$b\in {\mathbb{R}}^{m\times 1}$且$m\ll n$

这是一个欠定方程组，即该问题有无穷多解，那么如何添加一些约束，使得能够在这组无穷多解中找到一个最优的呢？

可以考虑一下稀疏性。

什么是稀疏性？通俗来讲，如果一个信号中仅有少量的大值，其余都是零，那么这个信号是稀疏的（或者说仅有少量的值相对于其他的值明显大得多）。稀疏性意味着信号是可压缩的，因为在数据表达时只需要考虑大值信号的位置和大小。

回到这个欠定方程组求解问题，如果待求解信号$x$是稀疏的，那么无穷多组解中找到最稀疏的那个解即为所求。该问题可以表达为一个$l_0$范数优化问题，即
$$min\parallel x{\parallel }_{0}s.t.Ax=b\text{\hspace{1em}(2)}$$

其中$\parallel x{\parallel }_0$表示$x$的0范数，即为$x$中非零值的个数，该问题是一个NP-hardness问题¹，求解相当困难。
幸运的是，当$A$与$b$满足RIP条件时²，问题(2)可以等价于求解一个$l_1$范数优化问题，即
$$min\parallel x{\parallel }_{1}s.t.Ax=b\text{\hspace{1em}(3)}$$

其中$\parallel x{\parallel }_1$表示$x$的1范数，即为$x$中元素的绝对值之和。该问题是一个凸优化问题，因此存在最优解。

$l_1$范数优化问题可以转化为一个标准的线性规划问题进行求解³，即
$$min{c}^T\theta s.t.\Phi \theta =s\text{\hspace{1em}(5)}$$

其中$c^T=[1,1,...,1],\theta =[u;v],\Phi =[A,-A],s=b$，注意：$c^T\in {\mathbb{R}}^{1\times 2n},\theta \in {\mathbb{R}}^{2n\times 1},\Phi \in {\mathbb{R}}^{m\times 2n},s\in {\mathbb{R}}^{m\times 1}$

最后$x=u-v$

Simulation⁴

M = 40;N = 100;K = 10;
x = zeros(N,1);
ind = randperm(N);  
x(ind(1:K)) = 10*randn(K,1);
A = randn(M,N);
b = A * x;
%% signal reconstruction
x0 = CS_linprog(A,b);
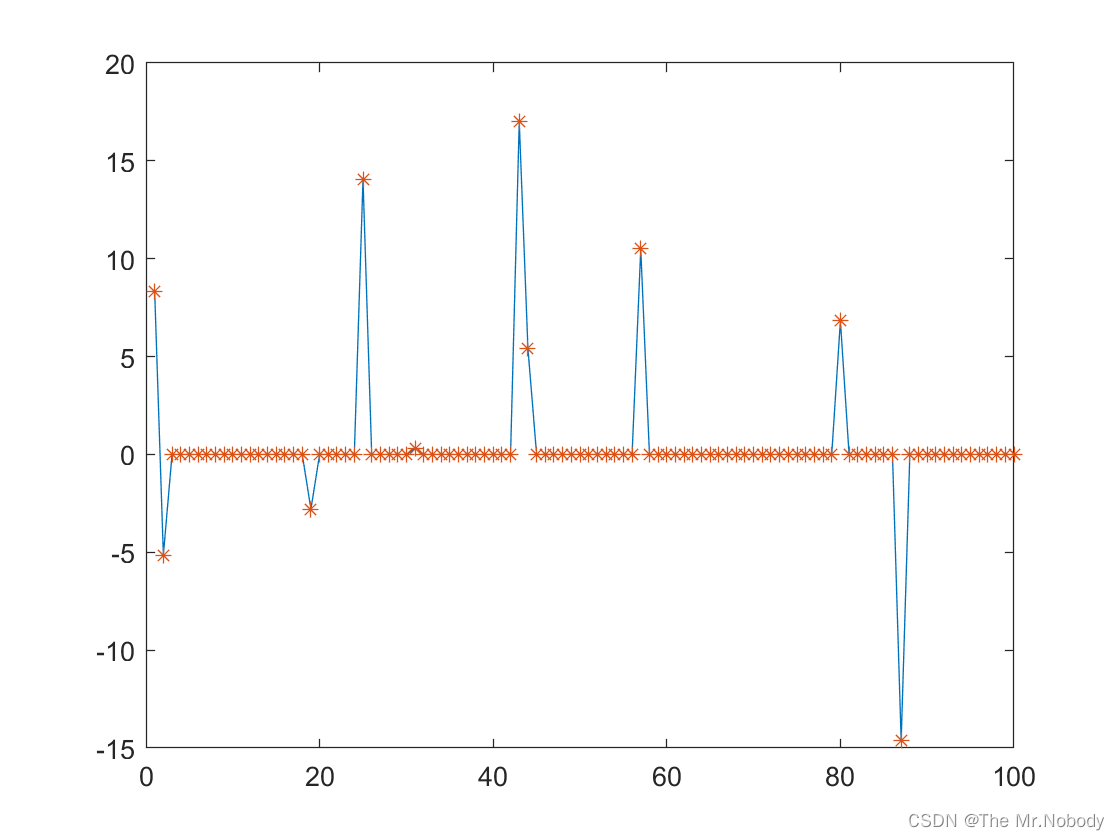
%% error analysis
plot(x);hold on
plot(x0,'*')

function x=CS_linprog(A,b)
    len=size(A,2);
    Phi=[A,-A];
    s=b;
    c=ones(1,2*len);
    lb=zeros(1,2*len);
    theta = linprog(c,[],[],Phi,s,lb);
    x=theta(1:len)-theta(len+1:2*len);
end