图的拓扑排序(AOV网络)

文章目录

- 拓扑排序
- - 概念
  - 实现
  - - 邻接表(队列)
    - 邻接矩阵(栈)
  - 总结
- 源代码
- - 邻接表
  - 邻接矩阵

拓扑排序

概念

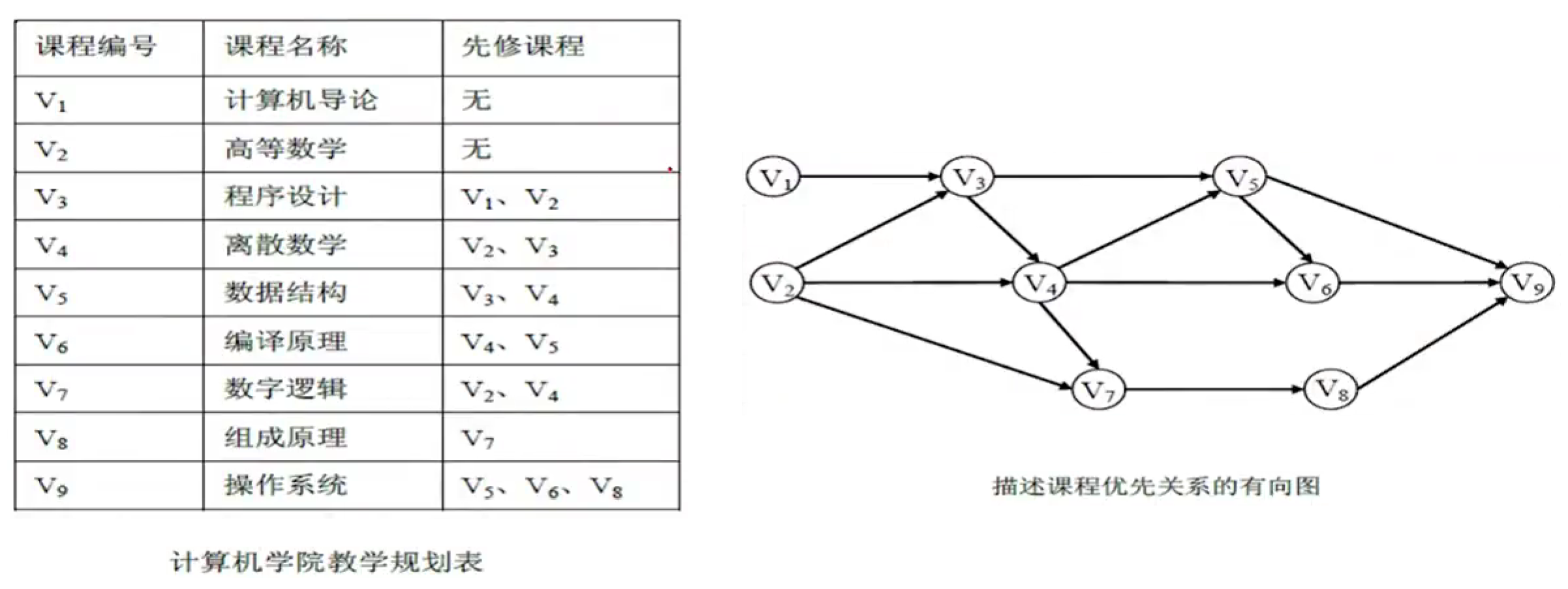
拓扑排序是对有向无环图的顶点的一种排序.

AOV网络 : 在有向图中, 用顶点表示活动或者任务, 弧表示活动或者任务间的优先关系, 则此有向图称为用顶点表示活动的网络(Activity On Vertex简称AOV网络).
拓扑序列(Topolagical Order) : 在有向无环图中, 若存在顶点v_i到顶点v_j的路径, 那么在序列中顶点v_i就排在顶点v_j的前面, 称此序列为拓扑排序.
拓扑排序(Topological Sort) : 将有向无环图的顶点按照它们之间的优先关系排成一个拓扑序列的操作称为拓扑排序.

拓扑排序可以解决先决条件问题, 即以某种线性顺序来组织多项任务, 使任务顺序完成.

拓扑序列应该满足 : 如果有向无环图G存在顶点v_i到v_j的一条路径, 那么在序列中顶点v_i必在顶点v_j之前.

实现

拓扑排序的步骤如下 :

在有向图中任选一个入度为0的顶点(即没有前驱的顶点)并输出它.
删除该顶点以及该顶点的所有出边, 将其邻接顶点的入度减一, 重复上述步骤, 最后结果可能有两种情况 : (1) 当输出了全部顶点时, 拓扑排序成功, 得到该图的拓扑排序. (2) 当图中还有顶点没有输出时, 拓扑排序失败, 说明该图中含有环, 剩余顶点的入度均不为零.

如何计算和存储顶点的入度?
定义一个整形数组inDegreeSize, 数组元素表示的各顶点的入度, 随图中边数的减少而减少. 从逻辑上删除某顶点以及该顶点的所有出边的操作, 可通过对该顶点的后继顶点的入度减一来实现. 此外, 为了便于查找入度为零的顶点, 可以另设一个存储空间来暂存入度为零的顶点 (可以用栈或者队列, 当度为零的顶点出栈或者出队时, 将对应的后继顶点的入度减一, 再将新的入度为零的顶点入栈或者入队) .

拓扑排序算法描述如下 :

计算每一个顶点的入度, 存入inDegreeSize数组, 遍历inDegreeSize数组并将所有入度为零的顶点入队列或者栈.
若队列或者栈非空, 从队头或者栈顶取出一个入度为零的顶点并输出它, 将以该顶点为弧尾的所有邻接顶点(弧头)的入度减一, 若此时某个邻接顶点的入度为零, 便将其入队或者入栈.
重复步骤2, 直到队列或者栈为空. 此时, 若所有顶点均被输出, 拓扑排序成功有意义返回true; 否则, 还有顶点未被输出表示图中有环, 拓扑排序失败没有意义返回false.

注意:在下面的邻接表与邻接矩阵中有写法一与写法二, 比较推荐编写写法一因为代价更低. 之所以有写法一与写法二只是想说明拓扑排序不唯一.

邻接表(队列)

namespace AdjacentList
{
	template<typename W>
	struct Edge
	{	
		int _dsti; // 终点顶点的下标
		W _weight; // 边的权值

		struct Edge<W>* _next; // 下一个结点的指针

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			,_weight(weight)
			,_next(nullptr)
		{}
	};

	template<typename V, typename W,bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度顶点表
    }
}

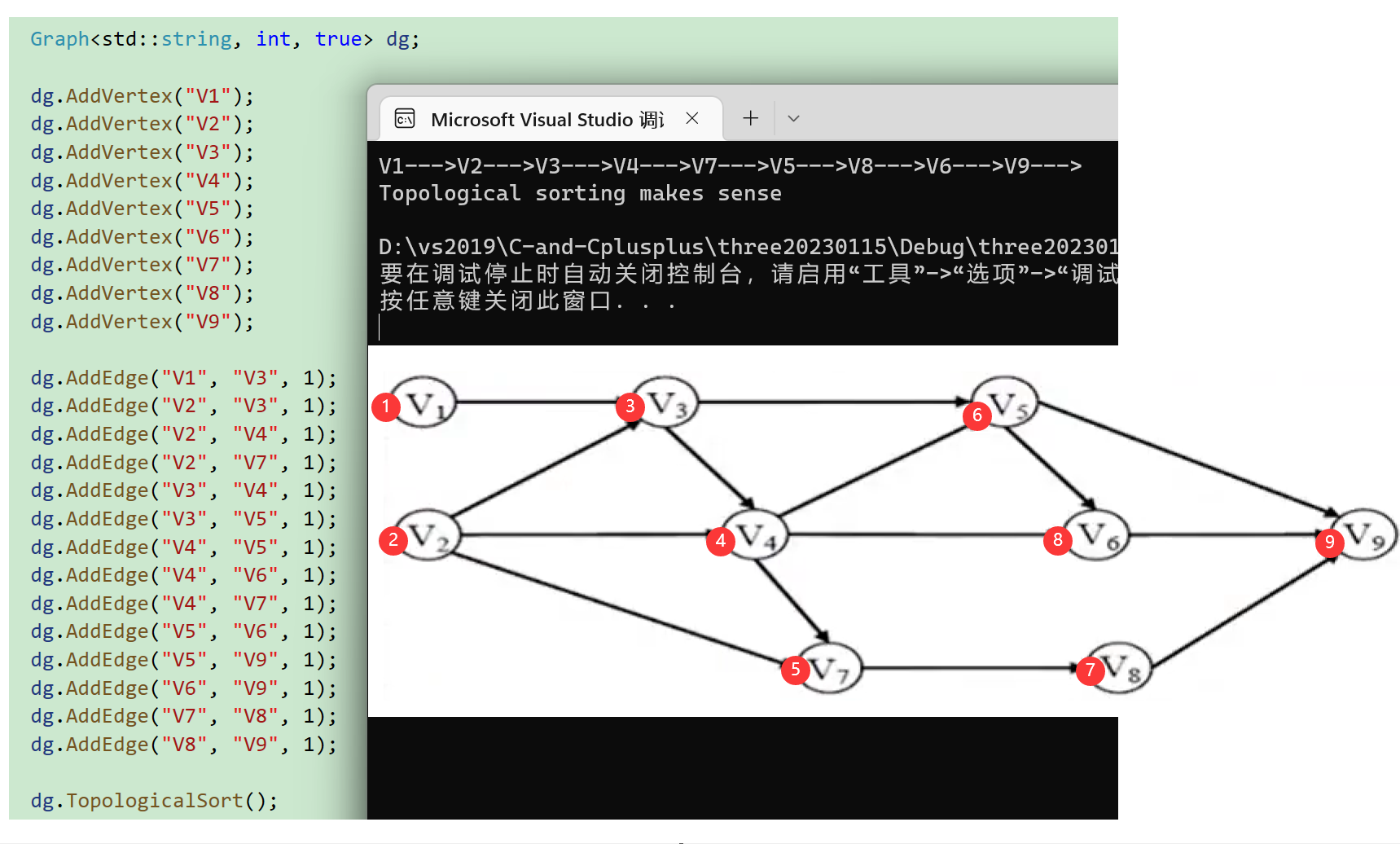
写法一:

	void TestGraph()
	{
        std::string aStr[] = {
			"V1","V2","V3","V4","V5","V6","V7","V8","V9"
		};
        
		Graph<std::string, int, true> dg(aStr,sizeof(aStr)/sizeof(aStr[0]));
        
		dg.AddEdge("V1", "V3", 1);
		dg.AddEdge("V2", "V3", 1);
		dg.AddEdge("V2", "V4", 1);
		dg.AddEdge("V2", "V7", 1);
		dg.AddEdge("V3", "V4", 1);
		dg.AddEdge("V3", "V5", 1);
		dg.AddEdge("V4", "V5", 1);
		dg.AddEdge("V4", "V6", 1);
		dg.AddEdge("V4", "V7", 1);
		dg.AddEdge("V5", "V6", 1);
		dg.AddEdge("V5", "V9", 1);
		dg.AddEdge("V6", "V9", 1);
		dg.AddEdge("V7", "V8", 1);
		dg.AddEdge("V8", "V9", 1);

		dg.TopologicalSort();
	}

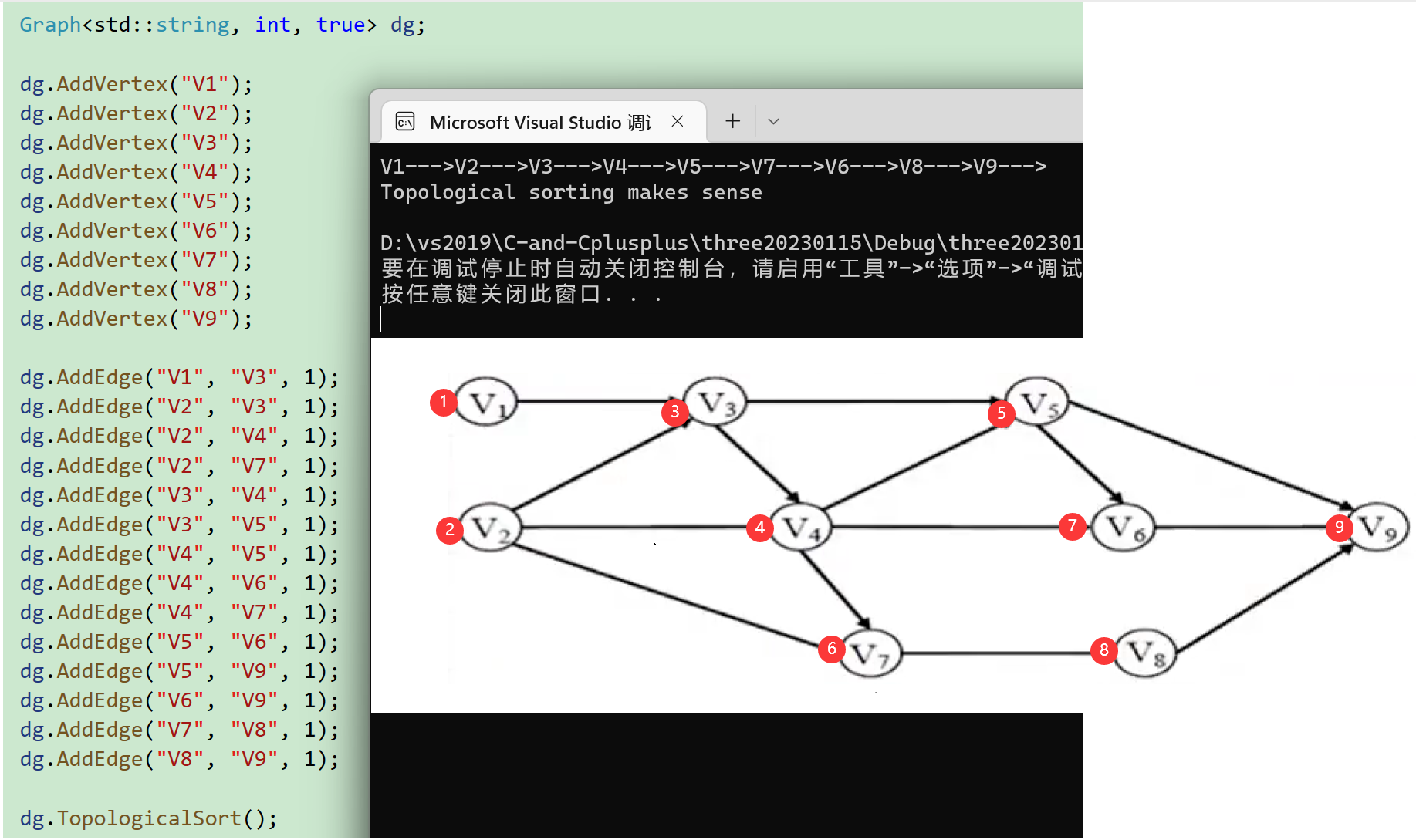
写法二:

邻接矩阵(栈)

namespace AdjacentMatrix
{
	template<class V,class W=int,W W_MAX=INT_MAX,bool Directed=false>
	class Graph
	{
	private:
		std::vector<V> _vertexs; // 顶点集合，下标找顶点

		std::vector<vector<W>> _matrix; // 邻接矩阵，顶点与顶点之间的权值

		YX::RedBlackTree<V, int> _findIndexTree; // 顶点与下标的映射，顶点找下标
    }
}

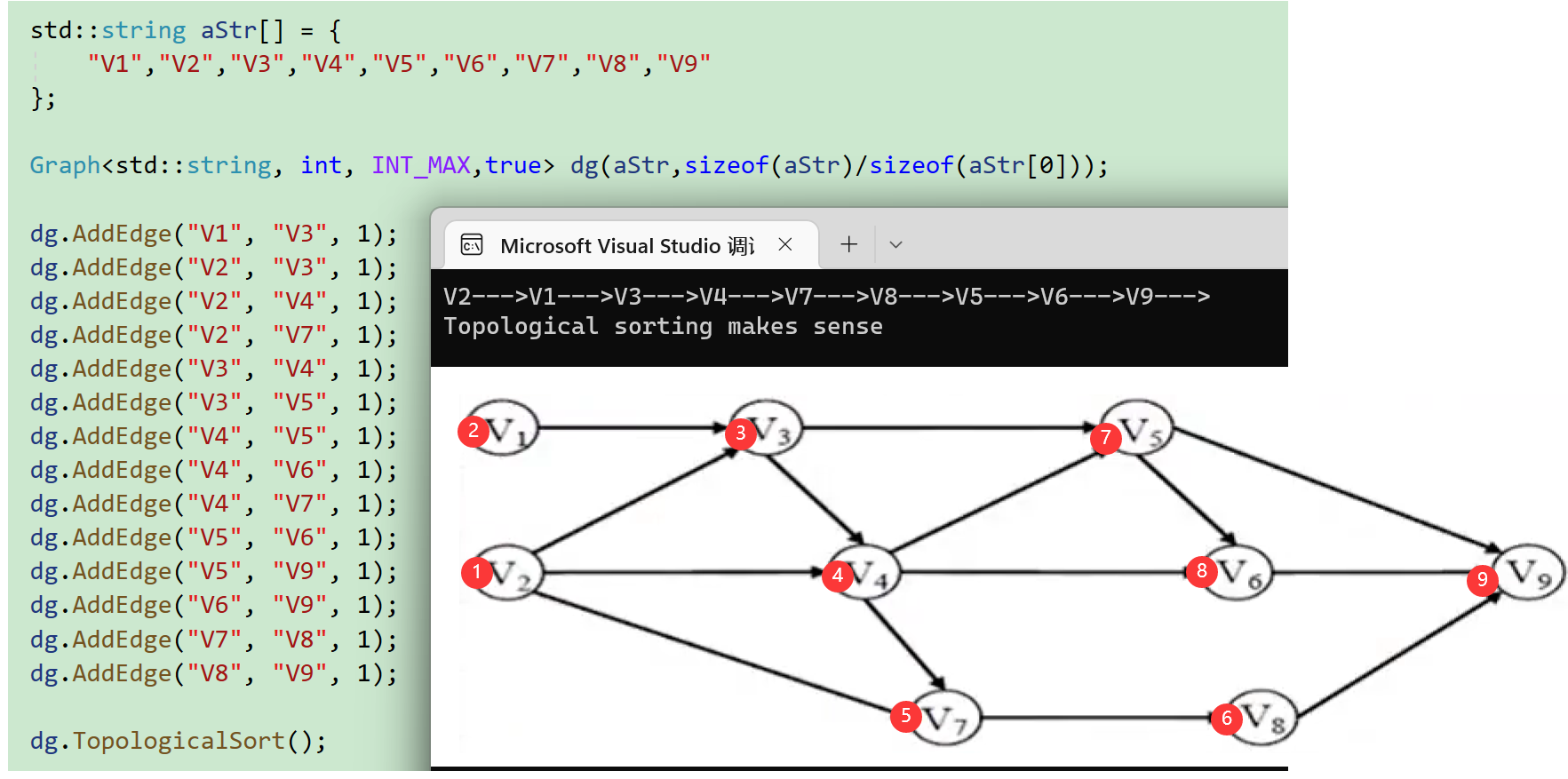
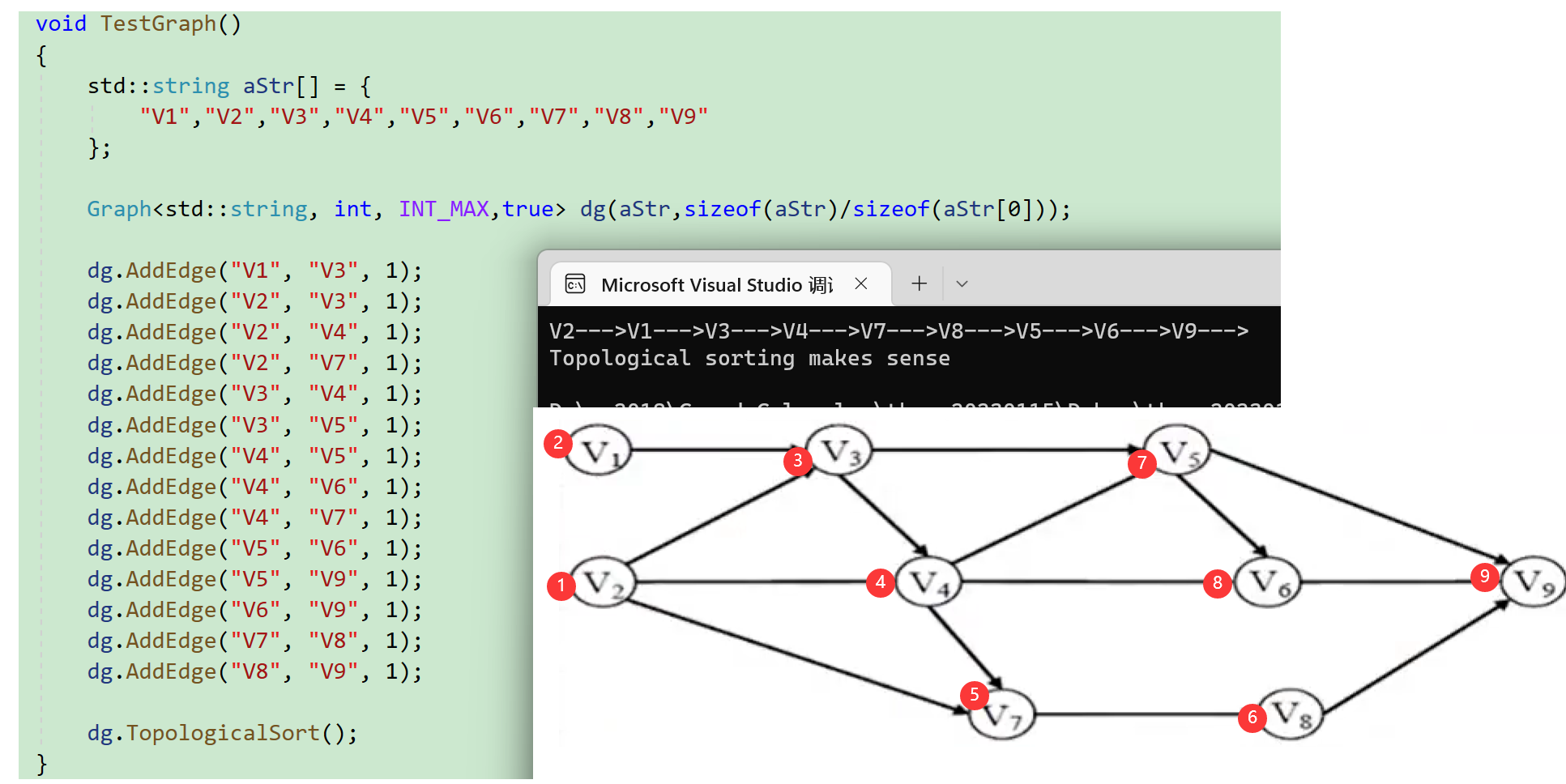
写法一:

	void TestGraph()
	{
		std::string aStr[] = {
			"V1","V2","V3","V4","V5","V6","V7","V8","V9"
		};

		Graph<std::string, int, INT_MAX,true> dg(aStr,sizeof(aStr)/sizeof(aStr[0]));
		
		dg.AddEdge("V1", "V3", 1);
		dg.AddEdge("V2", "V3", 1);
		dg.AddEdge("V2", "V4", 1);
		dg.AddEdge("V2", "V7", 1);
		dg.AddEdge("V3", "V4", 1);
		dg.AddEdge("V3", "V5", 1);
		dg.AddEdge("V4", "V5", 1);
		dg.AddEdge("V4", "V6", 1);
		dg.AddEdge("V4", "V7", 1);
		dg.AddEdge("V5", "V6", 1);
		dg.AddEdge("V5", "V9", 1);
		dg.AddEdge("V6", "V9", 1);
		dg.AddEdge("V7", "V8", 1);
		dg.AddEdge("V8", "V9", 1);

		dg.TopologicalSort();
	}

写法二:

总结

与图的遍历相同:

图的每条边弧处理一次
图的每个顶点访问一次

采用邻接表表示时, 时间复杂度为O(n+e).

采用邻接矩阵表示时, 时间复杂度O(n²).

空间复杂度都为O(n).

源代码

邻接表

namespace AdjacentList
{
	template<typename W>
	struct Edge
	{
		int _dsti;
		W _weight;

		struct Edge<W>* _next;

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			, _weight(weight)
			, _next(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度边表
	public:

		typedef Graph<V, W, Directed> Self;

		Graph() = default;

		Graph(const V* a, int n)
		{
			for (int i = 0; i < n; i++)
			{
				AddVertex(a[i]);
			}
		}

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);

			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			_table.push_back(nullptr);

			return true;
		}

		bool _AddEdge(int srci, int dsti, const W& weight)
		{
			Edge* edge = new Edge(dsti, weight);

			// 头插
			edge->_next = _table[srci];
			_table[srci] = edge;

			// 无向图
			if (!Directed)
			{
				edge = new Edge(srci, weight);

				edge->_next = _table[dsti];
				_table[dsti] = edge;
			}

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			//Edge* edge = new Edge(dsti, weight);

			 头插
			//edge->_next = _table[srci];
			//_table[srci] = edge;

			 无向图
			//if (!Directed)
			//{
			//	edge = new Edge(srci, weight);

			//	edge->_next = _table[dsti];
			//	_table[dsti] = edge;
			//}

			return _AddEdge(srci, dsti, weight);
		}

		//bool TopologicalSort()
		//{
		//	if (!Directed)
		//		return false;

		//	// 记录顶点的入度大小
		//	std::vector<int> inDegreeSize(_vertexSet.size(), 0);
		//	// 记录顶点是否被访问过(即是否入过队或者栈)
		//	std::vector<bool> visited(_vertexSet.size(), false);

		//	// 顶点个数
		//	int n = static_cast<int>(_vertexSet.size());

		//	// 获取图中所有顶点对应的入度大小
		//	for (int i = 0; i < n; i++)
		//	{
		//		Edge* curr = _table[i];

		//		while (curr != nullptr)
		//		{	
		//			inDegreeSize[curr->_dsti]++;
		//			curr = curr->_next;
		//		}
		//	}
		//	
		//	// 记录入度为零的顶点
		//	std::queue<int> q;

		//	// 将入度为零的顶点下标入队或者入栈
		//	for (int i = 0; i < n; i++)
		//	{
		//		if (inDegreeSize[i] == 0 && !visited[i])
		//		{
		//			q.push(i);
		//			visited[i] = true;
		//		}
		//	}

		//	while (!q.empty())
		//	{
		//		// 先遍历某入度为零的顶点
		//		int front = q.front();
		//		q.pop();
		//		std::cout << _vertexSet[front] << "--->";// << std::endl;

		//		// 再将该顶点对应的后继顶点的入度减一
		//		Edge* curr = _table[front];

		//		while (curr != nullptr)
		//		{
		//			inDegreeSize[curr->_dsti]--;

		//			curr = curr->_next;
		//		}

		//		// 最后将没有入过队或者栈的入度为零的顶点入队
		//		for (int i = 0; i < n; i++)
		//		{
		//			if (inDegreeSize[i] == 0 && !visited[i])
		//			{
		//				q.push(i);
		//				visited[i] = true;
		//			}
		//		}
		//	}

		//	// 判断是否还有顶点没有访问到
		//	for (int i = 0; i < n; i++)
		//	{
		//		if (inDegreeSize[i] != 0 && !visited[i])
		//		{
		//			printf("\nTopological sorting doesn't make sense\n");
		//			return false;
		//		}
		//	}

		//	printf("\nTopological sorting makes sense\n");
		//	return true;
		//}
		
		bool TopologicalSort()
		{
			if (!Directed)
				return false;

			// 记录顶点的入度大小
			std::vector<int> inDegreeSize(_vertexSet.size(), 0);

			// 顶点个数
			int n = static_cast<int>(_vertexSet.size());

			// 获取图中所有顶点对应的入度大小
			for (int i = 0; i < n; i++)
			{
				Edge* curr = _table[i];

				while (curr != nullptr)
				{
					inDegreeSize[curr->_dsti]++;
					curr = curr->_next;
				}
			}

			// 记录入度为零的顶点
			std::queue<int> q;

			// 将入度为零的顶点下标入队或者入栈
			for (int i = 0; i < n; i++)
			{
				if (inDegreeSize[i] == 0)
				{
					q.push(i);
				}
			}

			while (!q.empty())
			{
				// 先遍历某入度为零的顶点
				int front = q.front();
				q.pop();
				std::cout << _vertexSet[front] << "--->";// << std::endl;

				// 再将该顶点对应的后继顶点的入度减一
				Edge* curr = _table[front];

				while (curr != nullptr)
				{
					// 如果有顶点的入度被减为零时,则该顶点入队或者入栈
					if (--inDegreeSize[curr->_dsti] == 0)
					{
						q.push(curr->_dsti);
					}
					curr = curr->_next;
				}
			}

			// 判断是否还有顶点没有访问到
			for (int i = 0; i < n; i++)
			{
				if (inDegreeSize[i] != 0)
				{
					printf("\nTopological sorting doesn't make sense\n");
					return false;
				}
			}

			printf("\nTopological sorting makes sense\n");
			return true;
		}
	};

	void TestGraph()
	{
		Graph<std::string, int, true> dg;

		dg.AddVertex("V1");
		dg.AddVertex("V2");
		dg.AddVertex("V3");
		dg.AddVertex("V4");
		dg.AddVertex("V5");
		dg.AddVertex("V6");
		dg.AddVertex("V7");
		dg.AddVertex("V8");
		dg.AddVertex("V9");

		dg.AddEdge("V1", "V3", 1);
		dg.AddEdge("V2", "V3", 1);
		dg.AddEdge("V2", "V4", 1);
		dg.AddEdge("V2", "V7", 1);
		dg.AddEdge("V3", "V4", 1);
		dg.AddEdge("V3", "V5", 1);
		dg.AddEdge("V4", "V5", 1);
		dg.AddEdge("V4", "V6", 1);
		dg.AddEdge("V4", "V7", 1);
		dg.AddEdge("V5", "V6", 1);
		dg.AddEdge("V5", "V9", 1);
		dg.AddEdge("V6", "V9", 1);
		dg.AddEdge("V7", "V8", 1);
		dg.AddEdge("V8", "V9", 1);

		dg.TopologicalSort();
	}
}

邻接矩阵

namespace AdjacentMatrix
{
	template<typename V, typename W, W W_MAX, bool Directed = false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
	public:

		typedef Graph<V, W, W_MAX, Directed> Self;

		Graph() = default;

		Graph(const V* a, int n)
		{
			for (int i = 0; i < n; i++)
			{
				AddVertex(a[i]);
			}
		}

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			// 顶点存在不需要继续增加
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);
			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			// 先在原有的行上一列
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].push_back(W_MAX);
			}

			// 增加一行
			_matrix.push_back(std::vector<W>(_vertexSet.size(), W_MAX));

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			//_matrix[srci][dsti] = weight;

			 如果为无向图,则需要再添加一条dst->src的边
			//if (!Directed)
			//{
			//	_matrix[dsti][srci] = weight;
			//}

			//return true;

			return _AddEdge(srci, dsti, weight);
		}

		bool _AddEdge(int srci, int dsti, const W& weight)
		{
			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			_matrix[srci][dsti] = weight;

			// 如果为无向图,则需要再添加一条dst->src的边
			if (!Directed)
			{
				_matrix[dsti][srci] = weight;
			}

			return true;
		}

		//bool TopologicalSort()
		//{
		//	if (!Directed)
		//		return false;

		//	// 记录顶点的入度大小
		//	std::vector<int> inDegreeSize(_vertexSet.size(), 0);
		//	// 记录顶点是否被访问过(即是否入过队或者栈)
		//	std::vector<bool> visited(_vertexSet.size(), false);

		//	// 顶点个数
		//	int n = static_cast<int>(_vertexSet.size());
		//	
		//	// 统计图中所有顶点的入度数
		//	for (int i = 0; i < n; i++)
		//	{
		//		for (int j = 0; j < n; j++)
		//		{
		//			if (_matrix[i][j] != W_MAX)
		//			{
		//				inDegreeSize[j]++;
		//			}
		//		}
		//	}

		//	// 将入度为零的顶点压入栈中
		//	std::stack<int> st;
		//	for (int i = 0; i < n; i++)
		//	{
		//		if (inDegreeSize[i] == 0 && !visited[i])
		//		{
		//			st.push(i);
		//			visited[i] = true;
		//		}
		//	}
		//	// 栈不为空时,将存储在栈中入度为零的顶点输出
		//	while (!st.empty())
		//	{
		//		int top = st.top();
		//		st.pop();
		//		// 输出栈顶元素
		//		std::cout << _vertexSet[top] << "--->";

		//		// 将以该顶点为弧尾的边对应顶点的入度减一
		//		for (int i = 0; i < n; i++)
		//		{
		//			if (top != i && _matrix[top][i] != W_MAX)
		//			{
		//				inDegreeSize[i]--;
		//			}
		//		}

		//		// 最后将没有入栈的入度为零的顶点入栈
		//		for (int i = 0; i < n; i++)
		//		{
		//			if (inDegreeSize[i] == 0 && !visited[i])
		//			{
		//				st.push(i);
		//				visited[i] = true;
		//			}
		//		}
		//	}

		//	// 判断是否还有顶点没有访问到
		//	for (int i = 0; i < n; i++)
		//	{
		//		if (inDegreeSize[i] != 0 && !visited[i])
		//		{
		//			printf("\nTopological sorting doesn't make sense\n");
		//			return false;
		//		}
		//	}

		//	printf("\nTopological sorting makes sense\n");
		//	return true;
		//}

		bool TopologicalSort()
		{
			if (!Directed)
				return false;

			// 记录顶点的入度大小
			std::vector<int> inDegreeSize(_vertexSet.size(), 0);
			// 顶点个数
			int n = static_cast<int>(_vertexSet.size());

			// 统计图中所有顶点的入度数
			for (int i = 0; i < n; i++)
			{
				for (int j = 0; j < n; j++)
				{
					if (_matrix[i][j] != W_MAX)
					{
						inDegreeSize[j]++;
					}
				}
			}

			// 将入度为零的顶点压入栈中
			std::stack<int> st;
			for (int i = 0; i < n; i++)
			{
				if (inDegreeSize[i] == 0)
				{
					st.push(i);
				}
			}
			// 栈不为空时,将存储在栈中入度为零的顶点输出
			while (!st.empty())
			{
				int top = st.top();
				st.pop();
				// 输出栈顶元素
				std::cout << _vertexSet[top] << "--->";

				// 将以该顶点为弧尾的边对应顶点的入度减一
				for (int i = 0; i < n; i++)
				{
					if (top != i && _matrix[top][i] != W_MAX)
					{
						// 如果有顶点的入度被减为零时,则该顶点入队或者入栈
						if (--inDegreeSize[i] == 0)
						{
							st.push(i);
						}
					}
				}
			}

			// 判断是否还有顶点没有访问到
			for (int i = 0; i < n; i++)
			{
				if (inDegreeSize[i] != 0)
				{
					printf("\nTopological sorting doesn't make sense\n");
					return false;
				}
			}

			printf("\nTopological sorting makes sense\n");
			return true;
		}
	};

	void TestGraph()
	{
		std::string aStr[] = {
			"V1","V2","V3","V4","V5","V6","V7","V8","V9"
		};

		Graph<std::string, int, INT_MAX,true> dg(aStr,sizeof(aStr)/sizeof(aStr[0]));
		
		dg.AddEdge("V1", "V3", 1);
		dg.AddEdge("V2", "V3", 1);
		dg.AddEdge("V2", "V4", 1);
		dg.AddEdge("V2", "V7", 1);
		dg.AddEdge("V3", "V4", 1);
		dg.AddEdge("V3", "V5", 1);
		dg.AddEdge("V4", "V5", 1);
		dg.AddEdge("V4", "V6", 1);
		dg.AddEdge("V4", "V7", 1);
		dg.AddEdge("V5", "V6", 1);
		dg.AddEdge("V5", "V9", 1);
		dg.AddEdge("V6", "V9", 1);
		dg.AddEdge("V7", "V8", 1);
		dg.AddEdge("V8", "V9", 1);

		dg.TopologicalSort();
	}
}