0. 前言

图卷积网络 (Graph Convolutional Network, GCN) 架构由 Kipf 和 Welling 于 2017 年提出，其理念是创建一种适用于图的高效卷积神经网络 (Convolutional Neural Networks, CNN)。更准确地说，它是图信号处理中图卷积操作的近似，由于其易用性，GCN 已成为最受欢迎的图神经网络 (Graph Neural Networks, GNN) 之一，是处理图数据时创建基线模型的首选架构。
在本节中，我们将讨论 Vanilla GNN 架构的局限性，这有助于我们理解 GCN 的核心思想。并详细介绍 GCN 的工作原理，解释为什么 GCN 比 Vanilla GNN 性能更好，通过使用 PyTorch Geometric 在 Cora 和 Facebook Page-Page 数据集上实现 GCN 来验证其性能。

1. 图卷积层

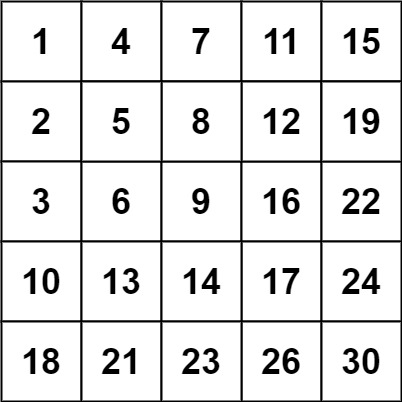
与表格或图像数据不同，图数据中节点的邻居数量并不总是相同。例如，在下图中，节点 1 有 3 个邻居，而节点 2 只有 1 个：

但是，观察图神经网络 (Graph Neural Networks, GNN) 层就会发现，邻居数量的差异并不会导致计算的复杂化。GNN 层由一个简单的求和公式组成，没有任何归一化系数，计算节点 $i$ 的嵌入方法如下：
$$h_i=\sum _{j\in {\mathcal{N}}_i}{x}_j{W}^T$$
假设节点 1 有 1,000 个邻居，而节点 2 只有 1 个邻居，那么 $h_1$ 嵌入的值将远远大于 $h_2$ 嵌入的值。这样便会出现一个问题，当我们要对这些嵌入进行比较时，如果它们的值相差过大，如何进行有意义的比较？
一个简单的解决方案是将嵌入除以邻居数量，用 $\mathrm{deg}(A)$ 表示节点的度，因此 GNN 层公式可以更新为：
$$h_i=\frac{1}{\mathrm{deg}(i)}\sum _{j\in {\mathcal{N}}_i}{x}_j{W}^T$$
那么如何将其转化为矩阵乘法呢？首先回顾普通 GNN 层的计算公式：
$$H={\tilde{A}}^{T}X{W}^T$$
其中，$\tilde{A}=A+I$。公式中缺少的是一个能为我们提供归一化系数 $\frac{1}{\mathrm{deg}(A)}$ 的矩阵，可以利用度矩阵 $D$ 来计算每个节点的邻居数量。上示图像中的图的度矩阵如下：
$$D=\left[\begin{array}{cccc}3& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 2\end{array}\right]$$
使用 NumPy 表示以上矩阵：

import numpy as np

D = np.array([
    [3, 0, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 2, 0],
    [0, 0, 0, 2]
])

根据定义，$D$ 给出了每个节点的度 $\mathrm{deg}(i)$ 。因此，根据度矩阵的逆矩阵 $D^{-1}$ 可以直接得到归一化系数 $\frac{1}{\mathrm{deg}(A)}$：

可以使用 numpy.linalg.inv() 函数计算矩阵的逆：

print(np.linalg.inv(D))
'''输出如下
[[0.33333333 0.         0.         0.        ]
 [0.         1.         0.         0.        ]
 [0.         0.         0.5        0.        ]
 [0.         0.         0.         0.5       ]]
'''

为了更加精确，在图中添加了自循环，用 $\tilde{A}=A+I$ 表示。同样，我们也需要在度矩阵中加入自循环，即 $\tilde{D}=D+I$ ，因此最终所需的矩阵为 ${\tilde{D}}^{-1}=(D+I{)}^{-1}$：

在 NumPy 中，可以使用函数 numpy.identity(n) 快速创建指定维度 n 的单位矩阵 $I$：

print(np.linalg.inv(D + np.identity(4)))
'''输出如下
[[0.25       0.         0.         0.        ]
 [0.         0.5        0.         0.        ]
 [0.         0.         0.33333333 0.        ]
 [0.         0.         0.         0.33333333]]
'''

得到归一化系数矩阵后，有两种应用方式：

• ${\tilde{D}}^{-1}\tilde{A}X{W}^T$ 会对每一行特征进行归一化处理。
• $\tilde{A}{\tilde{D}}^{-1}X{W}^T$ 会对每一列特征进行归一化处理。

接下来，通过计算 ${\tilde{D}}^{-1}\tilde{A}$ 和 $\tilde{A}{\tilde{D}}^{-1}$ 进行验证：

$$\begin{gathered} {\tilde{D}}^{-1}\tilde{A}=\left[\begin{array}{cccc}\frac{1}{4}& 0& 0& 0\\ 0& \frac{1}{2}& 0& 0\\ 0& 0& \frac{1}{3}& 0\\ 0& 0& 0& \frac{1}{3}\end{array}\right]\cdot \left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& 0& 0\\ 1& 0& 1& 1\\ 1& 0& 1& 1\end{array}\right]=\left[\begin{array}{cccc}\frac{1}{4}& \frac{1}{4}& \frac{1}{4}& \frac{1}{4}\\ \frac{1}{2}& \frac{1}{2}& 0& 0\\ \frac{1}{3}& 0& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& 0& \frac{1}{3}& \frac{1}{3}\end{array}\right] \\ \tilde{A}{\tilde{D}}^{-1}=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& 0& 0\\ 1& 0& 1& 1\\ 1& 0& 1& 1\end{array}\right]\cdot \left[\begin{array}{cccc}\frac{1}{4}& 0& 0& 0\\ 0& \frac{1}{2}& 0& 0\\ 0& 0& \frac{1}{3}& 0\\ 0& 0& 0& \frac{1}{3}\end{array}\right]=\left[\begin{array}{cccc}\frac{1}{4}& \frac{1}{2}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{4}& \frac{1}{2}& 0& 0\\ \frac{1}{4}& 0& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{4}& 0& \frac{1}{3}& \frac{1}{3}\end{array}\right] \end{gathered}$$

在第一种情况下，每一行的和都等于 1；在第二种情况下，每一列的和都等于 1。矩阵乘法可以使用 numpy.matmul() 函数执行，或使用 Python 内置的矩阵乘法运算符 @。定义邻接矩阵并使用 @ 操作符计算矩阵乘法：

A = np.array([
    [1, 1, 1, 1],
    [1, 1, 0, 0],
    [1, 0, 1, 1],
    [1, 0, 1, 1]
])
print(np.linalg.inv(D + np.identity(4)) @ A)
print('------------------------------')
print(A @ np.linalg.inv(D + np.identity(4)))
'''输出如下
[[0.25       0.25       0.25       0.25      ]
 [0.5        0.5        0.         0.        ]
 [0.33333333 0.         0.33333333 0.33333333]
 [0.33333333 0.         0.33333333 0.33333333]]
------------------------------
[[0.25       0.5        0.33333333 0.33333333]
 [0.25       0.5        0.         0.        ]
 [0.25       0.         0.33333333 0.33333333]
 [0.25       0.         0.33333333 0.33333333]]
'''

得到的结果与手动计算的矩阵乘法相同。那么，在实践中我们应该使用哪种应用方式？第一种方案似乎看起来合理，因为它能很好地对相邻节点特征进行归一化处理。
但 Kipf 和 Welling 提出，具有多个邻居的节点的特征很容易传播，而与之相反，孤立节点的特征不容易传播。在 GCN 论文中，作者提出了一种混合归一化方法来平衡这种影响。在实践中，使用以下公式为邻居较少的节点分配更高的权重：
$$H={\tilde{D}}^{-\frac{1}{2}}{\tilde{A}}^T{\tilde{D}}^{-\frac{1}{2}}X{W}^T$$
就单个嵌入而言，上式可以写为：
$$h_i=\sum _{j\in {\mathcal{N}}_i}\frac{1}{\sqrt{\mathrm{deg}(i)}\sqrt{\mathrm{deg}(j)}}{x}_j{W}^T$$
这就是实现原始图卷积层的数学公式。与普通的 GNN 层一样，我们可以通过堆叠图卷积层创建 GCN。接下来，使用 PyTorch Geometric 实现一个 GCN 模型，并验证其性能是否优于原始图神经网络模型。

2. 比较 GCN 和 GNN

我们已经证明了 vanilla GNN 性能优于 Node2Vec 模型，接下来，我们将其与 GCN 进行比较，比较它们在 Cora 和 Facebook Page-Page 数据集上的表现。
与普通 GNN 相比，GCN 的主要特点是通过考虑节点度来权衡其特征。在构建模型之前，我们首先计算这两个数据集中的节点度，这与 GCN 的性能直接相关。
根据我们对 GCN 架构的了解，可以猜测当节点度差异较大时，它的性能会更好。如果每个节点都有相同数量的邻居，那么无论使用哪种归一化方式，架构之间都是等价的：$\sqrt{\mathrm{deg}(i)}\sqrt{\mathrm{deg}(i)}=\mathrm{deg}(i)$。

2.1 数据集分析

(1) 从 PyTorch Geometric 中导入 Planetoid 类，为了可视化节点度，同时导入两个附加类( degree 用于获取每个节点的邻居数，Counter 用于计算每个度数的节点数)和 matplotlib 库：

import torch
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import degree
from collections import Counter
import matplotlib.pyplot as plt

(2) 导入 Cora 数据集，并将图存储在 data 中：

dataset = Planetoid(root=".", name="Cora")
data = dataset[0]

(3) 计算图中每个节点的邻居数：

degrees = degree(data.edge_index[0]).numpy()

(4) 为了生成更自然的可视化效果，统计具有相同度的节点数量：

numbers = Counter(degrees)

(5) 使用条形图来绘制统计结果：

fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()

从上图中可以看出，图中的度分布近似指数分布，从 1 个邻居( 485 个节点)到 168 个邻居( 1 个节点)不等，这种不平衡的数据集正是归一化处理的用武之地。

(6) 在 Facebook Page-Page 数据集上重复同样的过程：

from torch_geometric.datasets import FacebookPagePage

# Import dataset from PyTorch Geometric
dataset = FacebookPagePage(root=".")
data = dataset[0]

# Create masks
data.train_mask = range(18000)
data.val_mask = range(18001, 20000)
data.test_mask = range(20001, 22470)

# Get list of degrees for each node
degrees = degree(data.edge_index[0]).numpy()

# Count the number of nodes for each degree
numbers = Counter(degrees)

# Bar plot
fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()

Facebook Page-Page 数据集的图的节点度分布看起来更加失衡，邻居数量从 1 到 709 不等。出于同样的原因，Facebook Page-Page 数据集也是应用 GCN 的合适实例。

2.2 实现 GCN 架构

我们可以从零开始实现 GCN 层，但这里我们无需再从头造轮子，PyTorch Geometric 已经内置了 GCN 层，首先在 Cora 数据集上实现 GCN 架构。

(1) 从 PyTorch Geometric 中导入 GCN 层，并导入 PyTorch：

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv

dataset = Planetoid(root=".", name="Cora")
data = dataset[0]

(2) 创建函数 accuracy() 计算模型准确率：

def accuracy(y_pred, y_true):
    """Calculate accuracy."""
    return torch.sum(y_pred == y_true) / len(y_true)

(3) 创建 GCN 类，其中 __init__() 函数接受三个参数作为输入：输入维度 dim_in、隐藏维度 dim_h 和输出维度 dim_out：

class GCN(torch.nn.Module):
    """Graph Convolutional Network"""
    def __init__(self, dim_in, dim_h, dim_out):
        super().__init__()
        self.gcn1 = GCNConv(dim_in, dim_h)
        self.gcn2 = GCNConv(dim_h, dim_out)

(4) forward() 方法使用两个 GCN 层，并对分类结果应用 log_softmax 函数：

    def forward(self, x, edge_index):
        h = self.gcn1(x, edge_index)
        h = torch.relu(h)
        h = self.gcn2(h, edge_index)
        return F.log_softmax(h, dim=1)

(5) fit() 方法与 Vanilla GNN 相同，为了更好的比较，使用具有相同参数的 Adam 优化器，其中学习率 lr 为 0.1，L2 正则化 weight_decay 为 0.0005：

    def fit(self, data, epochs):
        criterion = torch.nn.CrossEntropyLoss()
        optimizer = torch.optim.Adam(self.parameters(),
                                      lr=0.01,
                                      weight_decay=5e-4)

        self.train()
        for epoch in range(epochs+1):
            optimizer.zero_grad()
            out = self(data.x, data.edge_index)
            loss = criterion(out[data.train_mask], data.y[data.train_mask])
            acc = accuracy(out[data.train_mask].argmax(dim=1),
                          data.y[data.train_mask])
            loss.backward()
            optimizer.step()

            if(epoch % 20 == 0):
                val_loss = criterion(out[data.val_mask], data.y[data.val_mask])
                val_acc = accuracy(out[data.val_mask].argmax(dim=1),
                                  data.y[data.val_mask])
                print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | Train Acc:'
                      f' {acc*100:>5.2f}% | Val Loss: {val_loss:.2f} | '
                      f'Val Acc: {val_acc*100:.2f}%')

(6) 编写 test() 方法：

    @torch.no_grad()
    def test(self, data):
        self.eval()
        out = self(data.x, data.edge_index)
        acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
        return acc

(7) 实例化模型并训练 100 个 epoch：

# Create the Vanilla GNN model
gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)

# Train
gcn.fit(data, epochs=100)

训练过程中的输出结果如下：

(8) 最后，在测试集上对模型进行评估：

acc = gcn.test(data)
print(f'\nGCN test accuracy: {acc*100:.2f}%\n')

# GCN test accuracy: 80.30%

重复此实验 100 次，模型的平均准确率为 80.26%(±0.59%)，明显 vanilla GNN 模型的平均准确率 74.99%(±1.60%)。

(9) 将同样的模型应用于 Facebook Page-Page 数据集，其平均准确率可以达到 91.78%(±0.31%)，同样比 vanilla GNN 的结果( 84.91%(±1.88%) )高出很多：

# Load Facebook Page-Page
dataset = FacebookPagePage(root=".")
data = dataset[0]
data.train_mask = range(18000)
data.val_mask = range(18001, 20000)
data.test_mask = range(20001, 22470)

# Train GCN
gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)
gcn.fit(data, epochs=100)
acc = gcn.test(data)
print(f'\nGCN test accuracy: {acc*100:.2f}%\n')

下表总结了不同模型在不同数据集上的准确率和标准差：

	MLP	GNN	GCN
Cora	53.47%(±1.95%)	74.99%(±1.60%)	80.26%(±0.59%)
Facebook	75.22%(±0.39%)	84.91%(±1.88%)	91.78%(±0.31%)

我们可以将这些性能提升归因于这两个数据集中节点度的分布的不平衡性。通过对特征进行归一化处理，并考虑中心节点及其邻居的数量，GCN 的灵活性得到了极大的提升，可以很好地处理各种类型的图。但节点分类远不是 GCN 的唯一应用，在之后的学习中，我们将看到 GCN 模型的更多新颖应用。

小结

在本节中，我们改进了 vanilla GNN 层，使其能够正确归一化节点特征，这一改进引入了图卷积网络 (Graph Convolutional Network, GCN) 层和混合归一化。在 Cora 和 Facebook Page-Page 数据集上，我们对比了 GCN 架构与 Node2Vec 和 vanilla GNN 之间的性能差异。由于采用了归一化处理，GCN 在这两个数据集中都具有较高的准确率。

系列链接

图神经网络实战（1）——图神经网络(Graph Neural Networks, GNN)基础
图神经网络实战（2）——图论基础
图神经网络实战（3）——基于DeepWalk创建节点表示
图神经网络实战（4）——基于Node2Vec改进嵌入质量
图神经网络实战（5）——常用图数据集
图神经网络实战（6）——使用PyTorch构建图神经网络