NumPy（Numerical Python）是一个开源的Python库，广泛用于科学计算。它提供了一个高性能的多维数组对象，以及用于处理这些数组的工具和函数。NumPy是数据分析、机器学习、工程和科学研究中不可或缺的工具之一，因为它提供了简单而高效的数值运算功能。

1.NumPy的主要功能：

1. 高效的数组运算：NumPy的数组比Python的内置数据结构更加高效和快速。

2. 广播功能：能够处理不同大小数组之间的运算。

3. 数学函数：包含大量的数学函数，用于在数组上执行各种数学运算。

4. 线性代数、傅里叶变换和随机数生成：提供了丰富的库和API支持。

NumPy的使用广泛，几乎是所有使用Python进行数据科学的项目的基础库之一。

2.NumPy的使用方法

以下是Numpy库的常用方法，以下代码可直接复制到jupyter notebook运行。

生成随机数组：

# 构造4x4的随机数组
from numpy import *
random.rand(4,4)

# 输出：
'''
array([[0.99764728, 0.06364547, 0.02182546, 0.16433105],
       [0.63289943, 0.29763976, 0.58491023, 0.28307729],
       [0.42512921, 0.27926124, 0.11818588, 0.58845666],
       [0.07451536, 0.65541451, 0.50638315, 0.27005101]])
'''

将数组转换成矩阵matrix：

# 调用mat函数将数组转换成矩阵matrix
randMat=mat(random.rand(4,4))
randMat
# 输出：
'''
matrix([[0.27496011, 0.9093084 , 0.0018111 , 0.13143669],
        [0.85885902, 0.94750823, 0.96820938, 0.06107537],
        [0.67165439, 0.69433003, 0.82237952, 0.25712598],
        [0.65327732, 0.30190633, 0.65090624, 0.05763251]])
'''

求矩阵的逆矩阵：

# 矩阵求逆运算
randMat.I

# 输出：
'''
matrix([[-2.27475911,  1.74370229,  0.3710643 , -0.63203529],
        [ 1.15524442,  0.27630249, -1.52858325,  1.38871436],
        [ 2.0517843 , -2.27912633,  0.3015267 ,  3.06149341],
        [ 0.98720611, -0.61572784,  0.95857182, -0.9405201 ]])
'''

矩阵乘法：

# 矩阵乘法
invRandmat=randMat.I
randMat*invRandmat
# 输出：
'''
matrix([[ 1.00000000e+00,  0.00000000e+00,  8.32667268e-17,
         -1.59594560e-16],
        [ 0.00000000e+00,  1.00000000e+00, -1.66533454e-16,
          1.11022302e-16],
        [-1.11022302e-16,  2.22044605e-16,  1.00000000e+00,
          1.11022302e-16],
        [ 0.00000000e+00,  4.51028104e-17,  0.00000000e+00,
          1.00000000e+00]])
'''

用矩阵与逆矩阵相乘（得到单位阵，实际存在误差）：

# 矩阵乘以其逆矩阵应该是单位矩阵
myEye=randMat*invRandmat  # 矩阵乘其逆矩阵，结果应为单位阵
myEye-eye(4)  # eye(4)将得到一个4阶单位阵
# 输出：
'''
matrix([[ 0.00000000e+00,  0.00000000e+00,  8.32667268e-17,
         -1.59594560e-16],
        [ 0.00000000e+00,  0.00000000e+00, -1.66533454e-16,
          1.11022302e-16],
        [-1.11022302e-16,  2.22044605e-16,  0.00000000e+00,
          1.11022302e-16],
        [ 0.00000000e+00,  4.51028104e-17,  0.00000000e+00,
          0.00000000e+00]])
'''

shape（）函数获得数组的形状：

# shape函数是numpy.core.fromnumeric中的函数，它的功能是读取矩阵的长度，比如shape[0]就是读取矩阵第一维度的长度。
e=eye(3)
e.shape[0]

# 输出：
'''
3
'''

x=random.rand(4,3)  # 生成一个4x3的数组
x.shape[0]
# 输出：
'''
4
'''

numpy tile方法：numpy.tile(A,B)，将重复A数组B次，这里的B可以时int类型也可以是元组类型。

# tile方法
tile([1,2],5)  # 列方向重复5次，行默认1次
# 输出：
'''
array([1, 2, 1, 2, 1, 2, 1, 2, 1, 2])
'''

# tile方法
tile([1,2],(2,1))  # 列方向重复2次，行1次
# 输出：
'''
array([[1, 2],
       [1, 2]])
'''

zeros（）函数创建0数组：

# zeros函数
zeros(5)
# 输出：
'''
array([0., 0., 0., 0., 0.])
'''

# zeros函数
zeros([2,3])
# 输出：
'''
array([[0., 0., 0.],
       [0., 0., 0.]])
'''

3.KNN算法

# kNN算法
from numpy import *  # 从NumPy库导入所有功能模块
import operator  # 该模块包含一系列对标准运算符的函数化实现例如加法乘法等
def CreateDataSet():
    group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])  # 一个NumPy数组，包含了四个二维坐标点。这些点是数据集中的样本
    labels=['A','A','B','B']  # 包含了与 group 数组中每个点相对应的类别标签
    return group,labels  # 返回两个值，group数组和labels列表

group,labels=CreateDataSet()  # 将返回的两个值赋值给group和labels变量
group
# 输出：
'''
array([[1. , 1.1],
       [1. , 1. ],
       [0. , 0. ],
       [0. , 0.1]])
'''

labels
# 输出：
'''
['A', 'A', 'B', 'B']
'''

def  classify0(inX,dataSet,labels,k):  # inX：需要分类的输入样本；dataSet：训练数据集，包含多个已知分类的点；labels：训练数据集中每个点对应的标签；k：在kNN算法中，决定“邻居”数量的参数
    dataSetSize=dataSet.shape[0]  # 获取数据集的行数即样本数量
    print(dataSetSize)
    diffMat=tile(inX,(dataSetSize,1))-dataSet # 将输入的点与训练样本做差，使用 tile 函数将输入向量 inX 复制成与数据集相同大小的矩阵，然后与数据集中的每个点相减，计算输入点与数据集中每个点的差异
    print("这个是dataSet",dataSet)
    print("这个是测试的输入向量",tile(inX,(dataSetSize,1)))
    print("这个是点差",diffMat)
    sqDiffMat=diffMat**2  # 计算出距离平方
    print("这个是距离平方",sqDiffMat)
    sqDistances=sqDiffMat.sum(axis=1)  # 计算距离平方和
    print("这个是距离平方和",sqDistances)
    distances=sqDistances**2  # 开方得出距离
    sortedDistIndicies=distances.argsort()  # 从小到大排序，返回索引
    print("距离排序后对应的索引：",sortedDistIndicies)
    classCount={}  # 初始化一字典来存储每个类别的票数
    for i in range(k):  # 遍历最近的 k 个点，并对其类别进行计票
        voteIlabel=labels[sortedDistIndicies[i]]
        print(voteIlabel)
        classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
    sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)  # 根据票数对类别进行排序
    print(sortedClassCount)
    return sortedClassCount[0][0]
x=classify0([0,0],group,labels,3)  
x

# 输出：
'''
4
这个是dataSet [[1.  1.1]
 [1.  1. ]
 [0.  0. ]
 [0.  0.1]]
这个是测试的输入向量 [[0 0]
 [0 0]
 [0 0]
 [0 0]]
这个是点差 [[-1.  -1.1]
 [-1.  -1. ]
 [ 0.   0. ]
 [ 0.  -0.1]]
这个是距离平方 [[1.   1.21]
 [1.   1.  ]
 [0.   0.  ]
 [0.   0.01]]
这个是距离平方和 [2.21 2.   0.   0.01]
距离排序后对应的索引： [2 3 1 0]
B
B
A
[('B', 2), ('A', 1)]

'B'
'''

4.使用k-近邻算法改进约会网站的配对效果

from numpy import zeros

def file2matrix(filename):
    # 定义标签映射字典
    label_map = {'largeDoses': 2, 'smallDoses': 1, 'didntLike': 0}  # 将字符串标签映射到整数
    fr = open(filename)
    arrayOLines = fr.readlines()  # 用readlines()方法读取文件中的每一行并存储在列表arrayOLines中
    fr.close()  # 读取完数据后应关闭文件
    numberOfLines = len(arrayOLines)  # 获取行数
    # 创建返回的NumPy矩阵, 行数为numberOfLines, 列数固定为3
    returnMat = zeros((numberOfLines, 3))
    classLabelVector = []  # 初始化标签列表
    index = 0
    for line in arrayOLines:
        line = line.strip()  # 去掉每行首尾空白
        listFromLine = line.split('\t')  # 按'\t'分割字符串
        returnMat[index, :] = listFromLine[0:3]  # 前三个元素存入矩阵
        # 使用映射字典获取标签
        classLabelVector.append(label_map[listFromLine[-1]])
        index += 1  # 索引递增，为处理下一行数据做准备
    return returnMat, classLabelVector  # 返回数据矩阵和对应的分类标签

# 调用函数示例
filename = r"F:\桌面\python100\files\data\datingTestSet.txt"
datingDataMat, datingLabels = file2matrix(filename)

# 输出数据矩阵，查看结果
datingDataMat
# 结果矩阵1-3列分别表示：飞行常客里程数、玩视频游戏所耗时间、每周消费的冰激凌数
'''
array([[4.0920000e+04, 8.3269760e+00, 9.5395200e-01],
       [1.4488000e+04, 7.1534690e+00, 1.6739040e+00],
       [2.6052000e+04, 1.4418710e+00, 8.0512400e-01],
       ...,
       [2.6575000e+04, 1.0650102e+01, 8.6662700e-01],
       [4.8111000e+04, 9.1345280e+00, 7.2804500e-01],
       [4.3757000e+04, 7.8826010e+00, 1.3324460e+00]])
'''

结果数据的可视化散点图（取后两维）：

# 制作原始数据的散点图
import matplotlib
import matplotlib.pyplot as plt

fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(datingDataMat[:,1],datingDataMat[:,2])  # 取矩阵的第二列（玩视频游戏所耗时间）、第三列数据（每周消费的冰激凌数）
plt.show()

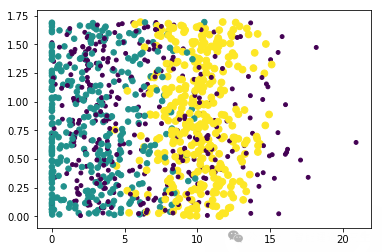
取结果矩阵的后两维特征进行可视化优化：

# 个性化标记散点图上的点
import matplotlib
import matplotlib.pyplot as plt

fig=plt.figure()  # 创建一个图形实例fig
ax=fig.add_subplot(111)  # 向fig添加一个子图 ax，参数 111 表示在一个1x1的网格上创建第一个（也是唯一一个）子图，这是一种快捷方式
ax.scatter(datingDataMat[:,1],datingDataMat[:,2],15.0*array(datingLables),15.0*array(datingLables))  # 将标签数组datingLables转换为NumPy数组，并乘以15.0，目的是让不同的标签对应的点大小有明显区分
plt.show()

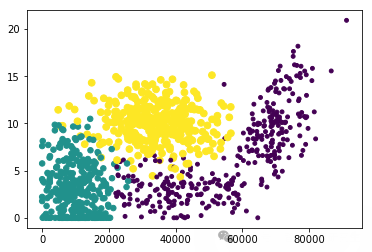
取结果矩阵的前两维特征进行可视化：

# 个性化标记散点图上的点
# 采用列1（飞行常客里程数--x轴）和列2（玩视频游戏时间--y轴）的属性值可以取得更好的效果
import matplotlib
import matplotlib.pyplot as plt

fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(datingDataMat[:,0],datingDataMat[:,1],15.0*array(datingLables),15.0*array(datingLables))  # 分别取数据矩阵的第一列和第二列作为x轴和y轴的数据
plt.show()

---

以上内容总结自网络，如有帮助欢迎转发，我们下次再见！