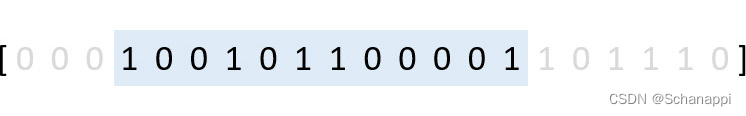题目描述

给你一个整数数组 nums 和一个整数 k 。 nums 仅包含 0 和 1 。每一次移动，你可以选择 相邻 两个数字并将它们交换。
请你返回使 nums 中包含 k 个 连续 1 的 最少 交换次数。

示例 1：

输入：nums = [1,0,0,1,0,1], k = 2
输出：1
解释：在第一次操作时，nums 可以变成 [1,0,0,0,1,1] 得到连续两个 1 。

示例 2：

输入：nums = [1,0,0,0,0,0,1,1], k = 3
输出：5
解释：通过 5 次操作，最左边的 1 可以移到右边直到 nums 变为 [0,0,0,0,0,1,1,1] 。

示例 3：

输入：nums = [1,1,0,1], k = 2
输出：0
解释：nums 已经有连续 2 个 1 了。

提示：

1 <= nums.length <= 10⁵
nums[i] 要么是 0 ，要么是 1 。
1 <= k <= sum(nums)

方法一：滑动窗口，前缀和，步步优化

思路：

• 我们需要移动数组中的 1 ，使得出现连续 k 个 1 ，且移动的次数尽可能少。直接求最优解很困难，因此通过适当的暴力枚举来得到答案。
  直觉上最容易想到：选择 「相邻」（忽略 0 ）的 k 个 1 ，把它们移到一块。这就给 「滑动窗口」这个算法提供了条件，上述所提到的枚举，就是 枚举滑动窗口 。

1. 总体思路

• 找出所有满足条件的窗口，条件是 **窗口内正好有 k 个 1 ，且窗口两个端点都是 1 ** ；
• 对于每个窗口， 求出把其中 k 个 1 移到一块的最小 cost ， 并更新全局最优解 minCost 。
  

2. 给定一个窗口，如何求解「 该窗口的最优解 」？
   

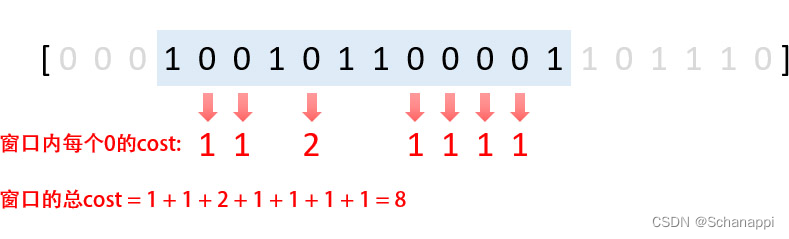
• 以上图中的第一个窗口为例：
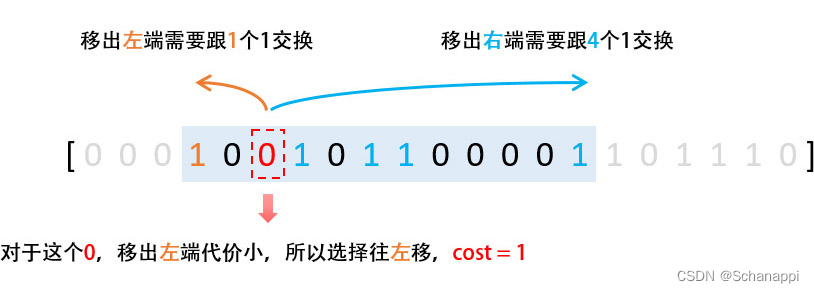
• 把所有 1 移到一起，其实就是把 0 往窗口两端移动 。对于每个 0 ，只有左移和右移两种选择。
  
• 对于每个 0 ，我们都能得到它的 cost ，那么整个窗口的 cost ，就是这些 0 的 cost 之和。
  

3. 算法优化
   上述方法的时间复杂度很高，因此需要进行优化。
   ———
   3.1 合并连续的 0

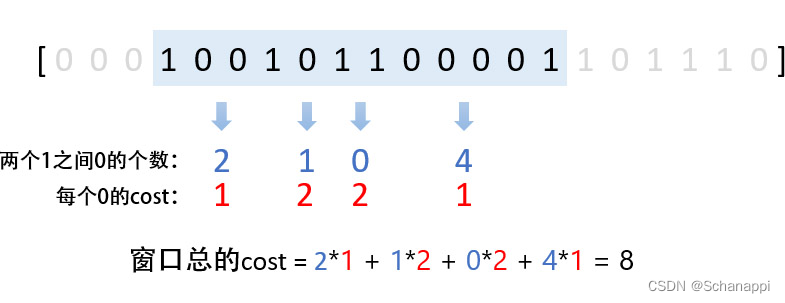
• 对于连续的 0 ，它们的 cost 都是一样的，因此我们可以把加法变成乘法，也就是说，「把连续的 0 ，看作一个整体 0 ， 整体0 的 cost 等于其中每个 0 的 cost 再乘以 0 的个数」
• 需要注意的是，如果两个 1 之间没有 0， 我们就记为零个 0 ， 它的 cost 就是假设中间有 0 时，那些 0 的 cost 。
• 合并 0 之间， 得到一个新数组。
• 这一步的时间复杂度 需要 O（n） ，扫描一遍 nums 就得到。
  ————
  3.2 在 zeros 数组上，计算第一个窗口的解
• 有了 zeros 数组后，我们来算第一个窗口的解。在 zeros 上， 窗口的长度为 k-1 ， 窗口的端点为 [0， k-2] 。
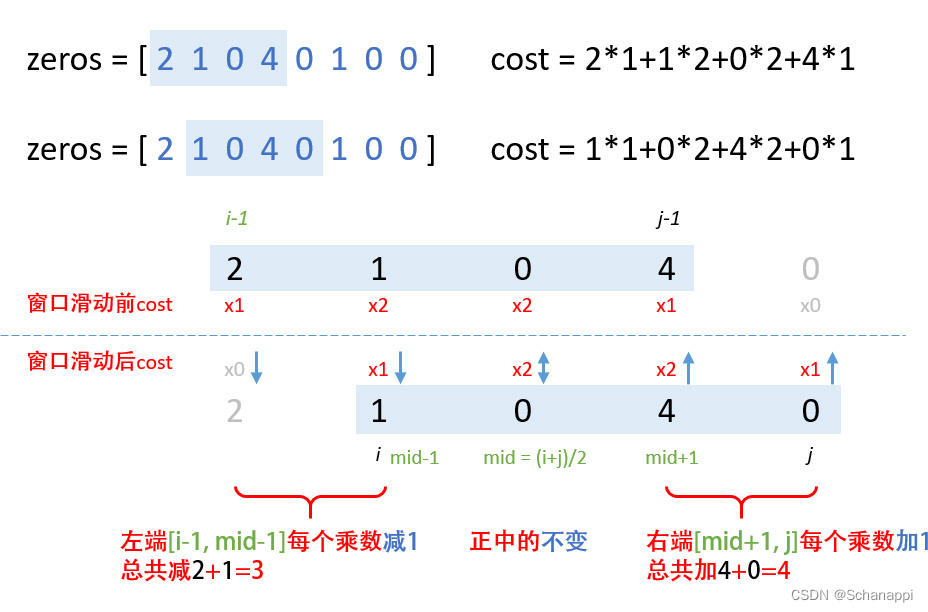
• 对于窗口中每个位置的 cost ，就像是一座山峰，两端是 1 ， 往中间逐个递增。这里第一个窗口的 cost 是 [1, 2, 2, 1] 。把每个位置的 cost 乘上这个位置 0 的个数，就是 zeros[i] ， 再求和就得到窗口整体的 cost 。
• 这一步的时间复杂度 是O（k）。————
  3.3 窗口开始滑动
• 有了 zeros 数组后， 滑动窗口变得简单。在 nums 上，窗口的长度是变化的，而在zeros 上， 窗口的长度则是固定的。
• 第一个窗口的解需要花费O（k）的时间，如果之后每个窗口也都需要花费O（k），那整体的时间复杂度就需要乘以平方了。
• 因此，要利用滑动窗口的特性 ， 「下一个窗口的解，可以由前一个窗口的解快速得到」，如果能在O（1）的时间解决， 那整体就是线性复杂度了。
• Q：如何通过上一个窗口的解求得下一个窗口的解呢？
  • 根据窗口长度的奇偶性，分情况讨论，如果窗口长度是偶数：
  • 假设当前窗口从 i 到 j ，那么上一个窗口就是从 i-1 到 j-1 。我们可以找到一个中点 mid ，它左边的 cost 都减少 1 ， 右边的 cost 都增加 1 。 因为减少或增加的 1 需要与 zeros 中的值相乘， 所以 cost 的变化可以通过求 zeros 上 「区间和」来快速得到。
    • 通过区间端点（i， j）算出中点坐标 mid；
    • 求出窗口中点左边，即[i-1， mid-1] 范围的区间和；
    • 求出窗口右边，即[mid+1， j] 范围的区间和；
    • 更新 cost。

//窗口长度k-1是偶数的情况
int mid = (i + j) / 2;
cost -= GetRangeSum(i-1, mid-1);
cost += GetRangeSum(mid+1, j);

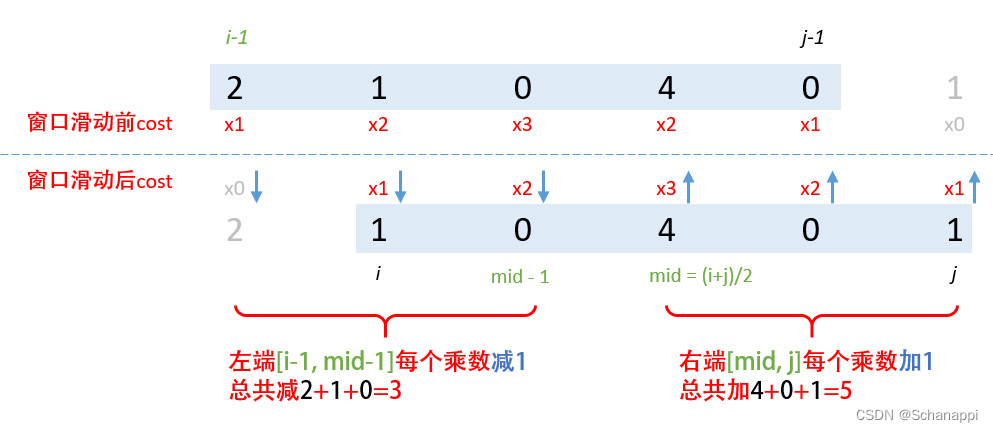
• 如果窗口长度是奇数：
• 只是分割区间的位置稍有不同，大体上还是一致的。
  //窗口长度k-1是奇数的情况
int mid = (i + j) / 2;
cost -= GetRangeSum(i-1, mid-1);
cons += GetRangeSum(mid, j)
• 从代码的简洁性考虑，可以合并奇、偶两种情况，窗口长度是 k-1 ，如果 k-1 是偶数，即 k 是奇数，则右边区间的起点 + 1：
  //合并上述两种情况
int mid = (i + j) / 2;
cost -= GetRangeSum(i-1, mid-1);
cons += GetRangeSum(mid+k%2, j)
• 如果 GetRangeSum() 的时间复杂度为O（1），那么更新窗口的时间复杂度也就是O（1），窗口从头滑到尾，整体就是线性复杂度O（n）。
  ——————
  3.4 数组的区间和
• 最后一个目标，就是实现常数复杂度的 GetRangeSum() 。通过预先处理，构造出 「前缀和」 数组后，就可以在O（1）时间内得到区间和。

情况

• 通过；

收获

• 这道题用到的知识点太多了，也很难，今天可能花了2个小时，甚至不止，在这道题上，并且不算特别明白。有空需要多看看。

时间复杂度：O（n）
空间复杂度：O（n）

class Solution {
private:
    vector<int> zeros;
    vector<int> pre {0}; 

    void GenerateZeros(const vector<int> &nums){
        int n = nums.size(), i = 0;
        while(i < n && nums[i] == 0) i++ ;
        while(i < n){
            int j = i + 1;
            while(j < n && nums[j] == 0) j ++;
            if(j < n) zeros.push_back(j - i -1);
            i = j;
        }
    }
    void GeneratePresum(vector<int>& zeros){
        for(int i=0; i<zeros.size(); i++){
            pre.push_back(pre.back() + zeros[i]); 
        }
    }
    int GetRangeSum(int left, int right){
        return pre[right+1] - pre[left];
    }
public:
    int minMoves(vector<int>& nums, int k) {
        // 计算数组 zeros
        GenerateZeros(nums);

        int cost = 0;
        int left = 0, right = k - 2;
        for(int i=left; i<=right; i++){
            cost += zeros[i] * (min(i+1, right-i+1));
        }

        int minCost = cost;

        GeneratePresum(zeros);
        int i=1, j = i + k - 2;
        for(; j<zeros.size(); i++, j++){
            int mid=(i + j) / 2;
            cost -= GetRangeSum(i-1, mid-1);
            cost += GetRangeSum(mid+k%2, j);
            minCost = min(minCost, cost);
        }
        return minCost;
    }
};

参考题解：

1. 【多图】新手教程，一步步带你写，把Hard分解成Easy