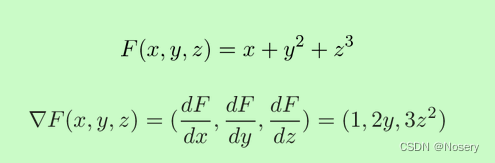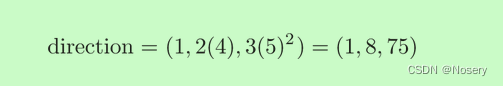BetterExplained – Math lessons that click 

一、复数

i 的物理意义就是旋转，i 就是逆时针旋转90°，i*i 就是逆时针旋转180°

加法：实部相加，虚部相加

乘法：

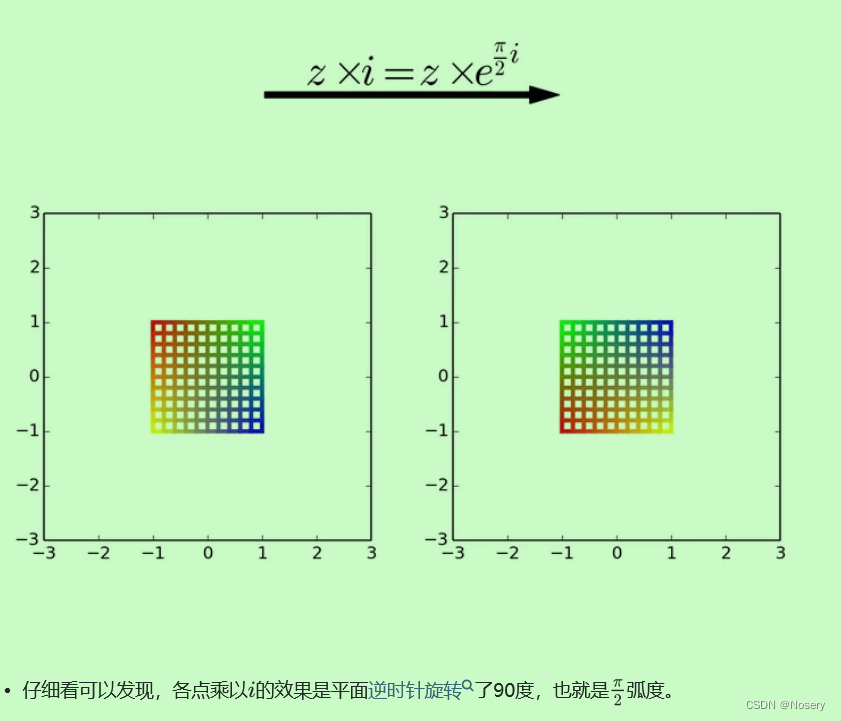
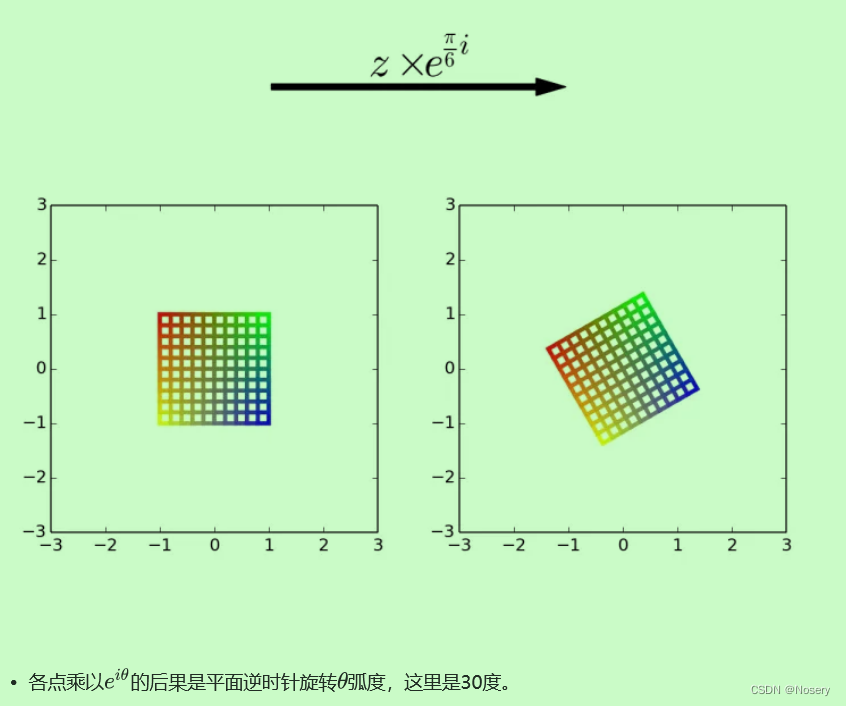
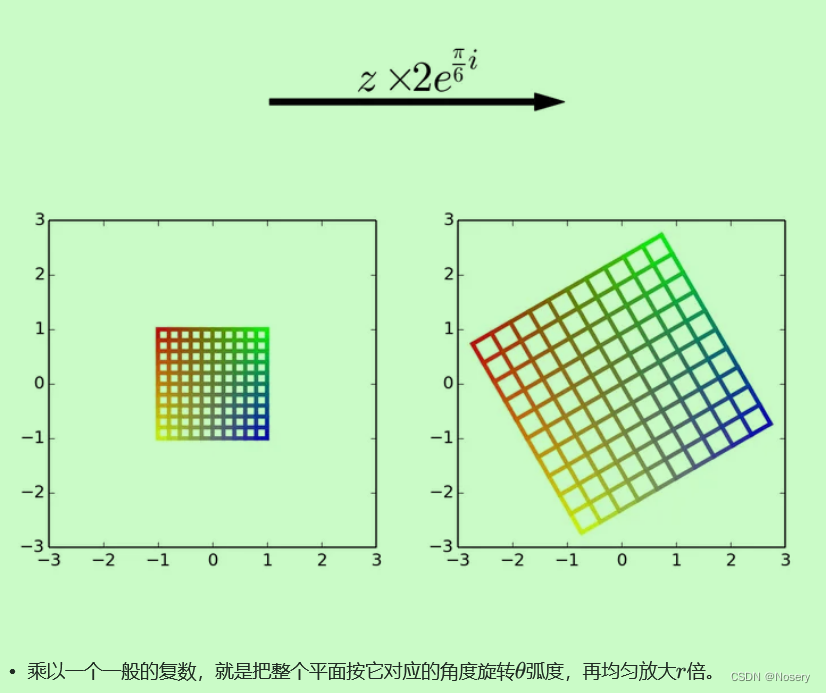
复数z=x+yi控制了函数的放缩和旋转 ——x 放缩，y 旋转（即放缩e^x倍，旋转y弧度）

在x轴上不旋转，在y轴上不放缩——因为此时对应的 yi 和 x 均为0

二、导数

• 导数在数学上反映的是一点的斜率，概率论上可以反映一点的
• 在物理上反映的是物理量随时间变化的情况，集中到一点就反映该点随时间变化的快慢
• 在大小上反映的是小空间上的变换的伸缩倍数，正负号反映在小空间内是否反向

偏导数反映了多元函数在不同数轴上的变化率；方向导数则反映了任意方向上的导数；梯度反映函数最快的增长方向，逆梯度则表示最快的下降方向，故梯度下降法也称为最速下降法

1、偏导数

对函数 z=f(x,y)=x²+xy+y² 的偏导数：

z对x的偏导数∂z/∂x=2x+y —— 将y看作常量；z对y的偏导数∂z/∂y=x+2y —— 将x看作常量

高阶偏导数就是对导数再求导

拉普拉斯方程

方程的解称为调和函数——满足Laplace方程的函数为调和函数

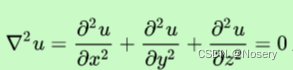
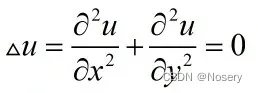
2、方向导数

方向导数是偏导数的特殊情况，因为方向导数是在任意方向的导数，在一空间里，任意的方向都可以使用坐标轴唯一的表示

其求法为根据题意确定方向的单位向量，如x轴负方向的方向向量为（-1,0,0），则和该单位向量数学表达一 一对应

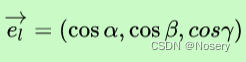
与各个方向上的偏导数乘积的和就是函数在某个方向上的方向导数

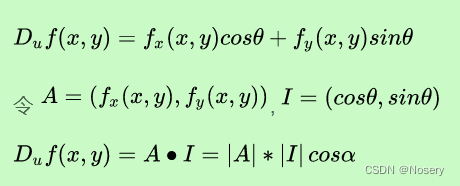
3、梯度

梯度指F因为x，y，z的移动而改变了多少，是函数的最大增长方向 —— 在每个方向上的运动使函数获得最大增益

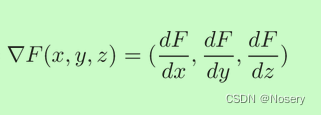
给定坐标带入梯度后就是函数当前位置要增加到最大值的方向