目录
一、直接插入排序
(一)单趟直接插入排
1.分析+核心代码
2.完整代码
(二)全部直接插入排
1.分析+核心代码
2.完整代码
(三)时间复杂度和空间复杂度
二、希尔排序
(一)对一组数据进行直接插入排序
(二)对每个分组分别进行直接插入排序
(三)对每个分组同时进行直接插入排序
(四)可变的gap
(五)时间复杂度和空间复杂度
三、直接选择排序
(一)找一个最小值
1、单趟直接选择排序
2、多趟选择排序
3、时间复杂度和空间复杂度
(二)同时找最小值和最大值
1、单趟直接选择排序
2、多趟选择排序
3、时间复杂度和空间复杂度
四、冒泡排序
(一)核心代码
(二)完整代码
(三)时间复杂度
五、快速排序
(一)Hoare
1. 易出错分析——死循环
2. 易出错分析——越界
3. 一次快排核心代码
4. 递归核心代码
5. 测试代码
6. 时间复杂度
(二)挖坑法
1. 单趟挖坑的代码
2. 单趟测试代码
3. 递归挖坑代码
4. 递归挖坑测试代码
(三)前后指针
1. 单趟核心代码
2. 单趟测试代码
3. 递归核心代码
4. 递归测试代码
(四)非递归实现(栈)
六、归并排序
1. 递归核心代码
2. 测试代码
3. 非递归核心代码
4. 测试代码
七、堆排序
1. 向下调整
2. 建堆
3. 堆排序代码
4. 向上调整
5. 测试
一、直接插入排序
(一)单趟直接插入排
1.分析+核心代码
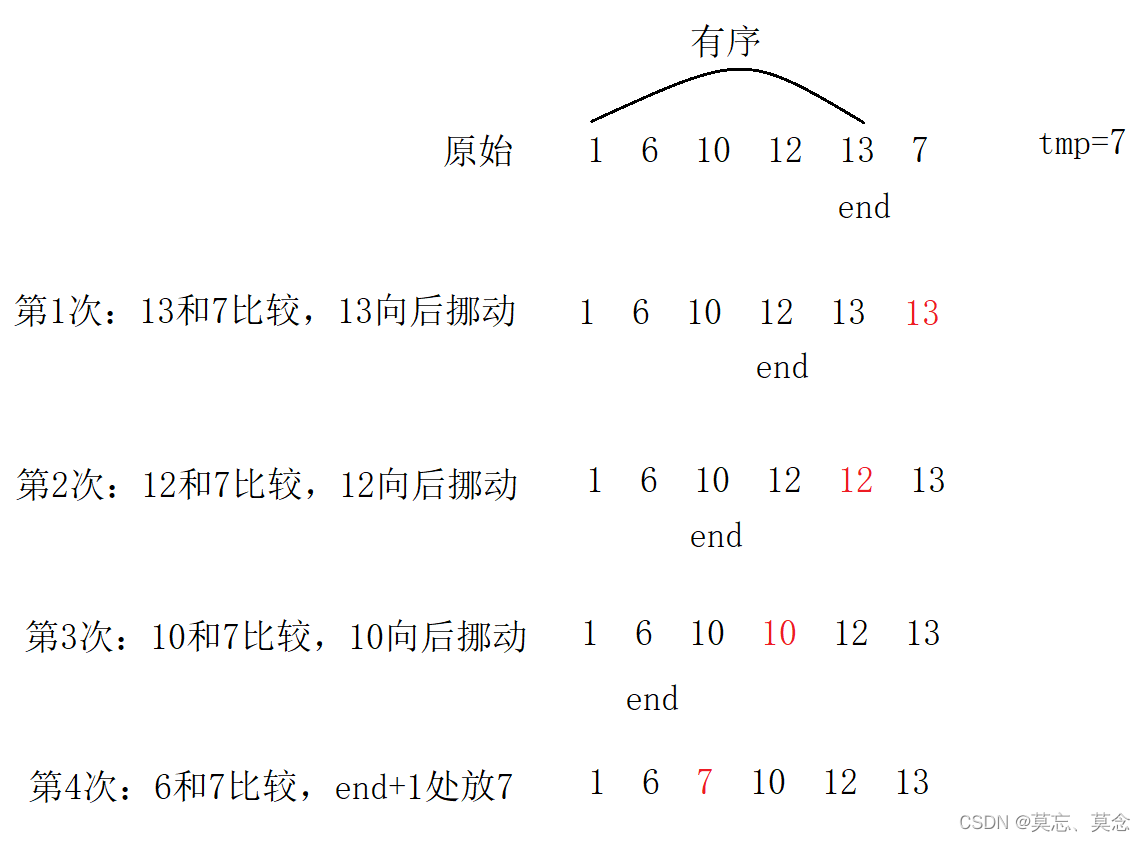
void InsertSort(int* data, int n)
{
//[0,end]有序
int end = n - 2;
int tmp = data[end+1];
while (end >= 0)//升序
{
if (data[end] > tmp)
{
data[end + 1] = data[end];
--end;
}
else
{
break;
}
}
data[end + 1] = tmp;
}2.完整代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void InsertSort(int* data, int n)
{
//[0,end]有序
int end = n - 2;
int tmp = data[end+1];
while (end >= 0)//升序
{
if (data[end] > tmp)
{
data[end + 1] = data[end];
--end;
}
else
{
break;
}
}
data[end + 1] = tmp;
}
void Print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
}
int main()
{
int a[] = { 1,6,10,12,13,7 };
InsertSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
return 0;
}(二)全部直接插入排
1.分析+核心代码
- 红色线条前的数据依次和tmp比较,比tmp大就往后面挪动
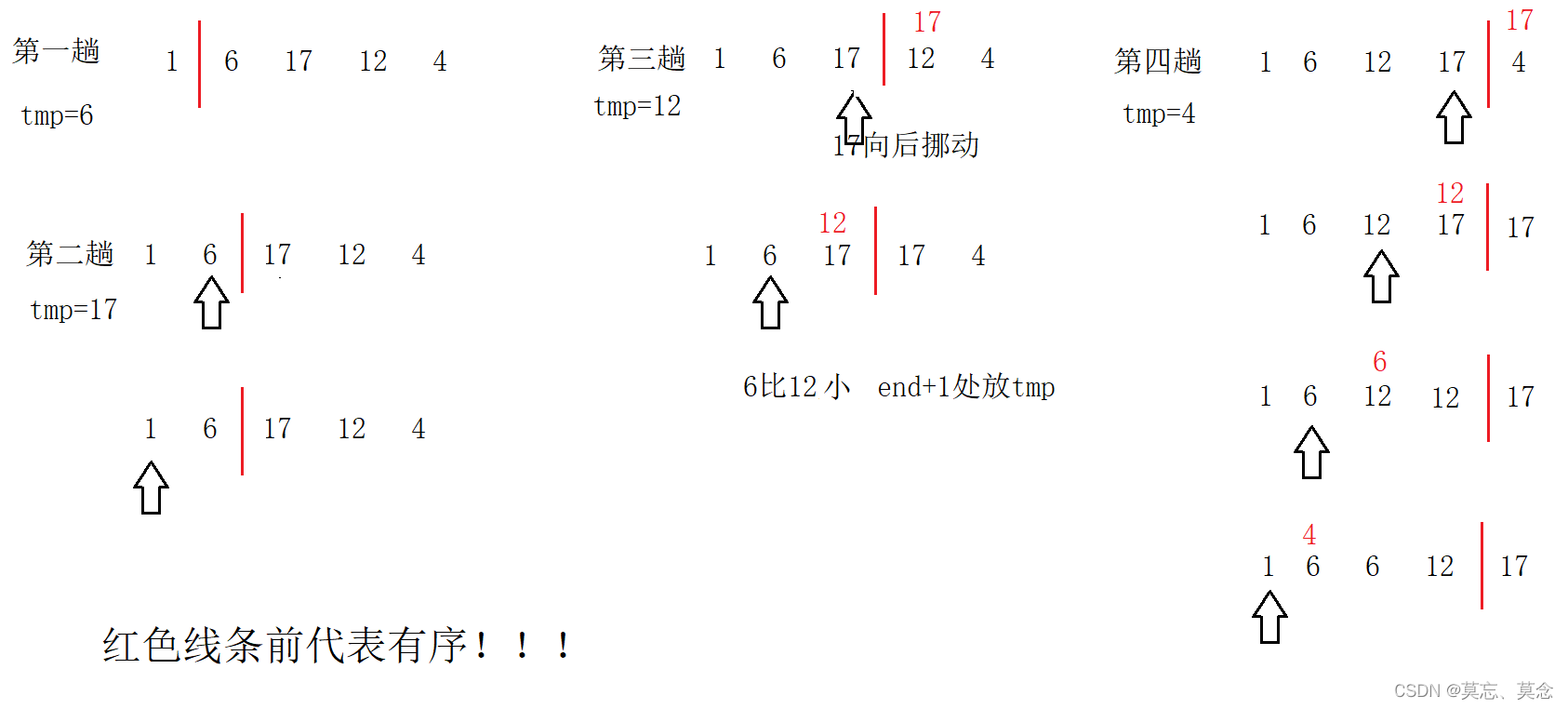
void InsertSort(int* data, int n)
{
for (int i = 0; i < n-1; i++)
{
int end = i;
int tmp = data[end+1];
while (end >= 0)//升序
{
if (data[end] > tmp)
{
data[end + 1] = data[end];
--end;
}
else
{
break;
}
}
data[end + 1] = tmp;
}
}2.完整代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void InsertSort(int* data, int n)
{
for (int i = 0; i < n-1; i++)
{
int end = i;
int tmp = data[end+1];
while (end >= 0)//升序
{
if (data[end] > tmp)
{
data[end + 1] = data[end];
--end;
}
else
{
break;
}
}
data[end + 1] = tmp;
}
}
void Print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
}
int main()
{
int a[] = { 1,6,17,12,4 };
InsertSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
return 0;
}(三)时间复杂度和空间复杂度

二、希尔排序
(一)对一组数据进行直接插入排序
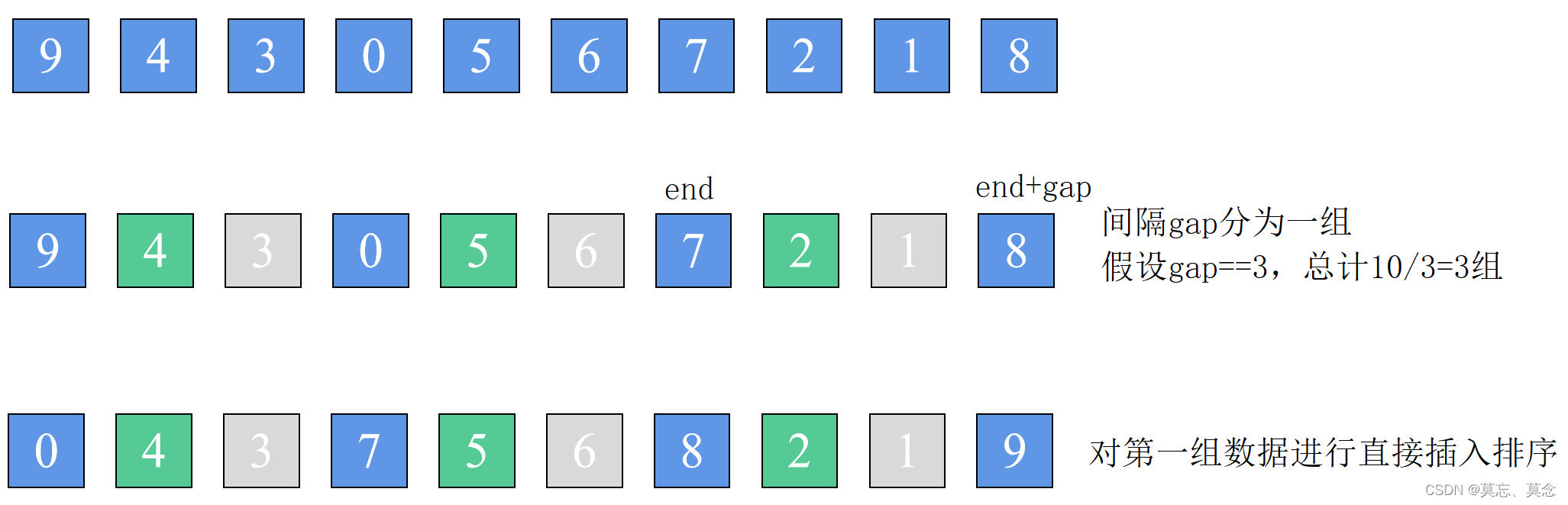

void ShellSort(int* data, int n)
{
int gap = 3;
for (int i = 0; i+gap < n; i+=gap)//对第一组数据进行插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void ShellSort(int* data, int n)
{
int gap = 3;
for (int i = 0; i+gap < n; i+=gap)//对第一组数据进行插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}
void Print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
int main()
{
int a[] = { 9,4,3,0,5,6,7,2,1,8 };
ShellSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
return 0;
}(二)对每个分组分别进行直接插入排序


void ShellSort(int* data, int n)
{
int gap = 3;
for (int k = 0; k < gap; k++)//一共有gap组
{
for (int i = k; i + gap < n; i += gap)//对第k组数据进行插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}
}#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void ShellSort(int* data, int n)
{
int gap = 3;
for (int k = 0; k < gap; k++)//一共有gap组
{
for (int i = k; i + gap < n; i += gap)//对第k组数据进行插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}
}
void Print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
int main()
{
int a[] = { 9,4,3,0,5,6,7,2,1,8 };
ShellSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
return 0;
}(三)对每个分组同时进行直接插入排序
void ShellSort(int* data, int n)
{
int gap = 3;
for (int i = 0; i + gap < n; i++)//对多组同时进行直接插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void ShellSort(int* data, int n)
{
int gap = 3;
for (int i = 0; i + gap < n; i++)//对多组同时进行直接插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}
void Print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
int main()
{
int a[] = { 9,4,3,0,5,6,7,2,1,8 };
ShellSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
return 0;
}
(四)可变的gap
void ShellSort(int* data, int n)
{
int gap = n;
while (gap > 1)
{
//1、gap > 1 与排序
//2、gap == 1直接插入排序
gap = gap / 3 + 1;
for (int i = 0; i + gap < n; i++)//对多组同时进行直接插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}
}#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void ShellSort(int* data, int n)
{
int gap = n;
while (gap > 1)
{
//1、gap > 1 与排序
//2、gap == 1直接插入排序
gap = gap / 3 + 1;
for (int i = 0; i + gap < n; i++)//对多组同时进行直接插入排序
{
int end = i;
int tmp = data[end + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end = end - gap;
}
else
break;
}
data[end + gap] = tmp;
}
}
}
void Print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
int main()
{
int a[] = { 9,4,3,0,5,6,7,2,1,8 };
ShellSort(a, sizeof(a) / sizeof(int));
Print(a, sizeof(a) / sizeof(int));
return 0;
}(五)时间复杂度和空间复杂度

三、直接选择排序
- 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。

(一)找一个最小值
1、单趟直接选择排序
- 从待排序列中选出一个最小值,然后放在序列的起始位置
void SelectSort(int* data, int n)
{
int start = 0;//待排序的数据的区间的开始位置
int min_index = start;//最小元素的小标
for (int i = start; i < n; i++)
{
if (data[i] < data[min_index])
{
min_index = i;
}
}
Swap(&data[start], &data[min_index]); //最小值与第一个元素交换位置
}#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void SelectSort(int* data, int n)
{
int start = 0;//待排序的数据的区间的开始位置
int min_index = start;//最小元素的下标
for (int i = start; i < n; i++)
{
if (data[i] < data[min_index])
{
min_index = i;
}
}
Swap(&data[start], &data[min_index]); //最小值与第一个元素交换位置
}
int main()
{
int a[] = { 9,3,6,2,7,4 };
print(a, sizeof(a) / sizeof(int));
SelectSort(a, sizeof(a) / sizeof(int));
print(a, sizeof(a) / sizeof(int));
return 0;
}

2、多趟选择排序
void SelectSort(int* data, int n)
{
for (int k = 0; k < n; k++)//某一趟选择排序从下标为k的元素开始
{
int start = k;//待排序的数据的区间的开始位置
int min_index = start;//最小元素的下标
for (int i = start; i < n; i++)
{
if (data[i] < data[min_index])
{
min_index = i;
}
}
Swap(&data[start], &data[min_index]); //最小值与参与第一个元素交换位置
}
}3、时间复杂度和空间复杂度

(二)同时找最小值和最大值
1、单趟直接选择排序
- 一趟选出两个值,一个最大值一个最小值,分别放在放在开头和结尾
void SelectSort(int* data, int n)
{
int begin = 0;//待排序的数据的区间的开始位置
int end = n - 1;
int min_index = begin;//最小元素的下标
int max_index = end;//最大元素的下标
for (int i = 0; i < n; i++)
{
if (data[i] < data[min_index])
{
min_index = i;
}
if (data[i] > data[max_index])
{
max_index = i;
}
}
Swap(&data[begin], &data[min_index]); //最小值与第一个元素交换位置
if (max_index == begin)//如果最大值在第一个位置处
{
max_index = min_index;
}
Swap(&data[end], &data[max_index]); //最大值和最后一个元素交换位置
//下次调整[1,n-2]之间的数据
}2、多趟选择排序
void SelectSort(int* data, int n)
{
int begin = 0;//待排序的数据的区间的开始位置
int end = n - 1;
while (begin < end)
{
int min_index = begin;//最小元素的下标
int max_index = end;//最大元素的下标
for (int i = begin; i <= end; i++)
{
if (data[i] < data[min_index])
{
min_index = i;
}
if (data[i] > data[max_index])
{
max_index = i;
}
}
Swap(&data[begin], &data[min_index]); //最小值与第一个元素交换位置
if (max_index == begin)//如果最大值在第一个位置处
{
max_index = min_index;
}
Swap(&data[end], &data[max_index]); //最大值和最后一个元素交换位置
//下次调整[1,n-2]之间的数据
begin++;
end--;
}
}#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void SelectSort(int* data, int n)
{
int begin = 0;//待排序的数据的区间的开始位置
int end = n - 1;
while (begin < end)
{
int min_index = begin;//最小元素的下标
int max_index = end;//最大元素的下标
for (int i = begin; i <= end; i++)
{
if (data[i] < data[min_index])
{
min_index = i;
}
if (data[i] > data[max_index])
{
max_index = i;
}
}
Swap(&data[begin], &data[min_index]); //最小值与第一个元素交换位置
if (max_index == begin)//如果最大值在第一个位置处
{
max_index = min_index;
}
Swap(&data[end], &data[max_index]); //最大值和最后一个元素交换位置
//下次调整[1,n-2]之间的数据
begin++;
end--;
}
}
int main()
{
int a[] = { 9,3,6,2,7,4 };
print(a, sizeof(a) / sizeof(int));
SelectSort(a, sizeof(a) / sizeof(int));
print(a, sizeof(a) / sizeof(int));
return 0;
}
3、时间复杂度和空间复杂度

四、冒泡排序
- 基本思想:从第一个元素开始,比较相邻元素的大小,若大小有误,则对调再进行下一个元素的比较,如此扫过依次之后就可以确保最后一个元素位于正确的顺序。接着进行第二次扫描
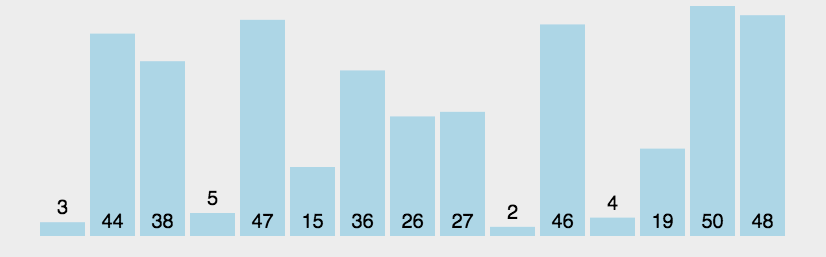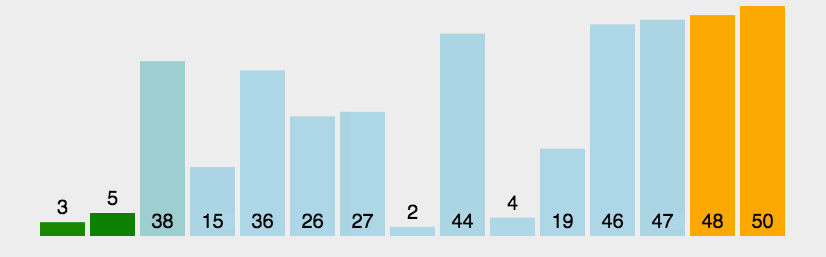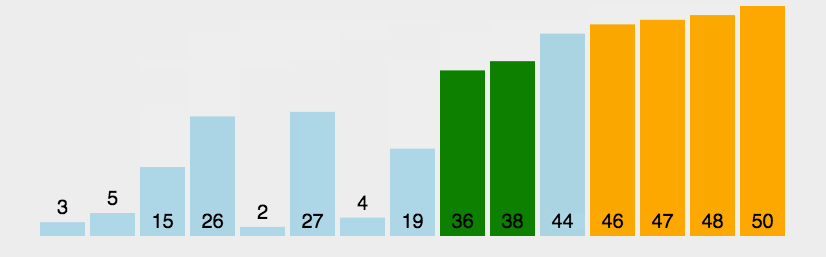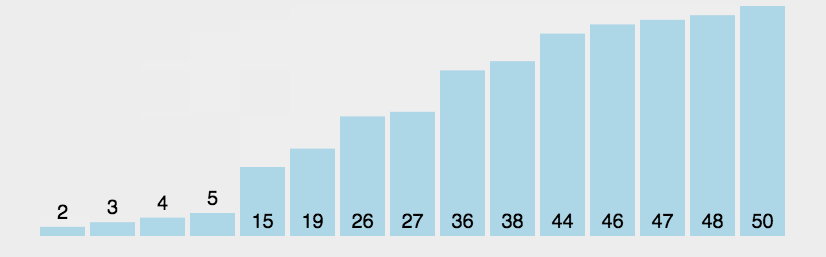
(一)核心代码
void BubbleSort(int* data, int n)
{
for (int end = n - 1; end >= 0; end--)//每次将数据交换到下标为end的位置处
{
bool exchange = false;
for (int i = 0; i < end; i++)//[i,end-1]
{
if (data[i] > data[i + 1])
{
Swap(&data[i], &data[i + 1]);
exchange = true;
}
}
if (exchange == false)
break;
}
}(二)完整代码
#include<stdio.h>
#include<stdbool.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void BubbleSort(int* data, int n)
{
for (int end = n - 1; end >= 0; end--)//每次将数据交换到下标为end的位置处
{
bool exchange = false;
for (int i = 0; i < end; i++)//[i,end-1]
{
if (data[i] > data[i + 1])
{
Swap(&data[i], &data[i + 1]);
exchange = true;
}
}
if (exchange == false)
break;
}
}
int main()
{
int a[] = { 9,3,6,2,7,4 };
//int a[] = { 1,2,3,4,5,6 };
print(a, sizeof(a) / sizeof(int));
BubbleSort(a, sizeof(a) / sizeof(int));
print(a, sizeof(a) / sizeof(int));
return 0;
}(三)时间复杂度

五、快速排序
(一)Hoare
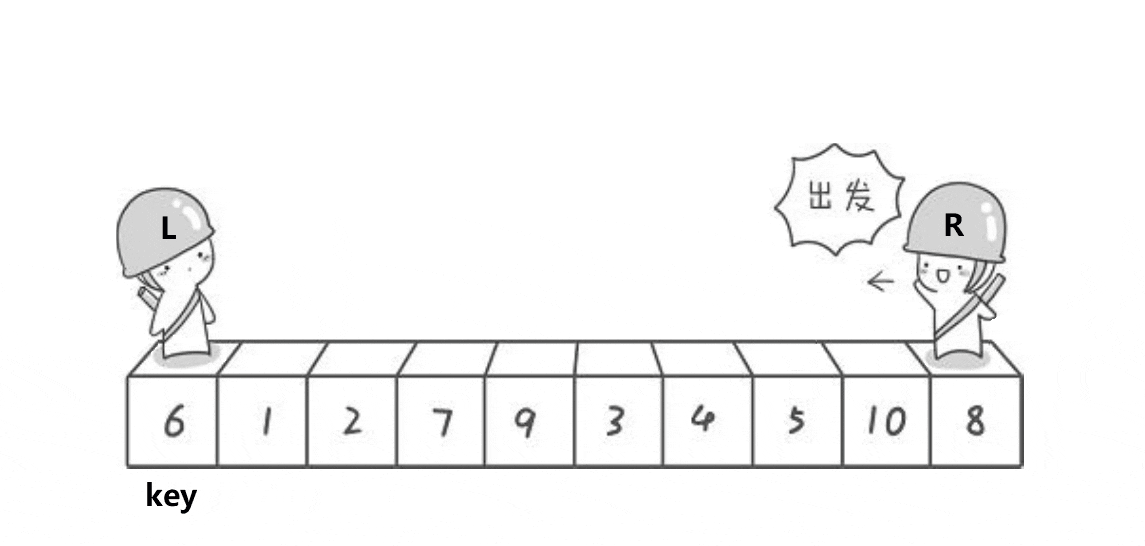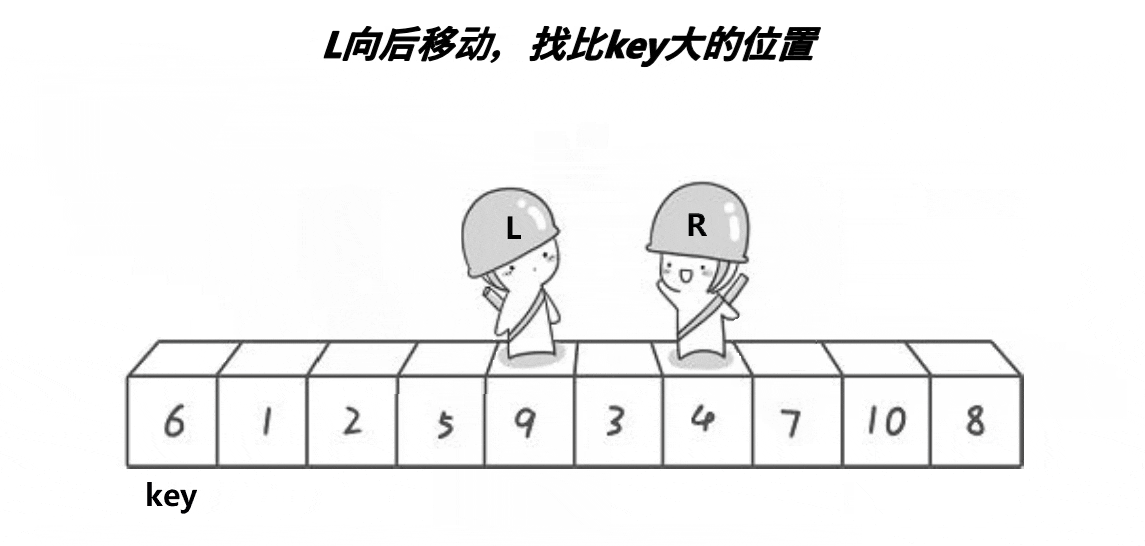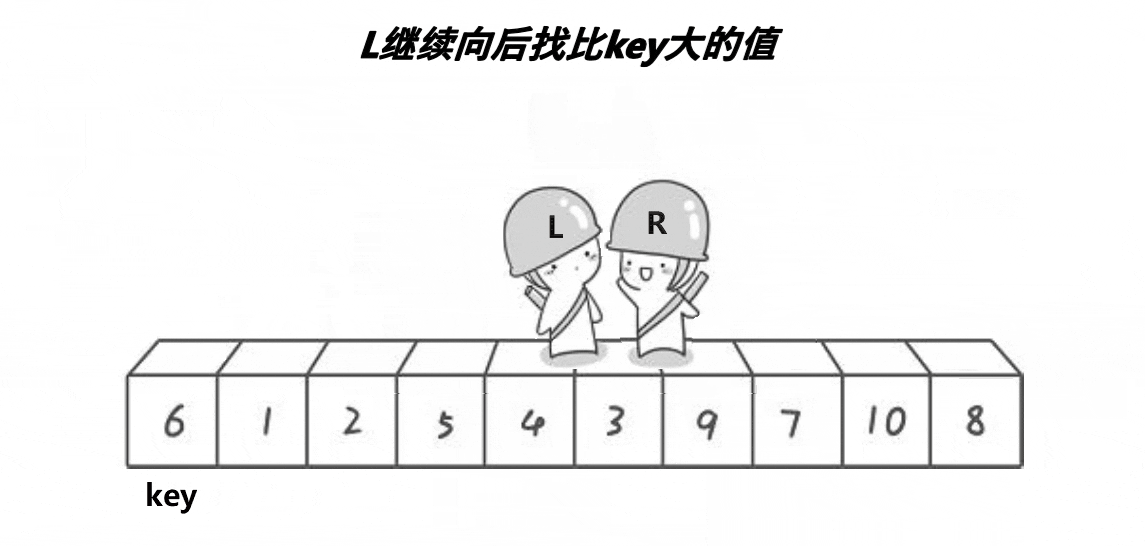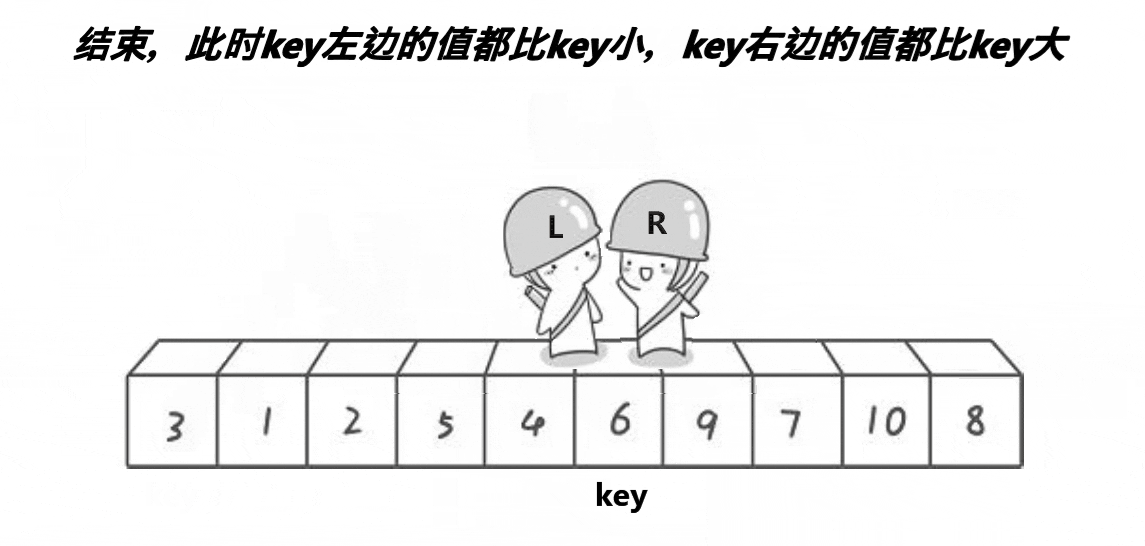
1. 易出错分析——死循环


2. 易出错分析——越界

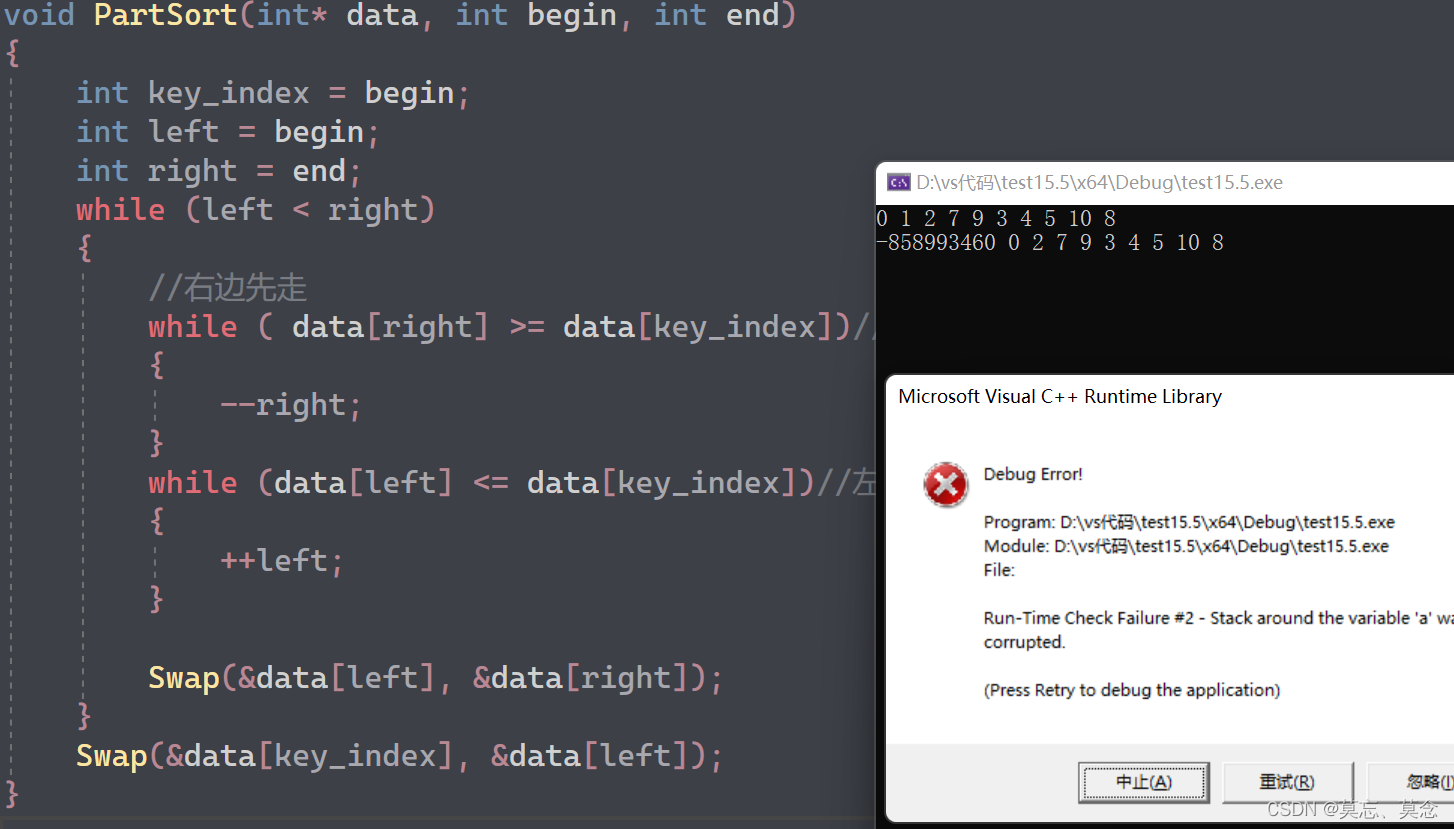
3. 一次快排核心代码
int PartSort(int* data, int begin, int end)
{
int key_index = begin;
int left = begin;
int right = end;
while (left < right)
{
//右边先走
while (left < right && data[right] >= data[key_index])//右边找小
{
--right;
}
while (left < right && data[left] <= data[key_index])//左边找大
{
++left;
}
Swap(&data[left], &data[right]);
}
Swap(&data[key_index], &data[left]);
return left;//返回相遇点,key的当前下标
}4. 递归核心代码
void QuickSort(int* data, int begin, int end)
{
if (begin >= end)//当只有一个数据或是数组不存在时,不需要进行操作
return;
int key_index = begin;
int left = begin;
int right = end;
while (left < right)
{
//右边先走
while (left < right && data[right] >= data[key_index])//右边找小
{
--right;
}
while (left < right && data[left] <= data[key_index])//左边找大
{
++left;
}
Swap(&data[left], &data[right]);
}
//此时left=right
Swap(&data[key_index], &data[left]);
QuickSort(data, begin, left - 1);//左区间
QuickSort(data, left+1,end);//右区间
}5. 测试代码
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void QuickSort(int* data, int begin, int end)
{
if (begin >= end)//当只有一个数据或是数组不存在时,不需要进行操作
return;
int key_index = begin;
int left = begin;
int right = end;
while (left < right)
{
//右边先走
while (left < right && data[right] >= data[key_index])//右边找小
{
--right;
}
while (left < right && data[left] <= data[key_index])//左边找大
{
++left;
}
Swap(&data[left], &data[right]);
}
//此时left=right
Swap(&data[key_index], &data[left]);
QuickSort(data, begin, left - 1);//左区间
QuickSort(data, left+1,end);//右区间
}
int main()
{
//int a[] = {6,1,2,7,9,3,4,5,10,8 };
int a[] = {6,1,2,7,9,3,4,5,10,8 };
print(a, sizeof(a) / sizeof(int));
QuickSort(a, 0,sizeof(a) / sizeof(int)-1);
print(a, sizeof(a) / sizeof(int));
return 0;
}6. 时间复杂度

(二)挖坑法


1. 单趟挖坑的代码
int PartSort(int* data, int left, int right)
{
int key = data[left];
int hole = left;//最左边坑所在的下标
while (left < right)
{
while (left<right && data[right]>=key)//右边找小
{
--right;
}
data[hole] = data[right];//填坑
hole = right;//更新坑位
while (left < right && data[left] <= key)//左边找大
{
++left;
}
data[hole] = data[left];
hole = left;//更新坑位
}
data[hole] = key;
return hole;//返回此时key的下标
}2. 单趟测试代码
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
int PartSort(int* data, int left, int right)
{
int key = data[left];
int hole = left;//最左边坑所在的下标
while (left < right)
{
while (left < right && data[right] >= key)//右边找小
{
--right;
}
data[hole] = data[right];//填坑
hole = right;//更新坑位
while (left < right && data[left] <= key)//左边找大
{
++left;
}
data[hole] = data[left];
hole = left;//更新坑位
}
data[hole] = key;
return hole;//返回此时key的下标
}
int main()
{
//int a[] = {6,1,2,7,9,3,4,5,10,8 };
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
print(a, sizeof(a) / sizeof(int));
int x =PartSort(a, 0, sizeof(a) / sizeof(int) - 1);
printf("%d\n", x);
print(a, sizeof(a) / sizeof(int));
return 0;
}3. 递归挖坑代码
void QuickSort(int* data, int begin, int end)
{
if (begin >= end)
return;
int left = begin;
int right = end;
int key = data[left];
int hole = left;//最左边坑所在的下标
while (left < right)
{
while (left < right && data[right] >= key)//右边找小
{
--right;
}
data[hole] = data[right];//填坑
hole = right;//更新坑位
while (left < right && data[left] <= key)//左边找大
{
++left;
}
data[hole] = data[left];
hole = left;//更新坑位
}
data[hole] = key;
QuickSort(data, begin, hole - 1);//递归左边
QuickSort(data, hole +1,end);//递归右边
}4. 递归挖坑测试代码
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void QuickSort(int* data, int begin, int end)
{
if (begin >= end)
return;
int left = begin;
int right = end;
int key = data[left];
int hole = left;//最左边坑所在的下标
while (left < right)
{
while (left < right && data[right] >= key)//右边找小
{
--right;
}
data[hole] = data[right];//填坑
hole = right;//更新坑位
while (left < right && data[left] <= key)//左边找大
{
++left;
}
data[hole] = data[left];
hole = left;//更新坑位
}
data[hole] = key;
QuickSort(data, begin, hole - 1);//递归左边
QuickSort(data, hole +1,end);//递归右边
}
int main()
{
//int a[] = {6,1,2,7,9,3,4,5,10,8 };
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
print(a, sizeof(a) / sizeof(int));
QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
print(a, sizeof(a) / sizeof(int));
return 0;
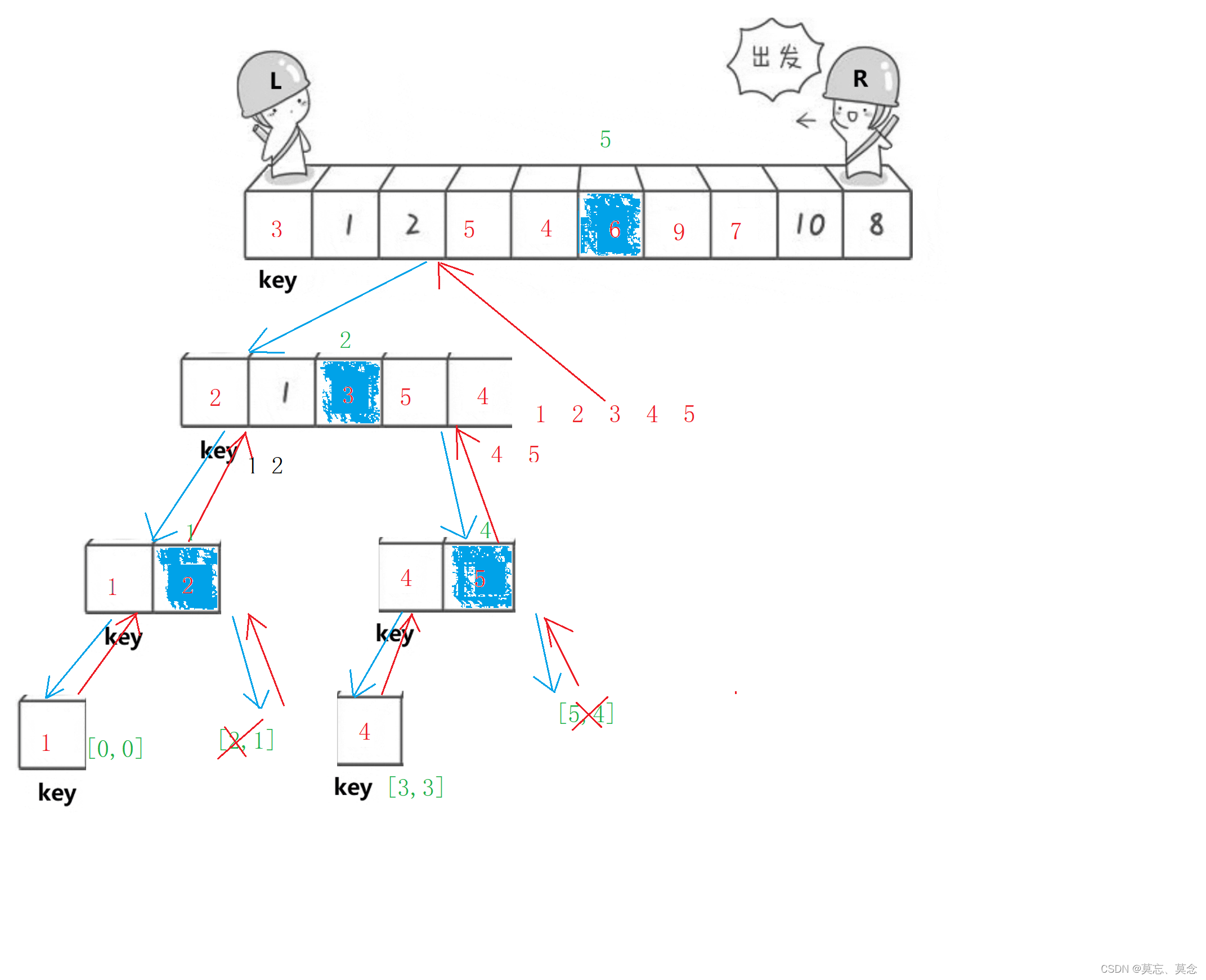
}(三)前后指针

- 最开始prev和cur相邻
- 当cur遇到比key大的值后,他们之间的值都是比key大的值
- 当cur找小,找到小的以后与++prev位置的值交换,相当于把大的值翻滚式向右边推,同时把小的换到左边
1. 单趟核心代码
int PartSort(int* data, int left, int right)
{
int prev = left;
int cur = left + 1;
int key_index = left;
while (cur <= right)
{
if (data[cur] < data[key_index] && ++prev != cur)//如果prev和cur指向同一个数据没必要交换
{
Swap(&data[cur], &data[prev]);
}
++cur;
}
Swap(&data[key_index], &data[prev]);
key_index = prev;
return key_index;
}2. 单趟测试代码
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
int PartSort(int* data, int left, int right)
{
int prev = left;
int cur = left + 1;
int key_index = left;
while (cur <= right)
{
if (data[cur] < data[key_index] && ++prev != cur)//如果prev和cur指向同一个数据没必要交换
{
Swap(&data[cur], &data[prev]);
}
++cur;
}
Swap(&data[key_index], &data[prev]);
key_index = prev;
return key_index;
}
int main()
{
//int a[] = {6,1,2,7,9,3,4,5,10,8 };
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
print(a, sizeof(a) / sizeof(int));
int x = PartSort(a, 0, sizeof(a) / sizeof(int) - 1);
printf("%d\n", x);
print(a, sizeof(a) / sizeof(int));
return 0;
}3. 递归核心代码
void QuickSort(int* data, int begin, int end)
{
if (begin >= end)
return;//结束条件
int prev = begin;
int cur = begin + 1;
int key_index = begin;
while (cur <= end)
{
if (data[cur] < data[key_index] && ++prev != cur)//如果prev和cur指向同一个数据没必要交换
{
Swap(&data[cur], &data[prev]);
}
++cur;
}
Swap(&data[key_index], &data[prev]);
key_index = prev;//cur越界时,prev的位置
QuickSort(data, begin, key_index-1);//递归排序左边
QuickSort(data, key_index+1, end);//递归排序右边
}4. 递归测试代码
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void QuickSort(int* data, int begin, int end)
{
if (begin >= end)
return;//结束条件
int prev = begin;
int cur = begin + 1;
int key_index = begin;
while (cur <= end)
{
if (data[cur] < data[key_index] && ++prev != cur)//如果prev和cur指向同一个数据没必要交换
{
Swap(&data[cur], &data[prev]);
}
++cur;
}
Swap(&data[key_index], &data[prev]);
key_index = prev;//cur越界时,prev的位置
QuickSort(data, begin, key_index-1);//递归排序左边
QuickSort(data, key_index+1, end);//递归排序右边
}
int main()
{
//int a[] = {6,1,2,7,9,3,4,5,10,8 };
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
print(a, sizeof(a) / sizeof(int));
QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
print(a, sizeof(a) / sizeof(int));
return 0;
}(四)非递归实现(栈)

#include<iostream>
#include<algorithm>
#include<stack>
using namespace std;
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
cout << data[i]<<" ";
}
cout << endl;
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
int PartSort(int* data, int begin, int end)
{
int key_index = begin;
int left = begin;
int right = end;
while (left < right)
{
//右边先走
while (left < right && data[right] >= data[key_index])//右边找小
{
--right;
}
while (left < right && data[left] <= data[key_index])//左边找大
{
++left;
}
Swap(&data[left], &data[right]);
}
Swap(&data[key_index], &data[left]);
return left;//返回相遇点,key的当前下标
}
void QuickSort(int* data, int begin, int end)
{
stack<int>s;
s.push(begin);
s.push(end);
while (!s.empty())
{
int right = s.top();
s.pop();
int left = s.top();
s.pop();
int key_index = PartSort(data, left, right);//一趟快排以后key新的下标
//[left,key_index-1] key_index [key_index+1,right]
if (key_index+1 < right)//右区间合理则先入栈
{
s.push(key_index + 1);
s.push(right);
}
if (left < key_index - 1)//左区间入栈
{
s.push(left);
s.push(key_index - 1);
}
}
}
int main()
{
//int a[] = {6,1,2,7,9,3,4,5,10,8 };
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
print(a, sizeof(a) / sizeof(int));
QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
print(a, sizeof(a) / sizeof(int));
return 0;
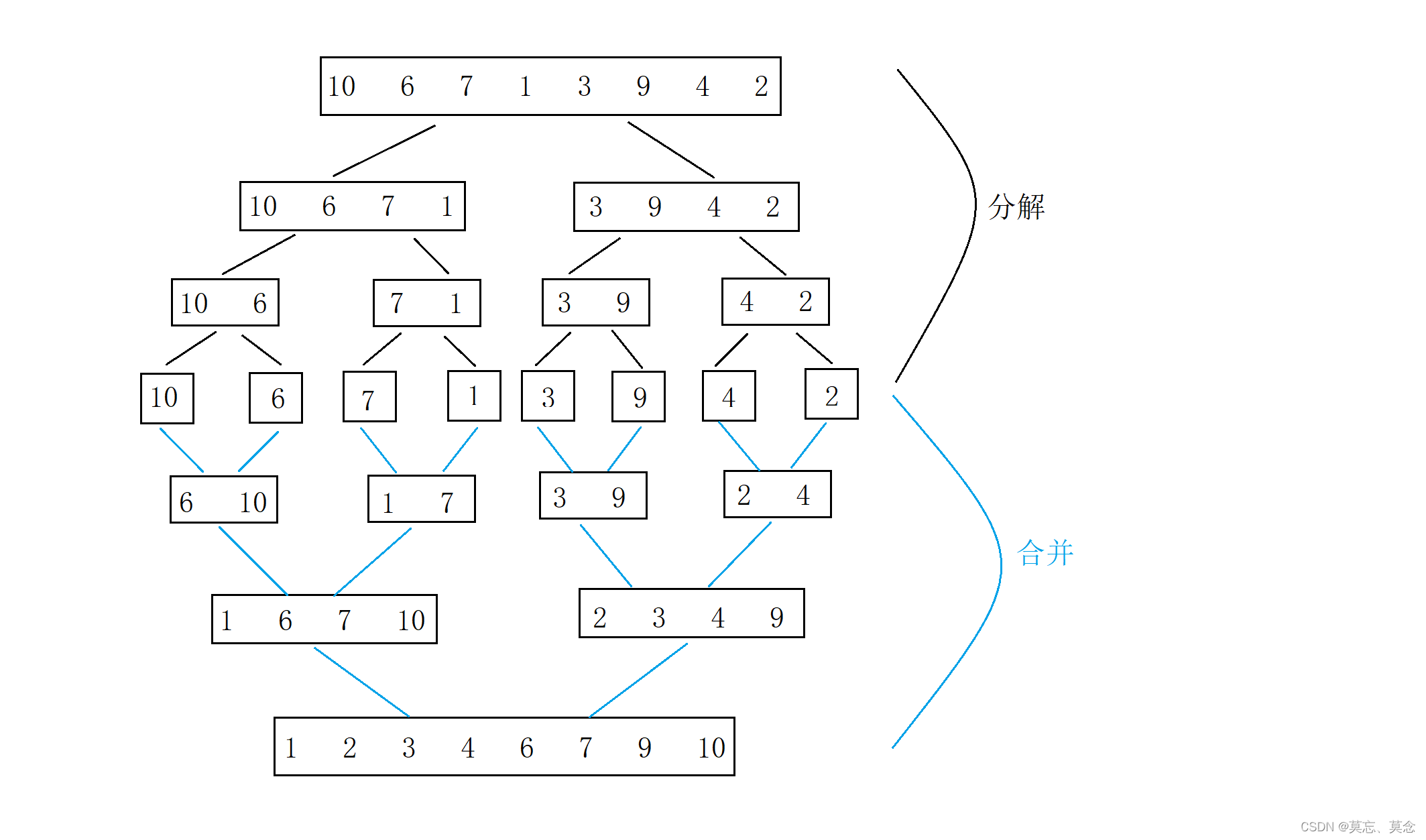
}六、归并排序

1. 递归核心代码
void _MergeSort(int* data, int left, int right, int* tmp)
{
if (left == right)//当只有一个数据的时候不再分解
return;//结束条件
int mid = (left+right)/2;
//[left,mid] [mid+1,right]
_MergeSort(data, left, mid, tmp);
_MergeSort(data, mid + 1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int k = left;//每一个回合都从下标为left位置处在tmp中存放数据
while (begin1 <= end1 && begin2 <= end2)
{
if (data[begin1] <= data[begin2])
{
tmp[k++] = data[begin1++];
}
else
{
tmp[k++] = data[begin2++];
}
}
while (begin1 <= end1)
{
tmp[k++] = data[begin1++];
}
while (begin2 <= end2)
{
tmp[k++] = data[begin2++];
}
memcpy(data + left, tmp + left, sizeof(int) * (right - left+1));
}2. 测试代码
#include<stdio.h>
#include<malloc.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ",data[i]);
}
printf("\n");
}
void _MergeSort(int* data, int left, int right, int* tmp)
{
if (left == right)//当只有一个数据的时候不再分解
return;//结束条件
int mid = (left+right)/2;
//[left,mid] [mid+1,right]
_MergeSort(data, left, mid, tmp);
_MergeSort(data, mid + 1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int k = left;//每一个回合都从下标为left位置处在tmp中存放数据
while (begin1 <= end1 && begin2 <= end2)
{
if (data[begin1] <= data[begin2])
{
tmp[k++] = data[begin1++];
}
else
{
tmp[k++] = data[begin2++];
}
}
while (begin1 <= end1)
{
tmp[k++] = data[begin1++];
}
while (begin2 <= end2)
{
tmp[k++] = data[begin2++];
}
memcpy(data + left, tmp + left, sizeof(int) * (right - left+1));
}
void MergeSort(int* data, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
_MergeSort(data, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
int main()
{
int a[] = {10,6,7,1,3,9,4,2};
print(a, sizeof(a) / sizeof(int));
MergeSort(a, sizeof(a) / sizeof(int) );
print(a, sizeof(a) / sizeof(int));
return 0;
}3. 非递归核心代码

void _MergeSort(int* data, int* tmp,int begin1,int end1,int begin2,int end2)
{
int j = begin1;
int k = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (data[begin1]<=data[begin2])
{
tmp[k++] = data[begin1++];
}
else
{
tmp[k++] = data[begin2++];
}
}
while (begin1 <= end1)
{
tmp[k++] = data[begin1++];
}
while (begin2 <= end2)
{
tmp[k++] = data[begin2++];
}
for (j; j <= end2; j++)//一个一个拷贝
{
data[j] = tmp[j];
}
//等价形式
//memcpy(data+j, tmp+j, sizeof(int) * (end2 - j)+1);//左闭右闭
}
void MergeSort(int* data, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2*gap)//i+2gap是下一组begin1的起始下标
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = begin2 + gap - 1;
if (end1 >= n || begin2 >= n)//最后一组数据的第一个区间的后半部分不存在或者第二个区间整个不存在,都不需要进行合并
{
break;//意味着不需要进行_MergeSort,不用进行合并操作
}
if (end2 >= n)
{
end2 = n - 1;//最后一组数据的第2个区间的后半部分超出了
}
_MergeSort(data, tmp, begin1, end1, begin2, end2);
}
gap = gap * 2;
}
free(tmp);
tmp = NULL;
}4. 测试代码
#include<stdio.h>
#include<malloc.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ",data[i]);
}
printf("\n");
}
void _MergeSort(int* data, int* tmp,int begin1,int end1,int begin2,int end2)
{
int j = begin1;
int k = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (data[begin1]<=data[begin2])
{
tmp[k++] = data[begin1++];
}
else
{
tmp[k++] = data[begin2++];
}
}
while (begin1 <= end1)
{
tmp[k++] = data[begin1++];
}
while (begin2 <= end2)
{
tmp[k++] = data[begin2++];
}
for (j; j <= end2; j++)//一个一个拷贝
{
data[j] = tmp[j];
}
//等价形式
//memcpy(data+j, tmp+j, sizeof(int) * (end2 - j)+1);//左闭右闭
}
void MergeSort(int* data, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2*gap)//i+2gap是下一组begin1的起始下标
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = begin2 + gap - 1;
if (end1 >= n || begin2 >= n)//最后一组数据的第一个区间的后半部分不存在或者第二个区间整个不存在,都不需要进行合并
{
break;//意味着不需要进行_MergeSort,不用进行合并操作
}
if (end2 >= n)
{
end2 = n - 1;//最后一组数据的第2个区间的后半部分超出了
}
_MergeSort(data, tmp, begin1, end1, begin2, end2);
}
gap = gap * 2;
}
free(tmp);
tmp = NULL;
}
int main()
{
int a[] = {10,6,7,1,3,9,4,2,5};
print(a, sizeof(a) / sizeof(int));
MergeSort(a, sizeof(a) / sizeof(int) );
print(a, sizeof(a) / sizeof(int));
return 0;
}七、堆排序
1. 向下调整
void AdjustDown(int* data,int n, int parent)//向下调整
{
int child = 2 * parent + 1;//先假设左孩子结点的值最小
while (child < n)
{
if (child+1<n && data[child+1] < data[child])
{
++child;
}
if (data[child] < data[parent])//排升序
{
Swap(&data[child], &data[parent]);
parent = child;
child = 2 * parent + 1;
}
else//已成堆
break;
}
}2. 建堆
void CreateHeap(int* data, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(data, n, i);
}
}#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void AdjustDown(int* data, int n, int parent)//向下调整
{
int child = 2 * parent + 1;//先假设左孩子结点的值最小
while (child < n)
{
if (child + 1 < n && data[child + 1] < data[child])
{
++child;
}
if (data[child] < data[parent])//排升序
{
Swap(&data[child], &data[parent]);
parent = child;
child = 2 * parent + 1;
}
else//已成堆
break;
}
}
void CreateHeap(int* data, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(data, n, i);
}
}
int main()
{
int a[] = { 2,7,4,6,3,8,1 };
print(a, sizeof(a) / sizeof(int));
CreateHeap(a, sizeof(a) / sizeof(int));
print(a, sizeof(a) / sizeof(int));
return 0;
}3. 堆排序代码
void HeapSort(int* data, int n)
{
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(data, n, i);//建小根堆
}
//排降序
for (int i = 0; i < n; i++)
{
Swap(&data[0], &data[n - 1 - i]);//将堆顶元素和最后一个元素互换,再迭代向下调整
AdjustDown(data, n - 1- i, 0);//n-1-i是重新建堆的数据个数
}
}#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void AdjustDown(int* data, int n, int parent)//向下调整
{
int child = 2 * parent + 1;//先假设左孩子结点的值最小
while (child < n)
{
if (child + 1 < n && data[child + 1] < data[child])
{
++child;
}
if (data[child] < data[parent])//排升序
{
Swap(&data[child], &data[parent]);
parent = child;
child = 2 * parent + 1;
}
else//已成堆
break;
}
}
void HeapSort(int* data, int n)
{
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(data, n, i);//建小根堆
}
//调整
for (int i = 0; i < n; i++)
{
Swap(&data[0], &data[n - 1 - i]);//将堆顶元素和最后一个元素互换,再迭代向下调整
AdjustDown(data, n - 1- i, 0);//n-1-i是重新建堆的数据个数
}
}
int main()
{
int a[] = { 2,7,4,6,3,8,1 };
print(a, sizeof(a) / sizeof(int));
HeapSort(a, sizeof(a) / sizeof(int));
print(a, sizeof(a) / sizeof(int));
return 0;
}4. 向上调整
void AdjustUp(int* data, int n, int child)//向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (data[child] < data[parent])
{
Swap(&data[child], &data[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}5. 测试
#include<stdio.h>
void print(int* data, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
printf("\n");
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void AdjustUp(int* data, int n, int child)//向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (data[child] < data[parent])
{
Swap(&data[child], &data[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
void CreateHeap(int* data, int n)
{
//建堆
for (int i = n - 1; i >= 0; --i)
{
AdjustUp(data, n, i);//建小根堆
}
}
int main()
{
int a[] = { 2,7,4,6,3,8,1 };
print(a, sizeof(a) / sizeof(int));
CreateHeap(a, sizeof(a) / sizeof(int));
print(a, sizeof(a) / sizeof(int));
return 0;
}