文章目录
- 🍀二叉树的存储
- 🌳二叉树的基本操作
- 🐱👤二叉树的创建
- 🐱👓二叉树的遍历
- 🎡前中后序遍历
- 📌前序遍历
- 📌中序遍历
- 📌后续遍历
- 🛫层序遍历
- 🐱👤前中后序代码实现(递归)
- 🚩前序遍历
- 🚩中序遍历
- 🚩后续遍历
- 🛬前中后序练习题
- 🐱🏍二叉树的基本操作
- 🎈获取树中节点的个数
- 🎈获取叶子节点的个数
- 🎈获取第K层节点的个数
- 🎈 获取二叉树的高度
- 🎈检测值为value的元素是否存在
- ⭕总结

🍀二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储
这里博主讲一下链式存储
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式
二叉表示:
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
三叉表示:
/
/ 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}
这里博主主要讲解一下孩子表示法
🌳二叉树的基本操作
🐱👤二叉树的创建
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树。
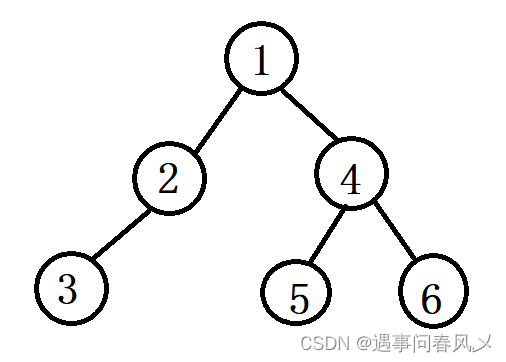
创建如下:
public class BinaryTree{
public static class BTNode{
BTNode left;
BTNode right;
int value;
BTNode(int value){
this.value = value;
}
}
private BTNode root;
public void createBinaryTree(){
BTNode node1 = new BTNode(1);
BTNode node2 = new BTNode(2);
BTNode node3 = new BTNode(3);
BTNode node4 = new BTNode(4);
BTNode node5 = new BTNode(5);
BTNode node6 = new BTNode(6);
root = node1;
node1.left = node2;
node2.left = node3;
node1.right = node4;
node4.left = node5;
node5.right = node6;
}
}
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解
在我们对二叉树进行基本操作之前,我们的先来回顾以下二叉树
二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的
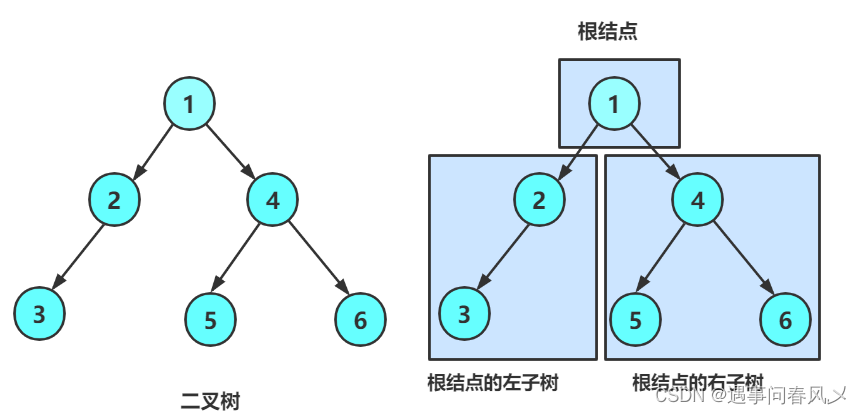
从概念中可以看出,二叉树的每一个子树又是一个新的二叉树,所以可以知道二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
🐱👓二叉树的遍历
🎡前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1) 。
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的
左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
-
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
-
LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
-
LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点
📌前序遍历
前序遍历(Preorder Traversal 亦称先序遍历)规则为
访问根结点—>根的左子树—>根的右子树
比如以下二叉树:
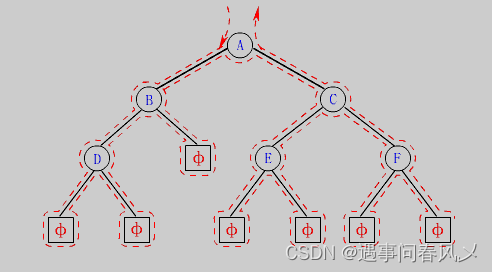
前序遍历的顺序为:
1.== 遍历A结点==
2. 遍历A结点的左子树
3. 遍历B结点
4. 遍历B结点的左子树
5. 遍历D结点
6. 判断D的左右子树为空后返回
7. 遍历B结点的右子树,为空返回
8. 此时A结点左子树遍历完,开始遍历A结点右子树
9. 遍历C结点
10.遍历C结点的左子树
11.遍历E结点
12.判断E结点的左右子树为空后返回
13.遍历C结点的右子树
14.遍历F结点
15.判断F结点的左右子树为空后返回
16.自此遍历完毕全部返回
最后前序的遍历结果为:
A->B->D->C->E->F
📌中序遍历
中序遍历(Inorder Traversal)的访问规则为:
根的左子树—>根节点—>根的右子树。
比如以下二叉树:

中序遍历的顺序为:
- 遍历A结点的左子树
- 遍历B结点的左子树
- 遍历D结点的左子树,发现为空返回
- 遍历D结点
- 遍历D结点的右子树,发现为空返回
- 遍历B结点
- 遍历B结点的右子树。发现为空返回
- 此时左子树遍历完成
- 遍历A结点
- 遍历A结点右子树
- 遍历C结点左子树
- 遍历E结点的左子树,发现为空返回
- 遍历E结点
- 遍历E结点的右子树,发现为空返回
- 遍历C结点
- 遍历C结点的左子树
- 遍历F结点的左子树,发现为空返回
- 遍历F结点
- 遍历F结点的右子树,发现为空返回
- 自此遍历完毕全部返回
最后中序的遍历结果为:
D->B->A->E->C->F
📌后续遍历
后序遍历(Postorder Traversal)的访问规则为:
根的左子树—>根的右子树—>根节点
比如以下二叉树:

后续遍历的顺序为:
- 遍历A结点的左子树
- 遍历B结点的左子树
- 遍历D结点的左子树,为空后返回
- 遍历D结点的右子树,为空后返回
- 遍历D结点
- 遍历B结点的右子树,为空后返回
- 遍历B结点
- 遍历A结点的右子树
- 遍历C结点的左子树
- 遍历E结点的左子树,为空后返回
- 遍历E结点的右子树,为空后返回
- 遍历E结点
- 遍历C结点的右子树
- 遍历F结点的左子树,为空后返回
- 遍历F结点的右子树,为空后返回
- 遍历F结点
- 遍历C结点
- 遍历A结点
- 至此遍历完毕,全部返回
最后后序的遍历结果为:
D->B->E->F->C->A
🛫层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
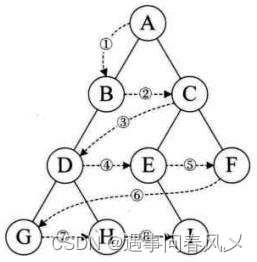
🐱👤前中后序代码实现(递归)
我们发现二叉树本质上是一个个小二叉树组成的
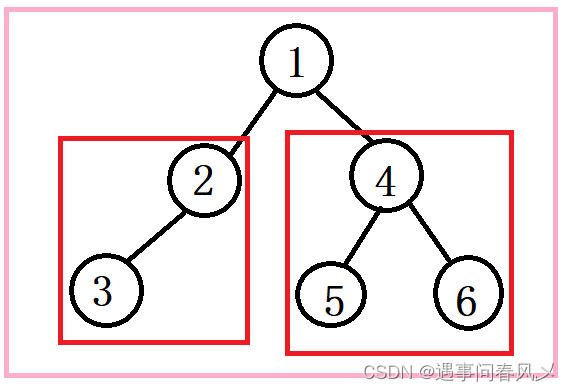
那我们递归不就是把大事化小,复杂变简单吗?
因此我们就可以利用递归的思想进行实现
我们二叉树看成最简单的,也就下面几种情况
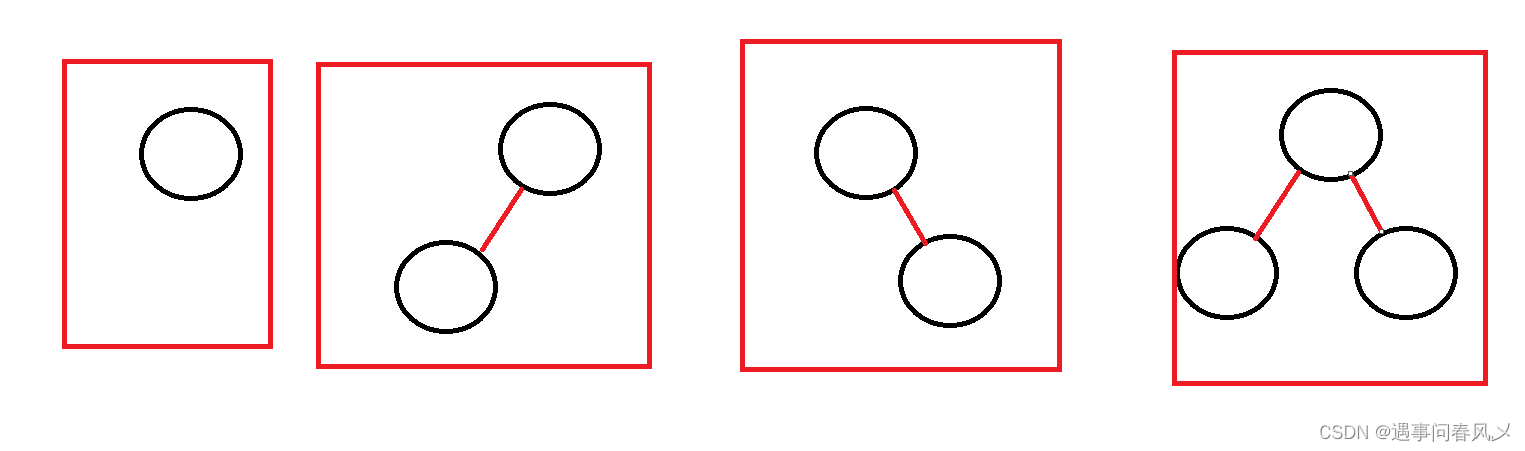
我们从根节点开始遍历,遇到空然后返回打印当前结点就好
🚩前序遍历
// 前序遍历 根 左子树 右子树 递归
public void preOrder(TreeNode root) {
if(root == null) {
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}
🚩中序遍历
// 中序遍历
public void inOrder(TreeNode root) {
if(root == null) {
return;
}
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}
🚩后续遍历
// 后序遍历
public void postOrder(TreeNode root) {
if(root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+" ");
}
🛬前中后序练习题
-
某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A)
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA -
二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为(A)
A: E B: F C: G D: H -
设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为(D)
A: adbce B: decab C: debac D: abcde -
某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为(A)
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
总结:给出前序遍历与中序遍历和给出后序遍历与中序遍历可以确定一个二叉树,但是不给中序遍历或者只给一个中序遍历,是无法确定一个二叉树的
🐱🏍二叉树的基本操作
🎈获取树中节点的个数
依旧利用递归的思想,遍历每一棵小树,若当前结点为空,返回0
先获取左节点个数,再获取右节点个数
然后返回两者相加再加上根节点的个数1
比如以下结点:
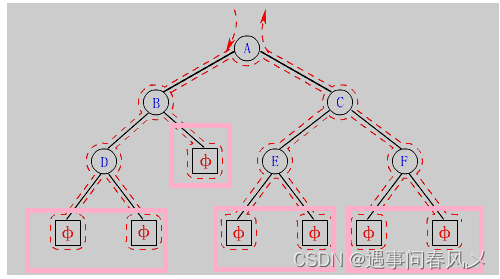
若当前结点不为空,则返回1;
代码实现如下:
public int size(BTNode root) {
if (root == null) {
return 0;
}
int leftSize = size(root.left);
int rightSize = size(root.right);
return leftSize + rightSize + 1;
}
🎈获取叶子节点的个数
依旧利用递归的思想,遍历每一棵小树,若当前结点为空,返回0
当前节点的左右子树若都为空,说明该节点为叶子结点,返回1
先获取左节点个数,再获取右节点个数
然后两者相加
代码实现如下:
int getLeafNodeCount(BTNode root) {
if(root == null) {
return 0;
}
if(root.left == null && root.right == null){
return 1;
}
int leftSize = getLeafNodeCount(root.left);
int rightSize = getLeafNodeCount(root.right);
return leftSize+rightSize;
}
🎈获取第K层节点的个数
依旧利用递归的思想,每进去一次,K-1,当k=1时,此时若该节点不为空则返回1
为空则返回0
先遍历左子树k层结点,再遍历右子树k层结点
最后左子树结点加上右子树结点,就是该层结点总数
int getKLevelNodeCount(TreeNode root,int k) {
if(root == null) {
return 0;
}
if(k == 1) {
return 1;
}
int leftSize = getKLevelNodeCount(root.left,k-1);
int rightSize = getKLevelNodeCount(root.right,k-1);
return leftSize+rightSize;
}
🎈 获取二叉树的高度
分别统计左右子树的高度,然后进行比较
返回高度高的子树并加上根节点
public int maxDepth(BTNode root) {
if(root == null) {
return 0;
}
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return (leftHeight > rightHeight) ?
(leftHeight+1):(rightHeight+1);
}
🎈检测值为value的元素是否存在
依旧利用递归的思想
先遍历左子树,若没有找到,则返回null
若返回不为null,则返回该结点
若左子树没有,则遍历右子树,道理相同
若最后都没找到,则返回null;
BTNode find(BTNode root, int val) {
if (root == null) {
return null;
}
if (root.val == val) {
return root;
}
BTNode leftTree = find(root.left, val);
if (leftTree != null) {
return leftTree;
}
BTNode rightTree = find(root.right, val);
if (rightTree != null) {
return rightTree;
}
return null;//没有找到
}
⭕总结
关于《【数据结构】二叉数的存储与基本操作的实现》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!