算法基础第三章
- 1、dfs(深度搜索)
- 1.1、 递归+回溯
- 1.2、递归+剪枝(剪枝就是判断接下来的递归都不会满足条件,直接回溯,不再继续往下无意义的递归)
- 2、bfs(广度搜索)
- 2.1、最优路径(只适合于边权都相等的题)
- 3、邻接表存储树和图(邻接表就是单链表 )
- 3.1、深度优先遍历(特殊的深搜)
- 3.2、宽度优先遍历(特殊的宽搜)
- 3.3、有向图的拓扑序列(有环的有向图不可能是拓扑序列)
- 4、最短路
- 4.1、单源最短路
- 4.1.1、所有边权都是整数
- 4.1.2、存在负权边
- 4.2、多源汇最短路
- 5、最小生成树
- 5.1、prim算法
- 5.2、Kruskal算法(稀疏图)
- 6、二分图
- 6.1、染色法
- 6.2、匈牙利算法
1、dfs(深度搜索)
1.1、 递归+回溯
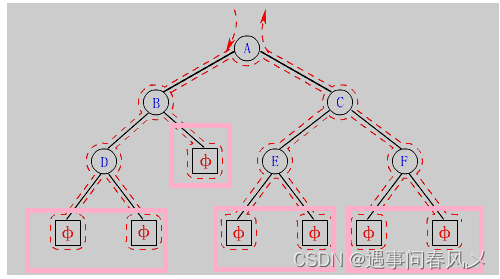
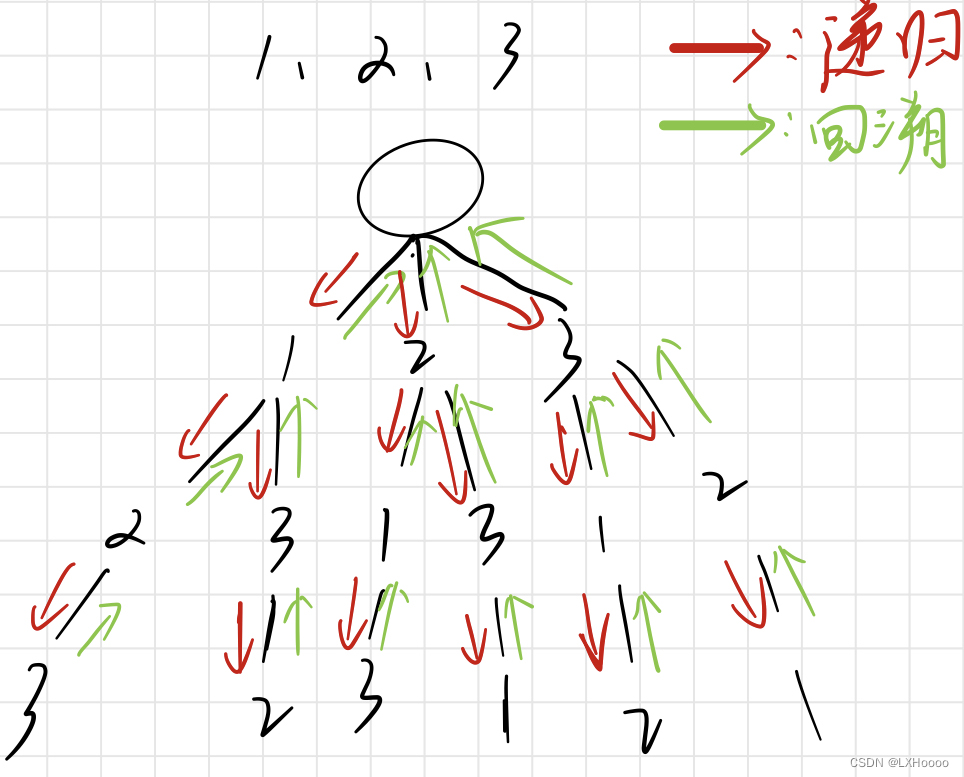
- 解析:下图为1,2,3三个数的全排列过程,从0层开始,一直往下递归,直到数的个数用完,每次使用了一个数需要将这个数标记为已使用过,回溯的时候再恢复为未使用过。
- 题目链接:一个数的全排列
- 代码
#include <iostream>
#include<stdio.h>//加了这个头文件时间快了1ms
using namespace std;
const int N = 7;
bool use[N];//这个数被用过的话则记为true,排列的时候位置上只能放没被用过的
int path[N],n;
void dfs(int num)
{
if(num == n)//输入3,怎有3个空位排列,填满之后就输出
{
for(int i = 0; i < n; i++)
{
printf("%d ",path[i]);
}
puts("");
return;
}
for(int i = 1; i <= n; i++)
{
if(!use[i])
{
path[num] = i;
use[i] = true;
dfs(num + 1);
use[i] = false;
}
}
}
int main() {
cin >> n;
dfs(0);//从0开始
return 0;
}
1.2、递归+剪枝(剪枝就是判断接下来的递归都不会满足条件,直接回溯,不再继续往下无意义的递归)
- 解析:
- 题目链接:n皇后问题
- 代码:代码并没有全a,路过的大佬可以给个补充
#include <iostream>
using namespace std;
const int N = 20;
int n;
bool col[N],dg[N],udg[N];
long long ret;
void dfs(int num)
{
if(num == n)
{
ret++;
return;
}
for(int i = 0; i < n; i++)
{
if(!col[i] && !dg[i+num] && !udg[n-num+i])
{
col[i] = dg[i+num] = udg[n-num+i] = true;
dfs(num+1);
col[i] = dg[i+num] = udg[i-num+n] = false;
}
}
}
int main() {
scanf("%d",&n);
dfs(0);
printf("%lld",ret);
}
2、bfs(广度搜索)
//基本框架,伪代码
queue_init;
while(!queue.empty())
{
t = queue.pop();//弹出队头元素
queue.push(t.child->node);//这里包括左右子节点
}
2.1、最优路径(只适合于边权都相等的题)
- 解析:
- 题目链接:走迷宫
- 代码
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef pair<int,int> PII;
const int N = 1010;
char g[N][N];//存储地图数据
int d[N][N];//存储距离
int n,m,posx1,posy1,posx2,posy2;//传入的行和列数以及起始终止点的位置
PII q[N*N];//数组模拟队列,需要开元素的个数的大小
int bfs(int posx2,int posy2)
{
int hh=0,tt=0;//队头和队尾指针
q[0] = {posx1-1,posy1-1};//队列初始化,放入起始位置的坐标
memset(d,-1,sizeof d);//d初始化为-1,-1表示这个位置还未经过,sizeof(d) = N*N*4,int是个字节,所以乘4
d[posx1-1][posy1-1] = 0;//起始位置与自己的距离是0
int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};//四个方向的移动x和y的坐标的变化
while(hh <= tt)//队列非空
{
auto t = q[hh++];//弹出队头元素
for(int i = 0; i < 4; i++)//四个方向的移动
{
int x = t.first + dx[i],y = t.second + dy[i];
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == '.' && d[x][y] == -1)//这个点未走过且在边界内且无障碍物
{
d[x][y] = d[t.first][t.second] + 1;//这个点与起始位置的点的距离在上一个点的距离上加1
q[++tt] = {x,y};//从队尾压入新的位置的坐标
}
if(d[posx2-1][posy2-1] != -1)//表示到达终止点,返回
{
return d[posx2-1][posy2-1];
}
}
}
return -1;
}
int main()
{
scanf("%d%d%d%d%d%d",&n,&m,&posx1,&posy1,&posx2,&posy2);
getchar();
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
scanf("%c",&g[i][j]);
}
getchar();//读取换行符
}
printf("%d",bfs(posx2,posy2));
return 0;
}
3、邻接表存储树和图(邻接表就是单链表 )
- 树是特殊的有向图,是无环连通图
- 无向图也是一种特殊的有向图,是双向的
- 邻接表的存储代码
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010,M = N*2;
int h[N],e[M],ne[M],idx;
/* a:被插入的节点
* b:新插入的节点,之后有a指向b的边
*/
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a],h[a] = idx++;
}
int main()
{
memset(h,-1,sizeof h);//h数组是图里面的节点,初始都是指向-1,也就是相当于nullptr
}
3.1、深度优先遍历(特殊的深搜)
- 解析:有向图的遍历,深度遍历,逮住一个起点一直往下递归,每个点只遍历一次,直到结束再回溯再递归,一直遍历完所有的点
- 题目链接:未找到对应的题目,贴上acwing原题
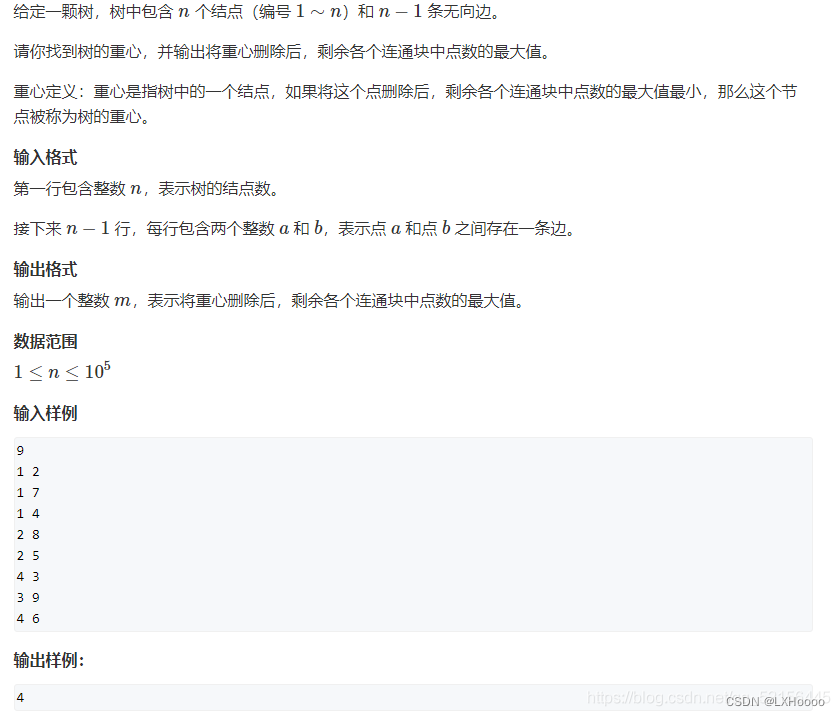
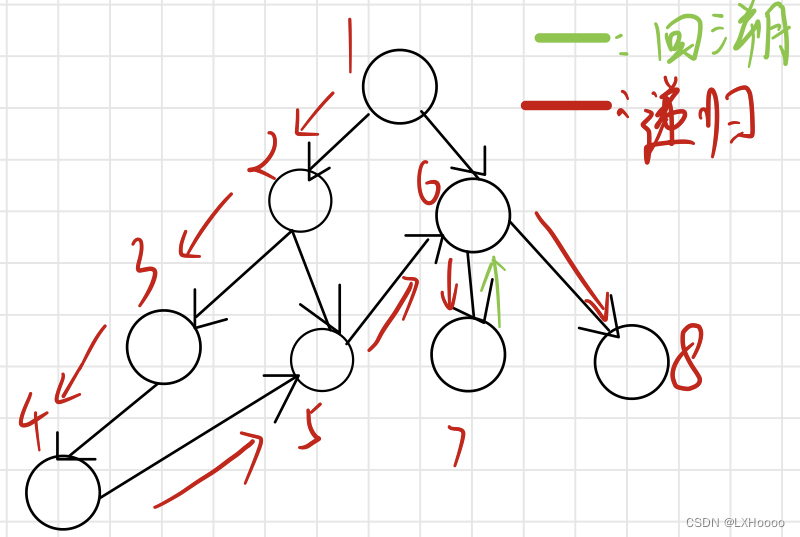
- 题目解析:图中的无向图,可以看到左图删除节点1,有三个连通域,大小分别是3,4,1,最大值为4,我们只需要遍历节点1 的子节点就能得到三个大小。右图删除节点4,三个连通域大小分别为5,2,1,上面连通域的大小我们只要求出节点4的子节点数,用总数减去就能得到。那对应的每删除一个节点都有相应的连通域,要求出这些连通域中最大值中的最小值。
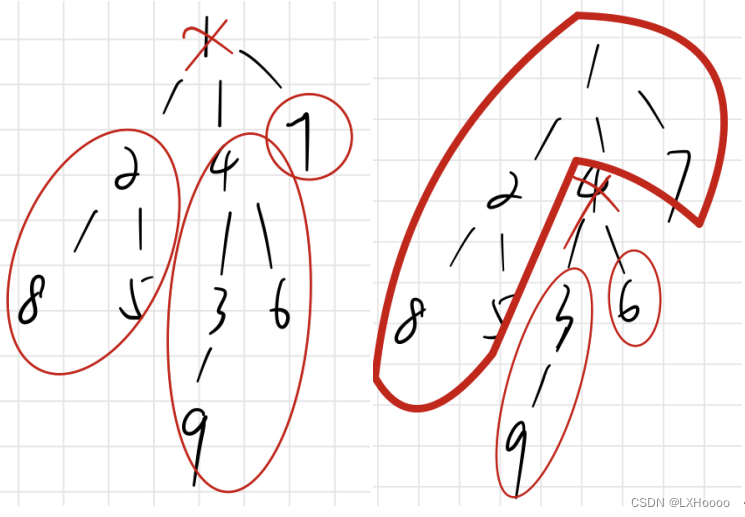
- 代码解析:下面的代码初看是有点绕的,图中举了一个较短的例子遍历,可以先把数组的内容全都列出来,假设从1节点开始:1)dfs(1),i=h[1]=2,j=e[2]=3;2)dfs(3),i=h[3]=3,j=e[3]=1,continue;3)i=ne[3]=-1;4)i=ne[2]=0,j=e[0]=2;5)dfs(2),i=h[2]=6,j=e[6]=5;6)dfs(5),i=h[5]=7,j=e[7]=2,continue;7)i=ne[7]=-1;8)i=ne[6]=4,j=e[4]=4;9)dfs(4),i=h[4]=5,j=e[5]=2,continue;10)i=ne[5]=-1;11)i=ne[4]=1,j=e[1]=1,continue;12)i=ne[1]=-1结束。遍历的顺序是1->3->-1再返回1,接着1->2->5->-1再返回2,接着2->4->-1再返回2,2再返回1,1->-1结束遍历。可以看到3的ne保存这到2路径,也就是直接从1到2,中间省去了1。
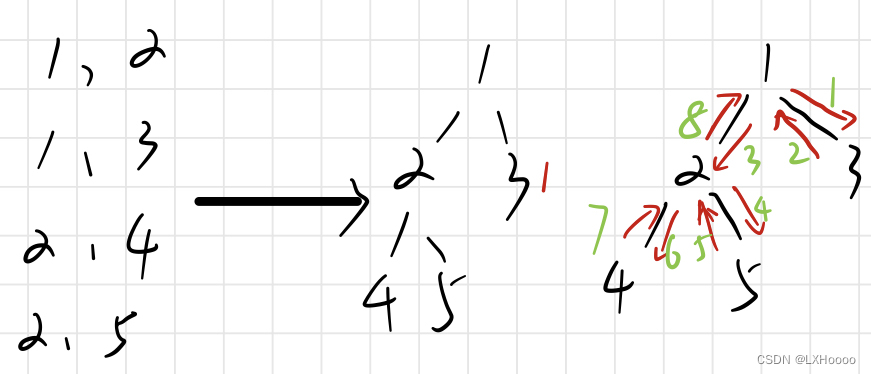
- 代码(acwing源码)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = N * 2;//因为需要建立两份边,所以 M = 2 * N;
int n;
int h[N], e[M], ne[M], idx;
int ans = N;
bool st[N];
//添加边的模板,要求熟练的默写,这部分的解释在 链表 专题中
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
//返回以u为根的子树中节点的个数,包括u节点
int dfs(int u)
{
st[u] = true;
int size = 0, sum = 0;//size存储的是以u为根的数的一个子儿子的节点数的最大值
//sun存储以u为根的树的节点数, 包括u
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (st[j]) continue;
int s = dfs(j); //s存储的就是以 j 为根的子树的节点数,包括 j
size = max(size, s); //每次找出最大的子图的节点数
sum += s; //以j为根的树的节点数
}
size = max(size, n - sum - 1); //求 dfs 遍历的所有子树中最大的节点数的个数和 dfs 未遍历的那棵树的节点数的最大值
ans = min(ans, size);
return sum + 1; //这里返回的个数加上根节点
}
int main()
{
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a); //处理无向图的添边方式
}
dfs(1); //可以选择任意一个点开始进行 dfs,又u <= n,且 n 的最小值为1,所以只能从 1 开始
//当然本题数据是从 5 开始的,所以对于本题写 dfs (1 ~ 5)均可AC
printf("%d\n", ans);
return 0;
}
3.2、宽度优先遍历(特殊的宽搜)
- 解析:套用宽度优先搜索的模板,逮住一个点开始,遍历所有的节点,看保存的节点个数是否和输入的相等,相等的话则是全连通的,否则不是
- 题目链接:宽度优先遍历
- 代码
#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010,M = N * 2;//因为无向图需要建立两份边,所以 M = 2 * N;
int e[M],ne[M],h[N];
int n,m,idx;
int bfs()//广度优先遍历
{
int hh=0,tt=0;//队头和队尾指针
int q[N];//数组模拟队列
bool st[N];//是否遍历过标记
q[0] = 1;//队列初始化,模板步骤
st[1] = true;//这个元素被遍历过了
int ret = 0;//保存节点数
while(hh <= tt)//队列不为空
{
int t = q[hh++];//弹出队头
for(int i = h[t]; i != -1; i = ne[i])//按照边去遍历
{
int j = e[i];
if(st[j])
continue;
else
st[j] = true,ret++,q[++tt] = j;//该节点未被遍历过,则压进队尾,标记被遍历,节点数加1
}
}
return ret+1;//因为开始的节点本身没被算进去,需要加1
}
void add(int x,int y)//无向图的建立,前面已经解释过了
{
e[idx] = y,ne[idx] = h[x],h[x] = idx++;
}
int main() {
memset(h,-1,sizeof h);
while(cin >> n >> m)
{
if(!n && !m)
break;
while(m--)
{
int x,y;
cin >> x >> y;
add(x,y),add(y,x);//建立双边
}
if(bfs()==n)
{
cout << "YES" << endl;
memset(h,-1,sizeof h);//因为输入是有很多图的,处理完一个无序图需要重新清空准备处理下一个无序图
memset(e,0,sizeof e);
memset(ne,0,sizeof ne);
idx = 0;
}
else
{
cout << "NO" << endl;
memset(h,-1,sizeof h);
memset(e,0,sizeof e);
memset(ne,0,sizeof ne);
idx = 0;
}
}
}
3.3、有向图的拓扑序列(有环的有向图不可能是拓扑序列)
- 入度:一个点有多少指向自己的边
- 出度:一个点有多少边从自己这出去
- 解析:当一个图按拓扑序排好之后,起点一定是在终点的前面,如图中所示,当按1,2,3排序就是一个拓扑序列,所有边的起点都在终点的前面。当求解一个有向图是否能够组成拓扑排序的时候,也就是看看能否将所有的节点的入度都处理为0,能的话就能拓扑排序,否则就不能

- 题目连接:拓扑排序
- 代码
#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 200010;
int e[N],ne[N],h[N];
int d[N];
int n,m,idx;
int q[N];//宽搜的模板队列
void add(int x,int y)//图的构建
{
e[idx] = y,ne[idx] = h[x],h[x] = idx++;
}
bool tuposort()//拓扑排序
{
int hh = 0,tt = -1;
for(int i =1; i <= n; i++)
{
if(!d[i])
q[++tt] = i;//首先把所有入度为0的点压入队列
}
while(hh <= tt)//宽搜模板
{
int t = q[hh++];//弹出队头,元素还在数组里面,只是用了头尾指针来表示弹出与压入
for(int i = h[t]; i != -1; i = ne[i])//宽搜遍历,这个是有向图,不会重复遍历
{
int j = e[i];
d[j]--;//该节点的入度减1
if(d[j] == 0)
q[++tt] = j;//该节点入度变为0之后就压入队列
}
}
return tt == n-1;//所有的点都能够被入队说明是一个有向无环图,即能构成拓扑排序
}
int main() {
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
while(m--)
{
int x,y;
cin >> x >> y;
add(x,y);
d[y]++;//保存这个点的入度
}
if(tuposort())
{
for(int i = 0; i < n; i++)
{
if(i!=n-1)
printf("%d ",q[i]);
else
printf("%d",q[i]);//答案最后有一个数不能有空格,有空格提交不成功
}
}
else {
printf("%d",-1);//无拓扑排序输出-1
}
}
4、最短路
4.1、单源最短路
- 求一个点到其他所有点的最短路
4.1.1、所有边权都是整数
- 朴素Dijkstra:稠密图(邻接矩阵),m(边数)~n^2(点数)
- 模板:
- 1.dist[1] = 0,dist[i] = 正无穷
- 2.for i 1~n(迭代)
- t<-不在s中的,距离最近的点
- s<-t;//s是当前已确定最短距离的点
- 用t更新其他点的距离
- 题目链接:Dijkstra求最短路径
- 代码
- 模板:
class Solution {
public:
int networkDelayTime(vector<vector<int>> ×, int n, int k) {
const int inf = INT_MAX/2;
//构建邻接矩阵
int g[n][n];
memset(g,0x3f3f3f3f,sizeof g);//这里初始化后的值不等于inf
for(auto &t:times)
{
int x = t[0]-1,y = t[1]-1;
g[x][y] = min(g[x][y],t[2]);
}
-
- //存储距离的数组,初始化为g数组一样的最大值
vector<int>dist(n,0x3f3f3f3f);//保存距离
dist[k-1] = 0;//k是出发点,将出发点的距离设为0,数组中的坐标与节点值是-1的关系
vector<int> st(n,0);//保存是否遍历过的标记
for(int i = 0; i < n;i++)//这个循环是遍历n个节点
{
int t = -1;
for(int j = 0; j < n; j++)//这个循环是找到出发点
{
if(!st[j] && (t == -1 || dist[j] < dist[t]))
{
t = j;
}
}
st[t] = true;//标记这个点被遍历了
for(int j = 0; j < n; j++)//这个循环是计算出出发点最到他点的最短距离
{
dist[j] = min(dist[j],dist[t] + g[t][j]);
}
}
int ans = *max_element(dist.begin(),dist.end());
return ans == 0x3f3f3f3f ? -1 : ans;
}
};
- 堆优化版的Dijkstra算法:稀疏图(邻接表),m(边数)~n(点数)
- 解析:堆优化版的改进是在朴素版的基础上,在for循环找到目标最近点用堆来替代,从而减小时间复杂度,题意中可以看到n和m的数量级是相等的,因此是稀疏图,用邻接表来做
- 题目链接:未找到,acwing原题
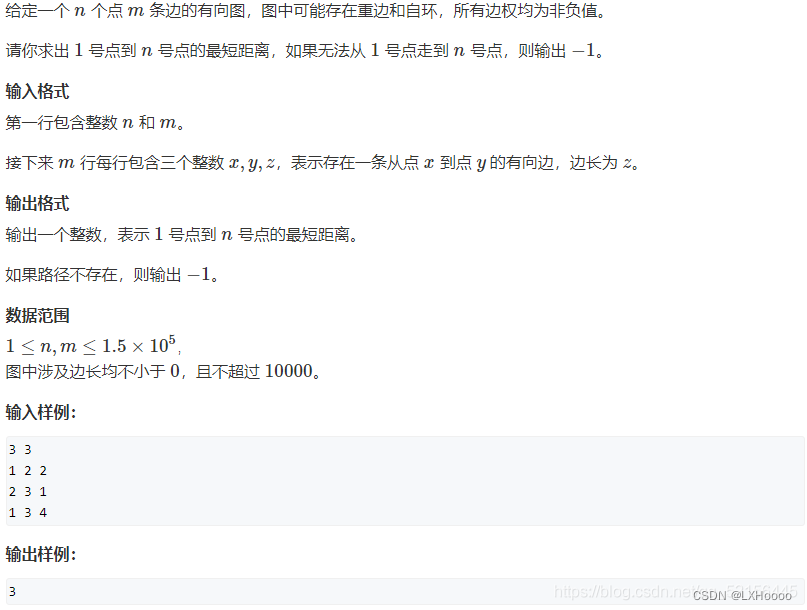
- 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include<vector>
#include<queue>
using namespace std;
typedef pair<int,int>PII;
const int N = 1e6+10;
int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}
int dijkstra()
{
memset(dist,0x3f,sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;//优先队列定义一个小根堆
heap.push({0,1});//整个代码就是邻接表加宽搜模板,初始化队列
while(heap.size())
{
auto t = heap.top();//取出队头
heap.pop();//弹出队头
int ver = t.second,distance = t.first;
if(st[ver])continue;//是否已经遍历过
for(int i = h[ver]; i != -1; i = ne[i])//最短路径替换
{
int j = e[i];
if(dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j],j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);//添加有向边
}
printf("%d\n",dijkstra());
return 0;
}
4.1.2、存在负权边
- Bellman-Ford算法
- 模板
- for n 次
- for 所有边a,b,w
- dist[b] = min(dist[b],dist[a]+w)
- for 所有边a,b,w
- for n 次
- 题目链接:bellman-ford模板算法
- 代码
- 模板
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
int m = flights.size();//写成int m = flights.size()+10; int dist[m],backup[m];会报错
int dist[m+10],backup[m+10];//为了防止超出数组界限,所以在长度上加10
memset(dist,0x3f,sizeof dist);
dist[src] = 0;//从哪个点开始,那个点起始的距离为0
for(int i = 0; i < k+1; i++)//这里k是中转站点,而不是边数,所以是k+1,因为得加上起点
{
memcpy(backup,dist,sizeof dist);//加备份,防止出现串联
for(int j = 0; j < m; j++)
{
auto t = flights[j];
dist[t[1]] = min(dist[t[1]],backup[t[0]] + t[2]);//防止串联,因为要满足k的限制,所以必须保证不能用这次的更新去更新后面的距离
}
}
if(dist[dst] > 0x3f3f3f3f/2) return -1;
else return dist[dst];
}
};
- SPFA算法
- 使用宽搜的队列对Dellman-Ford算法的改进
- 使用SPFA判断负环,也能用于Dijkstra算法解决的最短路径问题
- 题目链接:判断负环
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 210,M = 2010;
int n,m,a,b,c;
int h[N],e[M],ne[M],w[M],idx;
int dist[N],cnt[N];
bool st[N];
//使用邻接表构建图
void add(int a,int b,int c)
{
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}
bool spfa()
{
queue<int>q;
memset(dist,0x3f,sizeof dist);
dist[1] = 0;//因为能到达的话是输出从1号点到n号点的距离,所以1号点的距离初始化为0
for(int i = 1; i <= n; i++)
{
st[i] = true;
q.push(i);//先把所有的点入队列
}
while(q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])//这个条件保证了是负边环
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n) return true;//cnt里面存的是边数,如果边数大等于n,那么点数大等于n+1,因为只有n个点,所以一定是有环的
if(!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
int main() {
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
if(spfa())
puts("circle");
else
{
if(dist[n] == 0x3f3f3f3f)
puts("can't arrive!");
else
cout << dist[n];
}
}
4.2、多源汇最短路
- 源:起点;汇:终点
- 任选两个点,求这两个点之间的最短路
- Floyd算法
- 模板,用邻接矩阵存储边
- d[i,j]
- for(k=1;k<=n;k++)
- for(i=1; i<=m; i++)
- for(j=1; j<=n; j++)
- d[i,j] = min(d[i,j],d[i,j] + d[k,j]);//使用了动态规划的原理
- for(j=1; j<=n; j++)
- for(i=1; i<=m; i++)
- for(k=1;k<=n;k++)
- d[i,j]
- 题目链接:Floyd算法
- 代码
- 模板,用邻接矩阵存储边
在这里插入代码片
5、最小生成树
5.1、prim算法
-
朴素版:稠密图
- 模板
- dist[i]<-inf
- for(i=0;i<n;i++)
- t<-找到集合外距离最近的点
- 用t更新其他点到集合的距离
- st[t] = true;
- 模板
-
解析:起始每个点存储的距离初始化都是inf,随后随便找到一个点开始,图中从1开始,用1到其他点的距离去更新各个点存储的距离,然后1被放入集合
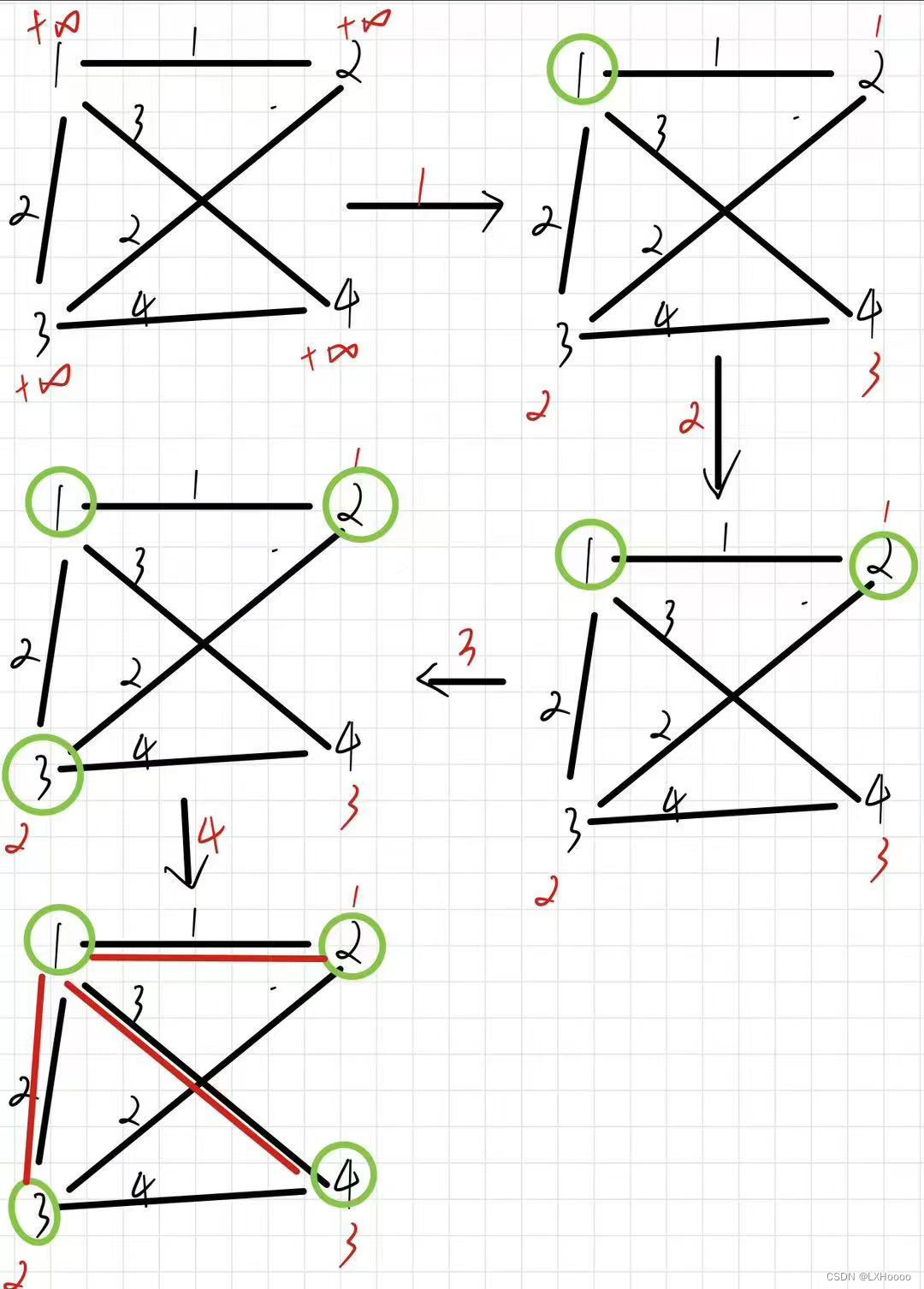
-
堆优化版(一般不用)