用ceres实现lio-sam角点匹配

news2024/11/18 9:44:21

文章开始先扯一堆废话，lio-sam作者手推平面点和角点匹配，对于初学者，尤其数学不好者学习有一定难度，对于工程落地和后期优化而言难度较大。本文基于主流优化库实现角点匹配，以下内容均为原创和作者实测干货（ps:作者有着N年slam工作经验）
补充：作者不善于排版，但内容均为干货
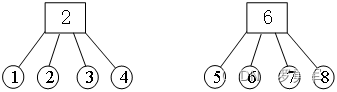
文章开头首先介绍下什么是lio-sam中的角点，千言万语不如直接上图直观
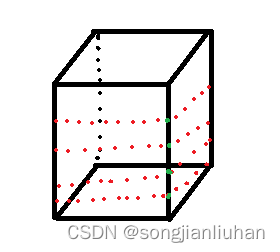
在这里插入图片描述
如上图对于一个立方体物体，多线激光雷达打在该立方体上的点云如上述红色和绿色点云。
图中绿色的点为角点
什么意思呢？就是激光雷达的点云在物体的棱角上的点就是角点，红色的点为平面点

干货来了类似于pl-icp，角点匹配为点到线的距离
首先
点代表 当前激光雷达帧中提取出来的角点
线代表 图中绿色点构成的棱角线

以上为开篇点题，网上有很多大佬介绍算法的，本文指在用ceres实现匹配，替代手推公式匹配。废话不多说上代码。

使用ceres记住一句话就可以，我的残差是个啥？****
交点匹配的目的是让当前激光雷达帧中提取出来的角点到所对应角点构成线的距离最小
残差就是这个距离，距离最小也就是解最小二乘问题

首先先把头文件干上

#include <memory>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Eigen/Core"
#include "ceres/ceres.h"
#include "ceres/jet.h"
#include "ceres/rotation.h"
#include <pcl/point_cloud.h>
#include <pcl/point_types.h>
#include <pcl/kdtree/kdtree_flann.h>

角点残差，代码一多就容易晕乎哈，所有文字解释均在代码中

//角点残差
class CornerPointsCostFunctor{
public:
    //scaling_factor表示权重，简单理解就是比如我这个点的擦差是1，如果权重是2,乘以残差就表示把我这个残差放大，也就是说我更加相信这个点，优化的时候我就要使劲优化它
    //source_cloud表示当前帧中的角点点云
    //target_cloud表示我的local map中的角点点云
    CornerPointsCostFunctor(const double scaling_factor, const pcl::PointCloud<PointType>::ConstPtr source_cloud, 
    const pcl::PointCloud<PointType>::ConstPtr target_cloud/*注意目标角点个数不能小于5个*/) 
    : scaling_factor_(scaling_factor), source_cloud_(source_cloud), target_cloud_(target_cloud){ 
        //构建target_cloud kd_tree, 把localmap创建为kd-tree，目的先透露一下，为了找线，就要搜索对应角点，为了减少搜索的计算量
        kdtree_target_cloud_.reset(new pcl::KdTreeFLANN<PointType>());
        kdtree_target_cloud_->setInputCloud(target_cloud_);  
        // LOG(INFO) << "source_cloud: " << source_cloud_->points.size();
    }   
   //禁止拷问构造
    CornerPointsCostFunctor(const CornerPointsCostFunctor&) = delete;
    //禁止赋值构造
    CornerPointsCostFunctor& operator= (const CornerPointsCostFunctor&) = delete;
 //这位一个函数模板，ceres中格式固定哈，函数的形参可以按照我们想要的设计，这里直观解释
 //translation描述的是我们需要求解的平移，这里是一个指针，具体类型通常为double 大小为3以此表示我们要求解的x，y，z
 //rotation描述的是我们要求解的旋转，这里是一个指针，具体类型通常为double 大小为4以此表示我们要求解的四元素
  template <typename T>
  bool operator()(const T* const translation, const T* const rotation,
                  T* const residual) const {
    //把平移转化为矩阵形式
    const Eigen::Matrix<T, 3, 1> trans = Eigen::Map<const Eigen::Matrix<T, 3, 1>>(translation);                        
    //把旋转转化为矩阵形式
    const Eigen::Quaternion<T> qua = Eigen::Quaternion<T>(rotation[0], rotation[1], rotation[2], rotation[3]);
    return Evaluate(trans, qua, residual);
  }  
  //这里我们先介绍下思路
  //1 首先我们要遍历当前帧的所有角点Ci
  //2 我们要依据传入，也就是我们要求解的pose，把Ci转到localmap坐标系下Cwi
  //3 由于求解的pose是带先验值的（也就是im预积分的预测值），因此Cwi与在localmap中对应角点距离很近，lio-sam中认为1米以内均为对应,搜索对应5个角点
  //4 计算这5个交点的主成分方向，也就是最大特征值对应的特征向量方向（这里通俗解释就是他妈拟合直线）
  //5 然后计算点到直线的距离，即为残差
  template <typename T>
  bool Evaluate(const Eigen::Matrix<T, 3, 1>& trans, const Eigen::Quaternion<T>& qua,
                T* const residual) const {
    //1 遍历 source_cloud_中所有的角点
    for(size_t i = 0; i < source_cloud_->points.size(); i++) {
      const Eigen::Matrix<T, 3, 1> point(T(source_cloud_->points[i].x),  
                                         T(source_cloud_->points[i].y), 
                                         T(source_cloud_->points[i].z));
      //角点在世界坐标系下的坐标
      Eigen::Matrix<T, 3, 1> corner_point_world =  qua * point + trans;
      //寻找最近的5个角点
      std::vector<int> pointSearchInd;
      std::vector<float> pointSearchSqDis;        
      PointType point_sel;
      const Eigen::Vector3f corner_point_worldf = JetTo(corner_point_world[0], corner_point_world[1], corner_point_world[2]);
      point_sel.x = corner_point_worldf.x();
      point_sel.y =  corner_point_worldf.y();
      point_sel.z =  corner_point_worldf.z();
      // LOG(INFO) << "point_sel: " << point_sel.x << ", " << point_sel.y << ", " << point_sel.z;
      point_sel.intensity = source_cloud_->points[i].intensity;
      kdtree_target_cloud_->nearestKSearch(point_sel, 5, pointSearchInd, pointSearchSqDis); //在附近点云中,找到最近的5个角点
      //计算5个点构成的直线
        double scaling_factor = scaling_factor_;
        //搜索得到相邻的5个点,最远的点距离当前帧的这个角点,不能超过1m
      if (pointSearchSqDis[4] >= 1.0) {
          scaling_factor = 0; //太远的残差丢弃，权重给到0，最后残差就会为0，不优化
          // LOG(INFO) << "error: " << pointSearchSqDis[4];
      }
      //以下为求解特征值和特征向量
      Eigen::Matrix3f matA1 = Eigen::Matrix3f::Zero();
      Eigen::Vector3f matD1 = Eigen::Vector3f::Zero();
      Eigen::Matrix3f matV1 = Eigen::Matrix3f::Zero();
      float cx = 0, cy = 0, cz = 0;
      for (int j = 0; j < 5; j++) {
          cx += target_cloud_->points[pointSearchInd[j]].x;
          cy += target_cloud_->points[pointSearchInd[j]].y;
          cz += target_cloud_->points[pointSearchInd[j]].z;
          // LOG(INFO) << "neraby points: " <<  target_cloud_->points[pointSearchInd[j]].x << ", " <<  target_cloud_->points[pointSearchInd[j]].y << ", " << target_cloud_->points[pointSearchInd[j]].z;
      }
      cx /= 5; cy /= 5; cz /= 5;  //得到5个点的中心点
      float a11 = 0, a12 = 0, a13 = 0, a22 = 0, a23 = 0, a33 = 0;
      for (int j = 0; j < 5; j++) {
          float ax = target_cloud_->points[pointSearchInd[j]].x - cx;
          float ay = target_cloud_->points[pointSearchInd[j]].y - cy;
          float az = target_cloud_->points[pointSearchInd[j]].z - cz;
          a11 += ax * ax; a12 += ax * ay; a13 += ax * az;
          a22 += ay * ay; a23 += ay * az; a33 += az * az;
      }
      a11 /= 5; a12 /= 5; a13 /= 5;
      a22 /= 5; a23 /= 5; a33 /= 5;
      matA1(0, 0) = a11; matA1(0, 1) = a12; matA1(0, 2) = a13;
      matA1(1, 0) = a12; matA1(1, 1) = a22; matA1(1, 2) = a23;
      matA1(2, 0) = a13; matA1(2, 1) = a23; matA1(2, 2) = a33;
      //这里用loam中的eigen求解，原文用的是我下面注释的opencv求解
      //说下差异eigen特征值为从小到大排列，对应特征向量按列存放
 		//opencv特征值为从大到小排列，对应特征向量按行存放
      Eigen::SelfAdjointEigenSolver<Eigen::MatrixXf> solver(matA1);//特征值分解
      //特征值
      matD1 = solver.eigenvalues();  //特征值,也就是主成分的值
      matV1 = solver.eigenvectors(); //特征向量,也就是主成分的向量

      // LOG(INFO) << "matD1: " << matD1(0) << ", " << matD1(1) << ", " <<  matD1(2);
      // LOG(INFO) << "mat0: " << matV1(0, 0) << ", " << matV1(0, 1) << ", " << matV1(0, 2);
      // LOG(INFO) << "mat1: " << matV1(1, 0) << ", " << matV1(1, 1) << ", " << matV1(1, 2);
      // LOG(INFO) << "mat2: " << matV1(2, 0) << ", " << matV1(2, 1) << ", " << matV1(2, 2);

     // {
          //cv::Mat matA1(3, 3, CV_32F, cv::Scalar::all(0));
          //cv::Mat matD1(1, 3, CV_32F, cv::Scalar::all(0));
          //cv::Mat matV1(3, 3, CV_32F, cv::Scalar::all(0));

          //matA1.at<float>(0, 0) = a11; matA1.at<float>(0, 1) = a12; matA1.at<float>(0, 2) = a13;
          //matA1.at<float>(1, 0) = a12; matA1.at<float>(1, 1) = a22; matA1.at<float>(1, 2) = a23;
          //matA1.at<float>(2, 0) = a13; matA1.at<float>(2, 1) = a23; matA1.at<float>(2, 2) = a33;
          //cv::eigen(matA1, matD1, matV1);
          // LOG(INFO) << "111matD: " << matD1.at<float>(0, 0) << ", " << matD1.at<float>(0, 1) << ", " <<  matD1.at<float>(0, 2);
          // LOG(INFO) << "111mat0: " << matV1.at<float>(0, 0) << ", " << matV1.at<float>(0, 1) << ", " <<matV1.at<float>(0, 2);
          // LOG(INFO) << "111mat0: " << matV1.at<float>(1, 0) << ", " << matV1.at<float>(1, 1) << ", " <<matV1.at<float>(1, 2);
          // LOG(INFO) << "111mat0: " << matV1.at<float>(2, 0) << ", " << matV1.at<float>(2, 1) << ", " <<matV1.at<float>(2, 2);
      //}
      //第一主成分要特别的大,是第二的三倍以上
      //对于这个的理解，就是5个点要在一个直线上，其他的特征值就会很小，不在一个直线上说明不表示对应的是一个棱，看我上面画的丑陋的图
      if (matD1(2) <= 3 * matD1(1)) {
          scaling_factor = 0;
          // LOG(INFO) << "error";
      }
      T& x0 = corner_point_world[0];
      T& y0 = corner_point_world[1];
      T& z0 = corner_point_world[2];
      //x1和与y1为线上的两个线上的两个点
      double x1 = cx + 0.1 * matV1(0, 2); //踩点,也就是将这5个附近角点的中心点,向主成分方向,向←向→进行了小幅度移动,又得到了两个点
      double y1 = cy + 0.1 * matV1(1, 2);
      double z1 = cz + 0.1 * matV1(2, 2);
      // LOG(INFO) << "x1: " << x1 << ", y1: " << y1  << ", z1: " << z1;
      double x2 = cx - 0.1 * matV1(0, 2);
      double y2 = cy - 0.1 * matV1(1, 2);
      double z2 = cz - 0.1 * matV1(2, 2);
      // LOG(INFO) << "x2: " << x2 << ", y2: " << y2  << ", z2: " << z2;    
      //由这两个点,和当前帧的那个角点,构成了了一个△;其中那两个点是底边,而当前帧的那个角点为顶点,其误差项就是顶点开向底边的高h;
      T a012 =
          ceres::sqrt(((x0 - x1) * (y0 - y2) - (x0 - x2) * (y0 - y1)) * ((x0 - x1) * (y0 - y2) - (x0 - x2) * (y0 - y1)) +
                ((x0 - x1) * (z0 - z2) - (x0 - x2) * (z0 - z1)) * ((x0 - x1) * (z0 - z2) - (x0 - x2) * (z0 - z1)) +
                ((y0 - y1) * (z0 - z2) - (y0 - y2) * (z0 - z1)) * ((y0 - y1) * (z0 - z2) - (y0 - y2) * (z0 - z1)));

      double l12 = ceres::sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) + (z1 - z2) * (z1 - z2));
      T ld2 = a012 / l12;  // x0 到(x1,y1),(x2,y2)构成直线的距离
      // LOG(INFO) << "ld2: " << ld2;
     //文中认为残差大的适当调小权重，这里被我干掉了
      // T s = 1. - 0.9 * ceres::abs(ld2);  //动态权重，残差越大权重越小
      // const double resi = scaling_factor  * ld2;
      //  LOG(INFO) << "s: " << s << ", scaling_factor: " << scaling_factor ;
      // LOG(INFO) << "resi: " << resi;
      residual[i] = scaling_factor  /* s*/ * ld2;//最终残差
      if(a012 == T(0.)) {
        residual[i] = T(0.);
      }
    }
    return true;
  }
private:
    const double scaling_factor_;
    pcl::PointCloud<PointType>::ConstPtr source_cloud_; 
    pcl::PointCloud<PointType>::ConstPtr target_cloud_;
    pcl::KdTreeFLANN<PointType>::Ptr kdtree_target_cloud_;
};

实现扫描匹配

namespace {
class CeresPose {
 public:
  CeresPose(
       Eigen::Affine3d rigid,
      std::unique_ptr<ceres::LocalParameterization> translation_parametrization,
      std::unique_ptr<ceres::LocalParameterization> rotation_parametrization,
      ceres::Problem* problem);
  CeresPose(const CeresPose&) = delete;
  CeresPose& operator=(const CeresPose&) = delete;
  double* translation() { return translation_.data(); }
  double* rotation() { return rotation_.data(); }
 public:
  std::array<double, 3> translation_;
  // Rotation quaternion as (w, x, y, z).
  std::array<double, 4> rotation_;
};
CeresPose::CeresPose(
     Eigen::Affine3d rigid,
    std::unique_ptr<ceres::LocalParameterization> translation_parametrization,
    std::unique_ptr<ceres::LocalParameterization> rotation_parametrization,
    ceres::Problem* problem)
    : translation_({{rigid.translation().x(), rigid.translation().y(),
                     rigid.translation().z()}})/*,
      rotation_({{rigid.rotation().w(), rigid.rotation().x(),
                  rigid.rotation().y(), rigid.rotation().z()}})*/ {
  Eigen::Quaterniond   a;
  a  = rigid.rotation().matrix(); 
  rotation_ =   {{a.w(), a.x(), a.y(), a.z()}};           
  problem->AddParameterBlock(translation_.data(), 3,
                             translation_parametrization.release());
  problem->AddParameterBlock(rotation_.data(), 4,
                             rotation_parametrization.release());
}
}  // namespace


bool Match( Eigen::Affine3d initial_pose_estimate, 
                     pcl::PointCloud<PointType>::ConstPtr source_corner_cloud, pcl::PointCloud<PointType>::ConstPtr target_corner_cloud, 
                     pcl::PointCloud<PointType>::ConstPtr source_surf_cloud, pcl::PointCloud<PointType>::ConstPtr target_surf_cloud, 
                     Eigen::Affine3d * pose_estimate, ceres::Solver::Summary* const summary  ) const {
  ceres::Problem problem;
  CeresPose ceres_pose(
      initial_pose_estimate, nullptr /* translation_parameterization */,
      //这个必须加上，否则求解为异常
      std::unique_ptr<ceres::LocalParameterization>(
                std::make_unique<ceres::QuaternionParameterization>()),
      &problem);  
if(target_corner_cloud->points.size() > 4) {//目标角点的数量要大于4
    CHECK_GT(options_.corner_weight, 0.);
    // //添加角点loss
    problem.AddResidualBlock(
        new ceres::AutoDiffCostFunction<CornerPointsCostFunctor,
                                        ceres::DYNAMIC, 3, 4>( //ceres::DYNAMIC表示残差的维度动态求解，维度在哪里呢，！所在位置  3 表示ceres_pose.translation()维度x,y,z 3个数 4表示ceres_pose.rotation()四元素 4个数
            new CornerPointsCostFunctor(
                //这里描述的是整体权重，每一个点的权重要除以个数
                options_.corner_weight /
                    std::sqrt(static_cast<double>(source_corner_cloud->points.size())),
                source_corner_cloud, target_corner_cloud),
                source_corner_cloud->points.size()), //！残差维度
                nullptr, ceres_pose.translation(), ceres_pose.rotation());
  } 
  ceres::Solver::Options ceres_solver_options;
  ceres_solver_options.use_nonmonotonic_steps = false;
  ceres_solver_options.max_num_iterations = 20;
  ceres_solver_options.num_threads = 2;          
  ceres_solver_options.linear_solver_type = ceres::DENSE_QR;
  ceres::Solve(ceres_solver_options, &problem, summary);
  Eigen::Translation3d trans(ceres_pose.translation()[0],
                             ceres_pose.translation()[1], 
                             ceres_pose.translation()[2]);
	Eigen::Quaterniond quater(ceres_pose.rotation()[0],ceres_pose.rotation()[1],
	                          ceres_pose.rotation()[2],ceres_pose.rotation()[3]);
	*pose_estimate = trans*quater.toRotationMatrix();
}

未完待续。。。
用ceres实现lio-sam平面点匹配

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/899000.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

学习笔记230802---vue项目手写css样式二次悬浮状态问题

学习笔记230802---vue项目手写css样式二次悬浮状态问题

问题描述 今天在开发页面时&#xff0c;遇到一个很棘手的问题&#xff0c;需求页面做一个卡片效果&#xff0c;鼠标悬浮在卡片上&#xff0c;出现一个选项卡&#xff0c;鼠标悬浮每一项&#xff0c;文字和图标都要变成选中状态的颜色。选项卡的每一项都是通过数据循环渲染来的…
阅读更多...
Selenium自动化测试面试必备：高频面试题及答案整理

Selenium自动化测试面试必备：高频面试题及答案整理

自动化测试已经成为现代软件测试中不可或缺的一部分。在自动化测试中&#xff0c;Selenium是最受欢迎的工具之一&#xff0c;因为它可以模拟用户与Web应用程序的交互。因此&#xff0c;对于许多测试工程师来说&#xff0c;熟练掌握Selenium框架是非常重要的。如果你正在寻找一份…
阅读更多...
CW12B-3A-RCWW12B-6A-RCW12B-10A-RCWW12B-20A-RCWW12B-30A-RCWW12B-40A-R导轨式滤波器

CW12B-3A-RCWW12B-6A-RCW12B-10A-RCWW12B-20A-RCWW12B-30A-RCWW12B-40A-R导轨式滤波器

CW4L2-3A-R1 CW4L2-6A-R1 CW4L2-10A-R1 CW4L2-20A-R1 CW4L2-30A-R1导轨式滤波器 CW12B-3A-R CWW12B-6A-R CW12B-10A-R CWW12B-20A-R CWW12B-30A-R CWW12B-40A-R导轨式滤波器 CW12C-3A-R CWW12C-6A-R CWW12C-10A-R CW12C-20A-R CW12C-30A-R导轨式滤波器 CW4L2-3A-R…
阅读更多...
Python学习之操作XML文件详解

Python学习之操作XML文件详解

概要 我们经常需要解析用不同语言编写的数据&#xff0c;Python 提供了许多第三方库来解析或拆分用其他语言编写的数据&#xff0c;今天我们来学习下 Python XML 解析器的相关功能。 什么是 XML&#xff1f; XML 是可扩展标记语言&#xff0c;它在外观上类似于 HTML&#xff…
阅读更多...
all in one之安装zerotier（第四章）

all in one之安装zerotier（第四章）

好像zerotier国内ipv4不能使用 pve安装zerotier 内网穿透软件总结参考 安装参考教程 安装命令&#xff1a; curl -s https://install.zerotier.com | sudo bash官网 如果有以下问题&#xff0c;进行解决&#xff0c;如果没有则跳过。 问题&#xff1a;-bash: sudo: comman…
阅读更多...
每天一道leetcode：127. 单词接龙（图论困难建图广度优先遍历）

每天一道leetcode：127. 单词接龙（图论困难建图广度优先遍历）

今日份题目&#xff1a; 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk&#xff1a; 每一对相邻的单词只差一个字母。 对于 1 < i < k 时&#xff0c;每个 si 都在 wordList 中…
阅读更多...
2023全网Mysql 合集（25w字）附课程 从安装到高级，实战

2023全网Mysql 合集（25w字）附课程 从安装到高级，实战

mysql学习 1.安装mysql 安装教程 2.mysql的详细学习教程 mysql的详细教程 3.mysql 的高级优化 MySQL高级篇&#xff08;SQL优化、索引优化、锁机制、主从复制&#xff09; 4.MySQL 面试 MySQL数据库面试题总结 二.mysql实战 一、创建数据表并插入数据 1、学生表 Stud…
阅读更多...
【python办公自动化】PysimpleGUI中的popup弹窗中的按钮设置居中

【python办公自动化】PysimpleGUI中的popup弹窗中的按钮设置居中

PysimpleGUI中的popup弹窗中的按钮设置居中 背景问题解决背景 默认的popup弹窗中的OK按钮是在最下面偏左侧一些，有时需要将按钮放置居中 问题解决 首先找到pysimplegui源代码文件中popup的部分 然后定位到19388行，源文件内容如下 关于popup弹窗OK按钮的设置，将pad属性…
阅读更多...
C语言好题解析（三）

C语言好题解析（三）

目录 选择题一选择题二选择题三选择题四编程题一编程题二 选择题一 以下程序段的输出结果是&#xff08;&#xff09;#include<stdio.h> int main() { char s[] "\\123456\123456\t"; printf("%d\n", strlen(s)); return 0; }A: 12 B: 13 …
阅读更多...
《算法竞赛·快冲300题》每日一题：“糖果配对”

《算法竞赛·快冲300题》每日一题：“糖果配对”

《算法竞赛快冲300题》将于2024年出版&#xff0c;是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码&#xff0c;以中低档题为主&#xff0c;适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 糖…
阅读更多...
使用自己的领域数据扩充baichuan模型词表（其他模型也一样）

使用自己的领域数据扩充baichuan模型词表（其他模型也一样）

文章目录 前言环境项目结构一、使用步骤二、训练词表三、合并词表四、效果前言 总的来说，扩充词表可以加快解码速度，对于对中文支持不太友好的模型（如llama），扩充词表还能提升模型在中文的表现。 环境 jsonlines==3.1.0 sentencepiece==0.1.99 transformers==4.28.1项目…
阅读更多...
【Golang系统开发】搜索引擎(3) 压缩倒排索引表

【Golang系统开发】搜索引擎(3) 压缩倒排索引表

写在前面 假设我们的数据集中有 800000 篇文章&#xff0c;每篇文章有 200 词条&#xff0c;每个词条有6个字符&#xff0c;倒排记录数目是 1 亿。那么如果我们倒排索引表中单单记录文档id&#xff0c;不记录文档内的频率和偏移信息。 那么 文档id 的长度就必须是 l o g 2 8…
阅读更多...
04.Show, Attend and Tell

04.Show, Attend and Tell

目录 前言泛读摘要IntroductionRelated Work小结 精读编码器&#xff1a;特征卷积解码器&#xff1a;LSTM网络随机硬注意力和确定软注意力机制硬注意力软注意力双重随机注意力 训练实验数据集评估过程定量分析定性分析 结论 代码&#xff08;略&#xff09; 前言 本课程来自深…
阅读更多...
前端单点登录SSO面试回答

前端单点登录SSO面试回答

JWT鉴权机制 1.JWT用于登录身份验证 2.用户登录成功后&#xff0c;后端通过JWT机制生成一个token&#xff0c;返回给客户端 3.客户端后续的每次请求都需要携带token&#xff0c;放在header的authorization中 4.后端从authorization中拿到token后&#xff0c;通过secretKey进…
阅读更多...
密码学学习笔记(二十)：DSA签名与X.509证书

密码学学习笔记(二十)：DSA签名与X.509证书

数字签名 下图是一个制作以及使用数字签名过程的通用模型。 假设Bob发送一条消息给Alice&#xff0c;尽管消息并不重要&#xff0c;也不需要保密&#xff0c;但他想让Alice知道消息确实是他本人发的。出于这个目的&#xff0c;Bob利用一个安全的散列函数&#xff0c;比如SHA-…
阅读更多...
elaticsearch(1)

elaticsearch(1)

1.简介 Elasticsearch是一个开源的高扩展的分布式全文检索引擎&#xff0c;它可以近乎实时的存储、检索数据&#xff1b;本身扩展性很好&#xff0c;可以扩展到上百台服务器&#xff0c;处理PB级别的数据。 Elasticsearch也使用Java开发并使用Lucene作为其核心来实现所有索引…
阅读更多...
【C++ 记忆站】引用

【C++ 记忆站】引用

文章目录 一、引用概念二、引用特性1、引用在定义时必须初始化2、一个变量可以有多个引用3、引用一旦引用一个实体&#xff0c;再不能引用其他实体 三、常引用四、使用场景1、做参数1、输出型参数2、大对象传参 2、做返回值1、传值返回2、传引用返回 五、传值、传引用效率比较六…
阅读更多...
电脑提示msvcp140.dll丢失的解决方法,dll组件怎么处理

电脑提示msvcp140.dll丢失的解决方法,dll组件怎么处理

Windows系统有时在打开游戏或者软件时&#xff0c; 系统会弹窗提示缺少“msvcp140.dll.dll”文件 或者类似错误提示怎么办&#xff1f; 错误背景&#xff1a; msvcp140.dll是Microsoft Visual C Redistributable Package中的一个动态链接库文件&#xff0c;它在运行软件时提…
阅读更多...
Scratch 之 算法教程 -- 递归

Scratch 之 算法教程 -- 递归

递归是指物体表现出相似的重复性。它在生活中很常见&#xff0c;如俄罗斯套娃、汉诺塔游戏、分形图案&#xff08;科赫雪花、谢尔宾斯三角形等&#xff09;、两个面对面的镜子、斐波那契数列&#xff0c;二叉树等 在计算机科学中&#xff0c;递归是指函数定义中重复调用自己的行…
阅读更多...
【高频面试题】 消息中间件

【高频面试题】 消息中间件

文章目录 1、RabbitMQ1.1 RabbitMQ-如何保证消息不丢失1.2 RabbitMQ消息的重复消费问题如何解决的1.3 RabbitMQ中死信交换机 ? (RabbitMQ延迟队列有了解过嘛)1.4 RabbitMQ如果有100万消息堆积在MQ , 如何解决(消息堆积怎么解决)1.5 RabbitMQ的高可用机制有了解过嘛 2、Kafka2.…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023