《算法竞赛·快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。
文章目录
- 题目描述
- 题解
- C++代码
- Java代码
- Python代码
“ 糖果配对” ,链接: http://oj.ecustacm.cn/problem.php?id=1735
题目描述
【题目描述】 现在有N个小朋友,有M个不同的糖果。每个小朋友有自己最喜欢的糖果和第二喜欢的糖果。
给定一些糖果,小朋友们会排队来领糖果,对于每个小朋友而言,如果其最喜欢的糖果还在,将会选择最喜欢的糖果,否则选择第二喜欢的糖果。
如果二者都不在,那么这个小朋友将会哇哇大哭。
你可以任意排列对小朋友排队的顺序,但是要保证哭的小朋友数量最小。
请求出最小的哭泣小朋友的数量。
【输入格式】 输入格式
输入第一行包含N和M。(N,M≤100000)
接下来有N行,每i行包含两个数字fi和si表示第i个小朋友最喜欢和第二喜欢的糖果编号。
【输出格式】 输出一个数字表示答案。
【输入样例】
8 10
2 1
3 4
2 3
6 5
7 8
6 7
7 5
5 8
【输出样例】
1
题解
每个孩子有最喜欢的糖果和次喜欢的糖果,从二者中选择一个,相当于一个孩子连接了两个糖果。把孩子和糖果建模为一个图,孩子是图上的边,糖果是图上的点。要求每条边和每个点进行配对,问最多有多少个点和边能够匹配?
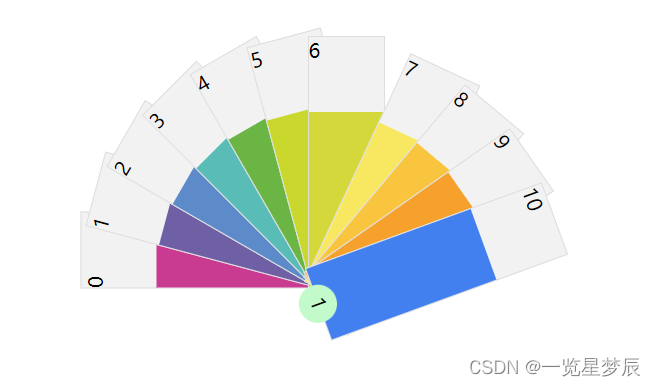
把样例画成下面的图,图中的边是孩子,点是孩子喜欢的糖果。例如边{1-2}是第1个孩子喜欢的糖果1、2。根据样例的数据画出2个连通子图,一个子图是{1,2,3,4},它是一棵树;一个子图是{5,6,7,8},它是一个有环图。
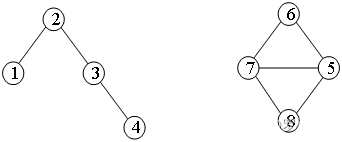
容易分析得出:如果连通子图是一棵树,则匹配的数量就等于边数,或者等于点的数量减一;如果连通子图是一个有环图,匹配的数量就等于点数。例如上图中,左边子图是有3条边的树,能满足3个小朋友;右边子图是有4个点的有环图,能满足4个小朋友。
本题经过转换后是这样一个图的连通性问题:(1)构造图;(2)查询其中有多少连通子图;(3)对每个子图,区分它是树还是有环图,分别统计边和点的数量。
图的连通性,编码可以用BFS、DFS、并查集。下面用编码比较简单的并查集求解。
首先读取点和边,用并查集处理,属于同一个子图的点,它们的集都相同,同时用ring标注这个集是否是有环图。
如何用并查集处理有环图?读2个点u、v构成的边u-v时,如果发现u、v已经在以前读取和处理过,且属于一个集,说明边u-v把原来的子图变成了一个有环图。
读取和处理完所有的点和边后,上面图示的的两个子图变成了下面的两个并查集。并查集2中包含点{1, 2, 3, 4},并查集6中包含点{5, 6, 7, 8}。
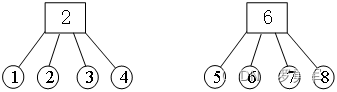
请注意两个关键:
(1)并查集必须用路径压缩,这样才能使得一个集中的每个点所属的集相同,例如{1, 2, 3, 4}都属于并查集2。
(2)需要标记每个并查集是树还是有环图。下面的代码用参数ring来标记一个点是否在有环图上。只要这个并查集中有一个点的ring标记为true,这个并查集就是一个有环图。
最后就是搜索有多少并查集,并统计每个并查集内部有多少个糖果匹配。只需用O(nlogn)的计算量即可完成这2个任务:
(1)对所有并查集按集的大小排序,例如{1, 2, 3, 4}、{5, 6, 7, 8}这个两个并查集的点对应的集是{2, 2, 2, 2}、{6, 6, 6, 6},按集的大小排序后,同一个集的点都排在一起。排序的计算量为O(nlogn)。
(2)从小到大遍历所有的集,如果集的大小一样,它们就属于一个集。统计这个集内部的糖果匹配数量。计算量为O(n)。
【重点】 图的连通性 。
C++代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
struct child {int s; bool ring;} c[N]; //s: 并查集; ring:这个点是否在一个有环图上
bool cmp(struct child a, struct child b){ return a.s < b.s;} //按s排序
int find_set(int x){ //并查集:查询
if(c[x].s!=x) c[x].s=find_set(c[x].s); //路径压缩
return c[x].s;
}
int main(){
int n,m; cin>>n>>m;
for(int i=1;i<=m;i++) c[i].s = i,c[i], c[i].ring = false; //并查集初始化
for(int i=1;i<=n;i++) {
int u,v; cin>>u>>v; //读取一条边上的两个点
u = find_set(u); //查询它们的集
v = find_set(v);
if(u==v){ //已经是同一个集,说明这个集是一个有环图
c[u].ring = true; //标注这个集是一个有环图
continue; //已经在一个集中了,不用合并
}
c[v].s = c[u].s; //u、v还不在一个集中,进行并查集合并
}
for(int i=1;i<=m;i++)
find_set(i); //利用查询进行路径压缩,使同一个集的点的所属的集相同
sort(c+1,c+m+1,cmp); //对集排序,让同一个集的点排在一起
int tot = 0; //统计能满足多少小朋友
for(int i=2;i<=m;i++) { //遍历有多少个集
bool Ring = false; //这个集是否为有环图,初始化为非环图
int point = 1; //统计这个集表示的连通子图内有多少个点
while(c[i].s == c[i-1].s) { //如果两点的集s相同,说明它们属于同一个子图
if(c[i-1].ring || c[i].ring ) Ring = true; //这个集是一个有环图
point++; //统计这个集合的点的数量
i++; //遍历这个集
}
if(Ring==false) point--; //不是有环图,是一棵树
tot += point;
}
cout<<n-tot; //不能满足的小朋友人数
return 0;
}
Java代码
import java.util.*;
public class Main {
static class Child {
int s;
boolean ring;
public Child(int s, boolean ring) {
this.s = s;
this.ring = ring;
}
}
static Child[] c;
static int n, m;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
int N = 100010;
c = new Child[N + 1];
for (int i = 1; i <= N; i++) c[i] = new Child(i, false);
for (int i = 1; i <= n; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
u = findSet(u);
v = findSet(v);
if (u == v) {
c[u].ring = true;
continue;
}
c[v].s = c[u].s;
}
for (int i = 1; i <= m; i++) findSet(i);
Arrays.sort(c, 1, m + 1, new Comparator<Child>() {
public int compare(Child a, Child b) { return a.s - b.s; }
});
int tot = 0;
for (int i = 2; i <= m; i++) {
boolean ring = false;
int point = 1;
while (c[i].s == c[i - 1].s) {
if (c[i - 1].ring || c[i].ring) ring = true;
point++;
i++;
}
if (!ring) point--;
tot += point;
}
System.out.println(n - tot);
}
static int findSet(int x) {
if (c[x].s != x) c[x].s = findSet(c[x].s);
return c[x].s;
}
}
Python代码
import sys
sys.setrecursionlimit(1000000)
import functools
N = 100010
class Child:
def __init__(self, s, ring):
self.s = s
self.ring = ring
def cmp(a, b): return a.s - b.s
def find_set(x):
if c[x].s != x: c[x].s = find_set(c[x].s)
return c[x].s
c = []
n, m = map(int, input().split())
for i in range(N): c.append(Child(i, False))
for i in range(1,n+1):
u, v = map(int, input().split())
u = find_set(u)
v = find_set(v)
if u == v:
c[u].ring = True
continue
c[v].s = c[u].s
for i in range(1, m + 1): find_set(i)
c[1:] = sorted(c[1:], key=functools.cmp_to_key(cmp))
tot = 0
i = 2
while i <= m:
Ring = False
point = 1
while c[i].s == c[i - 1].s:
if c[i - 1].ring or c[i].ring: Ring = True
point += 1
i += 1
if not Ring: point -= 1
tot += point
i += 1
print(n - tot)