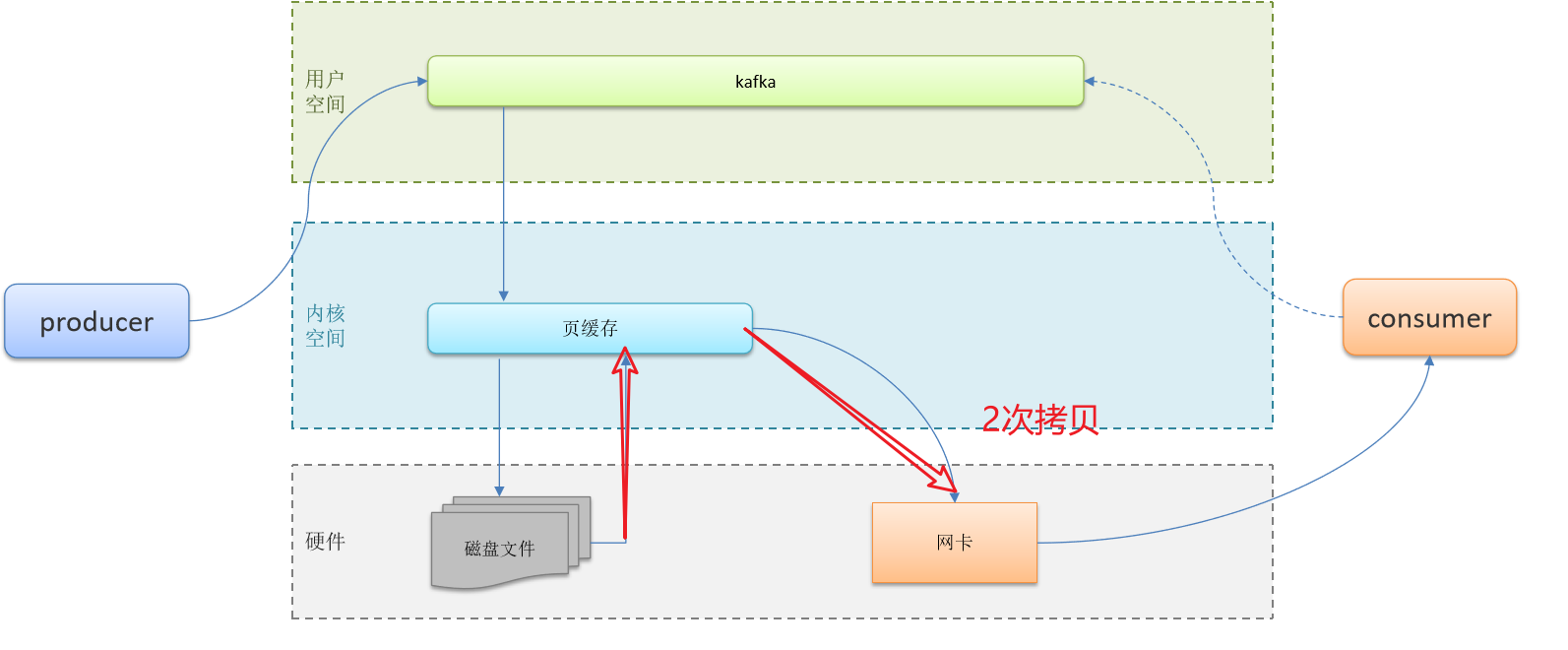
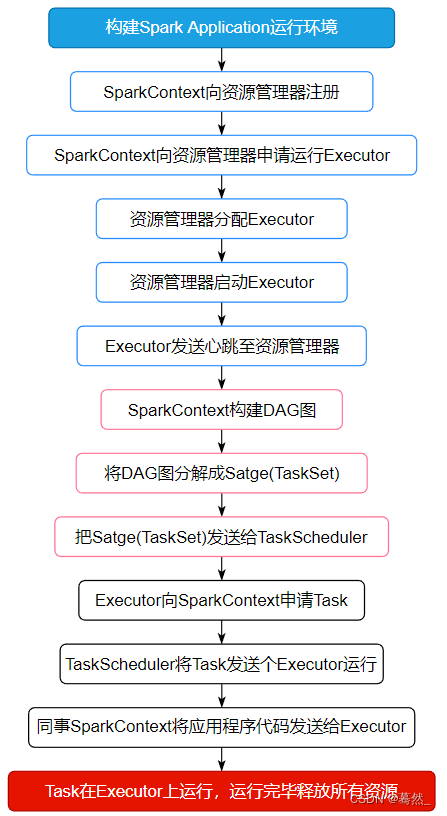
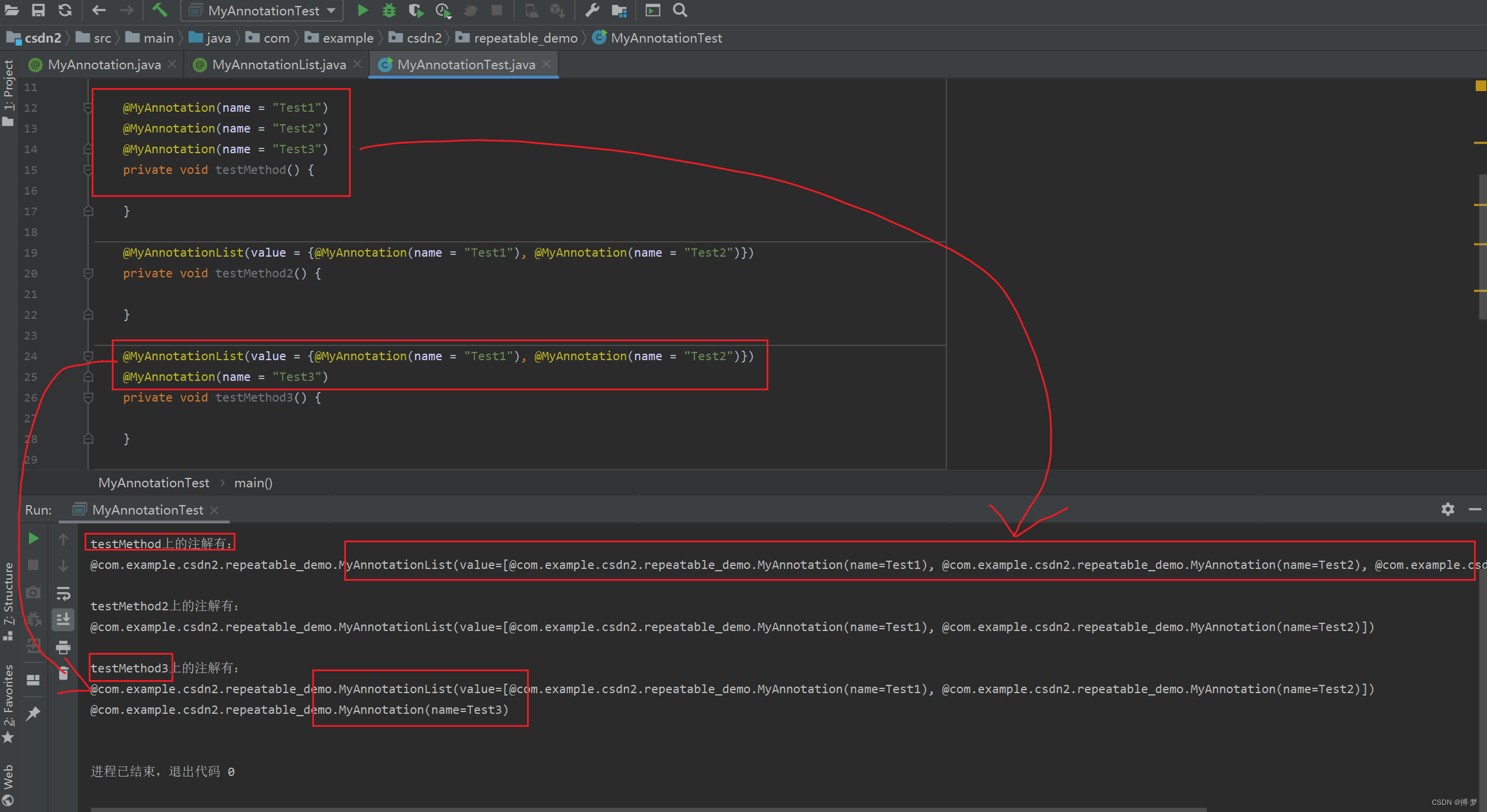
递归是指物体表现出相似的重复性。它在生活中很常见，如俄罗斯套娃、汉诺塔游戏、分形图案（科赫雪花、谢尔宾斯三角形等）、两个面对面的镜子、斐波那契数列，二叉树等

        在计算机科学中，递归是指函数定义中重复调用自己的行为。函数就是scratch中的自定义积木块，也可以称之为过程。其实循环和递归时可以相互转换的，在某些编程语言中（如Haskell）甚至没有循环结构，只能靠递归实现循环效果

最简单的递归案例，秒表滴答作响，同时旋转指针：

 

        和重复执行一样，这段脚本必须借助停止按钮或停止积木才能结束，因为它没有递归终始条件。让我们再来看一个递归的基本案例，求1+2+...+99+100的值。

         这种递归被称为尾递归，也是最好理解的一种递归形式。常用于优化程序执行速度（经测试，scratch使用尾递归不能提升运算速度），因此它不需要回溯。什么是回溯呢？

        上面的求和程序中程序结束后，递归全部结束了,并没有回溯到上一个调用它的函数

        下面我们来看看一个带回溯的递归策略

        递归策略的基本思想是把规模较大的问题转化为规模较小的相似的子问题来解决，特别适用于循环层数不确定的情形，可以看成是非常特殊的迭代形式；从技术角度来说，递归就是自己调用自己的行为，其流程如下：

         递归过程是递归算法中的关键行为，这个关键行为在解决问题中可以不断重复循环，最后递归变量达到结束条件就退出递归函数。如何在问题中找到这个关键行为是较难的，但这也是区分您是否理解递归思想。

---

简单的例题：Tower of Hanoi（汉诺塔）

        将所有n个圆环从0号柱子移到1号柱子。注意：不能将较大的圆环放在较小的圆环之上。（选自并改编自梵塔的终极挑战与梵塔的灭世预言）

         我们不妨从简单的问题开始思考：现在0号柱子上有2个金片，你需要将它们全部移到1号柱子。

简单思考可知：

（1）0---->2

（2）0---->1

（3）2---->1

总共需要移动3次

结合递归算法，可以把移动n个盘子简单分为三个步骤：

（1）把n-1个盘子由0移到2；

（2）把第n个盘子由0移到1；

（3）把n-1个盘子由2移到1；

        由于每次只能移动一个盘子，所以在递归时，我们需要判断：当目前需要移动的盘子数=1时，即可移动并返回前一个递归

（1）中间的一步是把最大的一个盘子由0移到1上去；

（2）中间一步之上可以看成把0上n-1个盘子通过借助辅助塔（1塔）移到了2上，

（3）中间一步之下可以看成把2上n-1个盘子通过借助辅助塔（0塔）移到了1上；

递归代码如下：

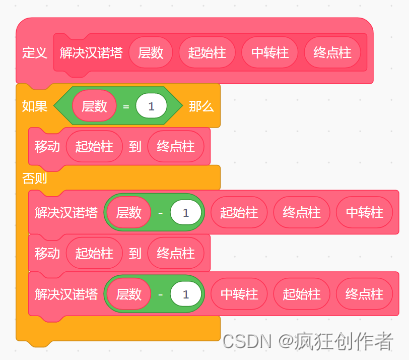
 启动递归代码如下：

 （0作为起始柱，1作为终点柱，2作为中转柱）

---

        因为阶乘的增长速度极快，所以当层数较多时，需要的步数也就非常惊人，这也就说明了为什么64层汉诺塔被移动完毕后世界会毁灭（需要移动2^64-1=1.8446744e+19次）

        递归策略可以很好地描述复杂程序的逻辑，这就是递归算法的意义所在