选择题一

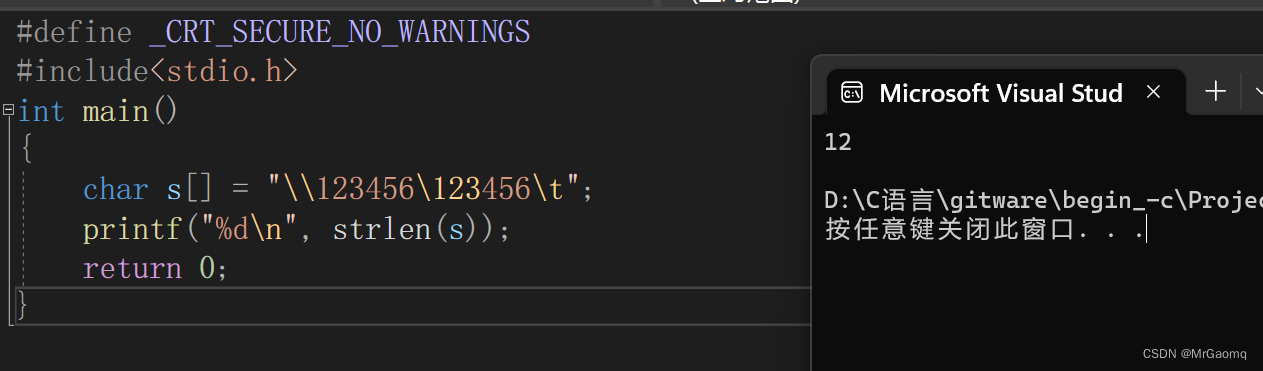
以下程序段的输出结果是（）

#include<stdio.h>
int main()
{
char s[] = "\\123456\123456\t";
printf("%d\n", strlen(s));
return 0;
}

A: 12      B: 13      C: 16     D: 以上都不对

【答案】 A
【分析】这道题涉及到转义字符，\是一种转义字符，而\就是以（第一个\）修饰（第二个\）使（第二个\）不表示转义的意思（这里有点绕）
因此\ \为一个字符，而123456则为6个字符。
对后面的\123456\t来说，\123表示一个字符（\ddd：ddd是表示一个1-3位的八进制数字），而456则表示3个字符，\t表示一个字符。
接下来就是strlen的含义，strlen是计算字符串的长度，直到遇见\0才会停止，因此经过前面的分析，strlen（s）=1+6+1+3+1=12
加粗样式

选择题二

若有以下程序，则运行后的输出结果是（）

#include <stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{
printf("%d\n", NUM);
return 0;
}

A: 4       B: 8       C: 9      D: 6

【答案】 B
【分析】这道题就是替换变量，根据上面的定义我们知道
N=2
M=N+1
NUM=（M+1）*M/2
将等式带入第三表达式即可得出结果。
值得注意的是许多人算出的结果为6，因为他们在算时NUM=（2+1+1）（2+1）/2=6（事实上这道题我也是这样算的）
但是实际上正确的算法为：
NUM=（2+1+1） *2+1/2=8.5
这是因为（M+1）*M的第二个M并没有（）因此在计算时不能擅自添加（）。
最后的8则是因为%d为int的打印方式，所以将小数点后的5省略了
在这里插入图片描述

选择题三

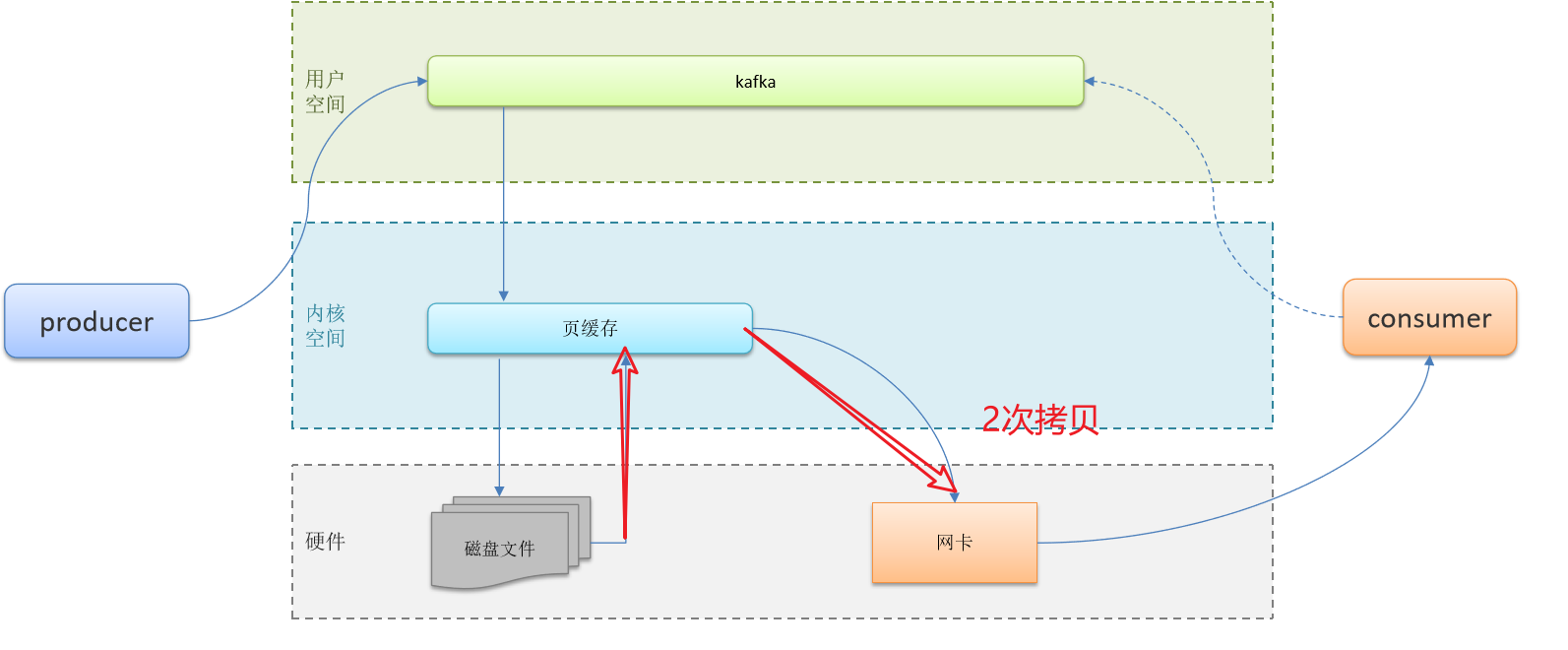
如下函数的 f(1) 的值为（ ）

int f(int n)
{
static int i = 1;
if(n >= 5)
return n;
n = n + i;
i++;
return f(n);
}

A: 5      B: 6       C: 7       D: 8

【答案】C
【分析】这道题是递归类型的题，n>=5为限制条件，但需要注意的是static修饰的i
千万不用以为int i=1，i就一直为1了，static修饰使它可以保留以前变化的值，因此i是一直在增加的
详细的过程如图：
在这里插入图片描述

选择题四

下面3段程序代码的效果一样吗（）

int b;
(1)const int *a = &b;
(2)int const *a = &b;
(3)int *const a = &b;

A: (2)=(3)  B: (1)=(2)  C: 都不一样  D: 都一样

【答案】 B
【分析】我们需要了解const的含义，只要了解了含义就可以做这道题
const是修饰他后面的变量使它的地址或者数值无法改变。
比如：
（1）中const修饰的是a，就说明a无法改变，因为a是表示的地址，所以a所表示的地址无法改变，但是a的值是可以改变的。
（2）中const修饰的仍是*a（和int无关）
（3）const修饰的是a，也就说明a所代表的数值无法改变，但a的地址是可以改变。

编程题一

验证尼科彻斯定理

任何一个整数 m 的立方都可以写成 m 个连续奇数之和
例如
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19
输入一个正整数 m（m≤100） 
将 m 的立方写成 m 个连续奇数之和的形式输出。
注意：本题含有多组输入数据。
输入描述：输入一个int整数
输出描述：输出分解后的string
示例：
输入：6
输出：31+33+35+37+39+41

【题目分析】
我们需要用n将m的立方表示出来，然后由连续奇数之和可以设第一个奇数a1=x，然后由等差数列的求和公式可以算出Sm=m*x+（m-1）2，
即可得出关系式m^3=mx+2 * （m-1） * m
即x=m * m- m+1
因为x为第一项，为了求出x的具体值我们需要用到for循环
【代码】

int main()
{
	int m = 0;
		scanf("%d", &m);
		int n = m * m * m;
		int x = m * m - m + 1;
		for (int i = 1; i <= m; i++)
		{
			if (i == m)
				printf("%d", x);
			else
			{
				printf("%d+", x);
				x += 2;
			}

		}
	return 0;
}

编程题二

等差数列 2，5，8，11，14， … 。（从 2 开始的 3 为公差的等差数列），求等差数列前 n 项和

注意：本题有多组输入
输入描述：输入一个正整数 n 。
输出描述：输出一个相加后的整数
示例：
输入：2 输入：275
输出：7 输出：113575
说明：2+5=7 说明：2+5+...+821+824=113575

【题目分析】
这道题和上一题的解法类似，但是是求的Sn
因此需要设一个sum（即Sn），还有x通过式子sum+=x，x+=3再加上循环即可解决问题
【代码】

#include<stdio.h>
int main()
{
	int n, x = 2, sum = 0;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		sum += x;
		x += 3;
	}
	printf("%d", sum);
	return 0;
}