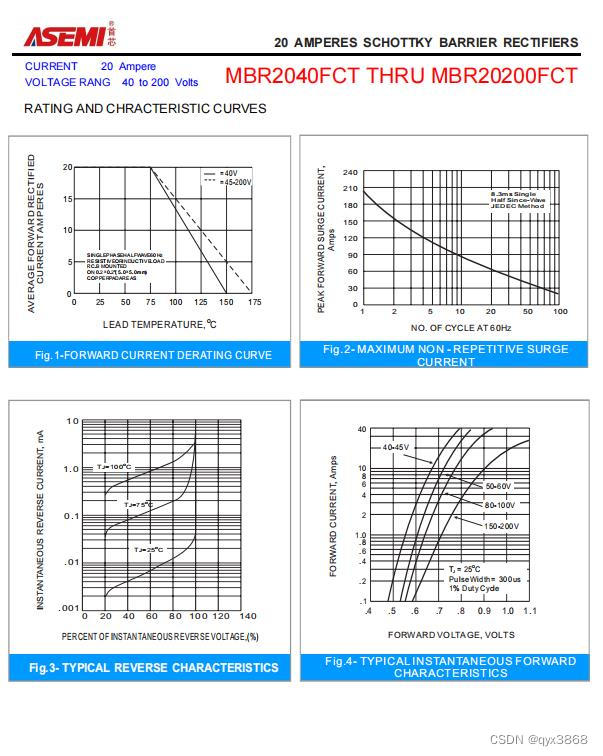
强化学习中Agent与环境的交互过程是由马尔可夫决策过程(Markov Decision Process, MDP)描述的。MDP对环境做了一个假设，称作马尔可夫性质，即下一时刻的状态只由上一时刻的状态和动作决定。
马尔可夫性质决定了值函数(状态值与动作值函数)可以写成递归的形式，即贝尔曼等式：

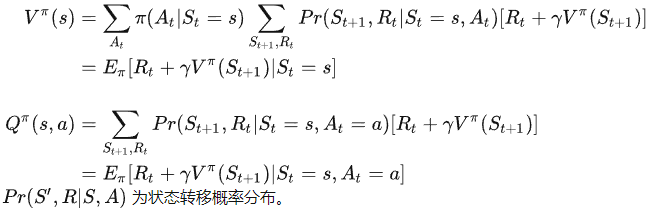
事实上，在很多任务中，或者使用深度神经网络对动作值函数和状态值函数进行参数化拟合时，我们是默认agent执行一个动作后得到的状态的是唯一的。此时，我们可以认为状态转移概率$Pr$是1。
这样的话，我们就可以更方便的理解上面的公式了。

贝尔曼等式清晰地展示了值函数之间的迭代规律，或者说是相邻两个时刻的值函数间的关系: 以状态值函数为例，当前时刻的状态值等于下一时刻的奖励$r_t$与下一时刻的状态值的和的期望。
乍一看，这俩货的递归方法是一样的。除了多了一个动作$a_t$之外，其他地方没有任何区别。
事实上，这两者的区别在于求解最优状态值函数和最优动作值函数时才能变现出来。而人们设计深度强化学习是根据最优值函数的递推关系来设计网络结构的。
例如DQN，他们通过参数化的神经网络$Q(s,a;w)$来表示最优动作值函数$Q^{\ast }(s,a)$。state $s_t$作为DQN的输入，其输出是对每个action $a_t$的价值$Q(s,a_i)$预测，比如left, right和up的价值分别预测2000,1000和3000。这里的$a_i$的下标$i$表示在状态s是agent可以执行的每个动作。

跟进一步的讲，Dueling DQN中，他们把这种思想体现的淋漓尽致。
然我们来梳理一下Dueling DQN的推导过程。主要是优势函数的推导和使用。
首先，强化学习定义了agent在一个轨迹上的累积折扣收益
$G_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+...$

$G_t$ 表示从$t$时刻开始，未来所有奖励的加权求和。在$t$时刻，$G_t$是未知的，它依赖于未来所有状态和动作。

相应的，状态-动作价值函数((Action-value function))可以初步定义为：

$Q_{\pi }((s_t,a_t)=E[G_t|S_t=s_t,A_t=a_t]$

$Q_{\pi }(s_t,a_t)$是回报$G_t$的条件期望，将$t+1$时刻以后的状态和动作全部消掉。$Q_{\pi }(s_t,a_t)$依赖于状态$s_t$、动作$a_t$以及策略$\pi$。

同样，状态值函数(State-value function)可以定义为：

$V_{\pi }(s_t)=E\left[Q_{\pi }(s_t,A)\right]$ （1）

这个公式说明，当前状态$s_t$的状态值函数等于该状态所有动作的状态动作值函数的期望。注意这个公式(1)里的大写的动作$A$。这个很有用啊，兄弟。它是后面推导Dueling DQN的关键呐。纯纯的都是科技与狠活…

为了满足一些把期望都忘记的同学的需求，我举个小小的例子解释一下什么是期望，以离散型为例：
假设张三在玩射击游戏，打气球，共可以射击4次。射中4次的概率是0.1，射中3次的概率是0.4，射中2次的概率是0.3，射中1次的概率是0.1，射中0次的概率是0.2。分别可以得到5元，4元，3元，2元，1元。

那么，这次游戏的期望就是0.15+0.44+0.33+0.22+0.1+1=2.06

这个时候，我们把射中个数的概率当成策略函数$\pi (a|s)$，把得到的钱当做动作值函数。

结合下面这个图，这个公式（1）看这是不是很舒心了？就更明了了。

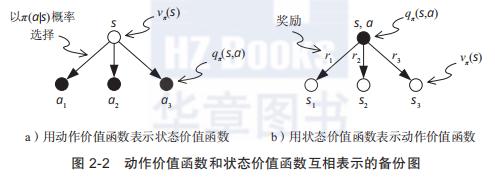
$V_{\pi }(s_t)$ 是$Q_{\pi }(s_t,a_t)$的期望，将$Q_{\pi }(s_t,a_t)$中的动作$a_t$消掉。$V_{\pi }(s_t)$依赖于状态$s_t$ 和策略$\pi (a|s)$。

下面开始了，其实上面说的那些公式都是浮云，深度强化学习的目标是直接拟合最优状态值函数或动作值函数。

所以我们需要对最优动作值函数和最优状态值函数之间的关系进行推导：

直观的，最优动作价值函数(Optimal action-value function):

$Q^{\ast }(s,a)=ma{x}_{\pi }{Q}_{\pi }(s,a)$

我们再回顾一下，DQN的输出是在状态$s$下每个动作的值函数。比方说我们有三个动作，这里的$max()$函数求的就是$Q$值最大的那个动作的动作值函数的值，即$Q^{\ast }(s,a)$

动作价值函数$Q_{\pi }(s_t,a_t)$依赖于策略$\pi$，对$Q_{\pi }(s_t,a_t)$关于$\pi$求最大值，消除掉$\pi$，得到$Q^{\ast }(s,a)$，$Q^{\ast }(s,a)$只依赖于状态$s$和动作$a$，不依赖于策略$\pi$。$Q^{\ast }(s,a)$用于评价在状态$s$下做动作$a$的好坏。

进一步的，我们写一下最优状态值函数
最优状态价值函数(Optimal state_value function):

$V^{\ast }(s_t)=ma{x}_{\pi }{V}_{\pi }(s_t)$ （2）

这个也很好解释，

对$V_{\pi }(s)$关于$\pi$求最大值，消除掉$\pi$，得到$V^{\ast }(s)，V^{\ast }(s)$只依赖于状态$s$， 不依赖于策略$\pi$。$V^{\ast }(s)$用于评价状态$s$的好坏。

回到公式(1)，我直接给复制到这边：
$V_{\pi }(s_t)=E\left[Q_{\pi }(s_t,A)\right]$ （1）
当前状态$s_t$的状态值函数等于该状态所有动作的状态动作值函数的期望。
然后，我们就可以定义优势函数了：
首先说一下优势函数的作用：

优势函数$A(s,a)$用于度量在状态$s$下执行动作a的合理性，它直接给出动作$a$的性能与所有可能的动作的性能的均值的差值。如果该差值(优势)大于0，说明动作$a$优于平均，是个合理的选择；如果差值(优势)小于0，说明动作$a$次于平均，不是好的选择。度量状态$s$下的动作$a$的性能最合适的形式就是动作值函数（即Q函数）$Q^{\pi }(s,a)$；而度量状态s所有可能动作的性能的均值的最合适形式是状态值函数（即V函数） $V^{\pi }(s,a)$ 。

先理解他的作用，然后再看它的公式，就一目了然了：
最优优势函数(Optimal advantage function):

$A^{\ast }(s,a)=Q^{\ast }(s,a)-V^{\ast }(s)$

你看是不是很巧妙，$Q^{\ast }(s,a)$是当前DQN选择的最优动作的Q值，而$V^{\ast }(s)$是对当前所有动作的评价，$Q^{\ast }(s,a)$是对当前DQN选择的动作的评价。如果Q大于零，说明选择对了。如果小于零说明选择错了。

当然，这个$A^{\ast }(s,a)$是理论推导的，在Dueling DQN中是使用神经网络拟合的，即$A^{\ast }(s,a;w)$
然后，我们就有了对$Q^{\ast }(s,a)$的弥补方法：

$Q^{\ast }(s,a;w)=V^{\ast }(s;\alpha )+A^{\ast }(s,a;\beta )$

在这个公式中，$w,\alpha ,\beta$表示拟合这三者的神经网络的参数。
这个公式的想法就是：

针对DQN当前计算的动作的值函数$Q^{\ast }(s,a;w)$，如果DQN计算错了，那么$A^{\ast }(s,a;\beta )$是小于零的，此时就让他减去一点。如果DQN计算对了，那$A^{\ast }(s,a;\beta )$是大于零的，那么就让它更大，从而增加在该状态时选择该动作的优势。

其实，理论推导是很合理的。在表格形强化学习中，这种方法很强，优势很明显。但是，当我们使用神经网络拟合时，其实已经很玄学了。

强化学习1-基础概念(state,action,reward,policy)

强化学习2-动作价值函数&DQN

强化学习笔记3

强化学习中值函数与优势函数的估计方法

深度强化学习-Dueling DQN算法原理与代码