周志华 《机器学习初步》 绪论

Datawhale2022年12月组队学习 ✌

• 周志华老师对西瓜书的使用建议 🐮

  其实之前一直没有把西瓜书读进去，感觉略有些枯燥，翻了几页就感觉不想看， 也许是定位和思路没搞好，感觉老师讲的很好

  “观其大略”→“提纲挈领”→“疏通经络” 这个学习过程放在很多其他地方也适用！

  

• 周志华老师对这门课的定位

  • 老师大致提了一下科学、技术、工程、应用的区别

    自己读的专业是计算机科学与技术，但是好像确实没有仔细思考过哈哈哈

    • 管理“工程”、“科学”、“技术”三者之间有什么区别？ - Maoo的回答 - 知乎 https://www.zhihu.com/question/21687748/answer/43720055

    • 科学：是什么、为什么
    • 技术：怎么做
    • 工程：怎样做得多快好省
    • 应用

  • 周老师这门课主要是 what、why、how （科学与技术）

一.机器学习

• 机器学习经典定义：利用经验改善系统自身的性能 [T.Mitchell 教科书，1997]

  经验在computer里面是以数据形式存在的

• 于是乎，现在可以说它是主要研究 智能数据分析 的理论和方法

  课件里的图不错哈哈， 数据本身不代表价值，需要靠机器学习进行智能分析来挖掘其价值

  

二.典型的机器学习过程

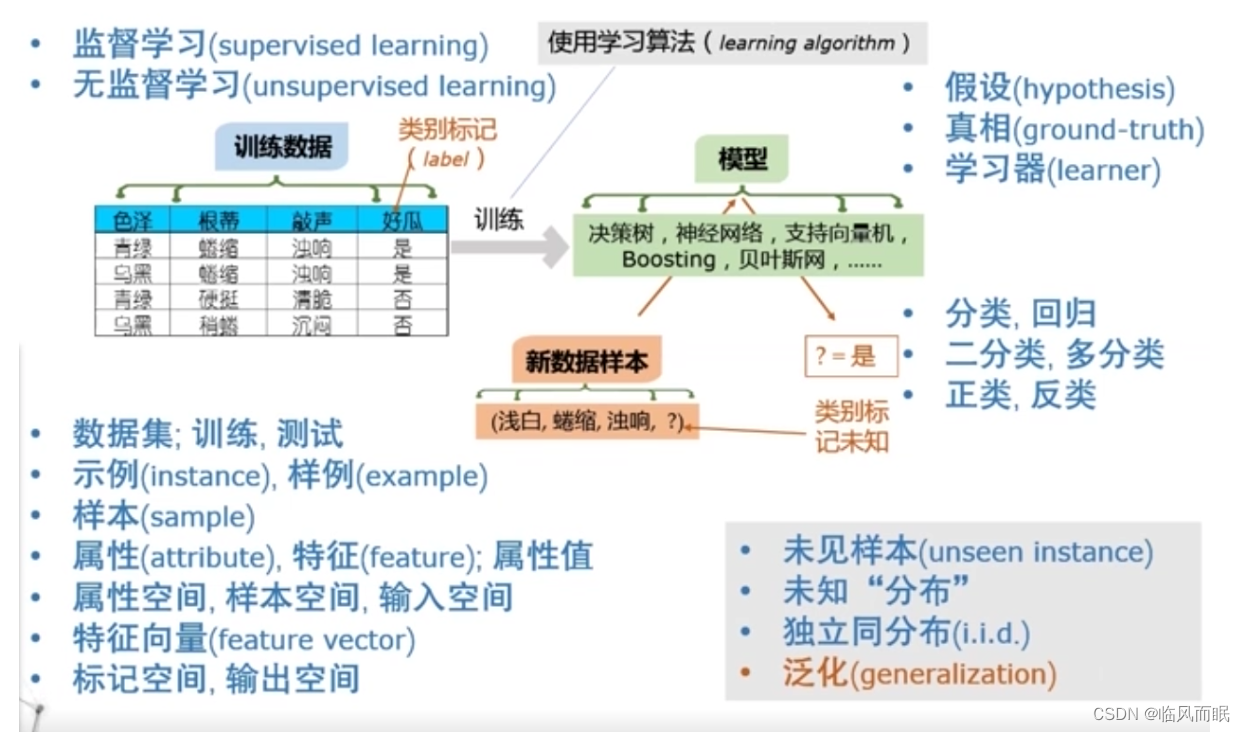
• 老师是以西瓜分类为例来讲的

  

• 首先，收到很多知道结果的数据，历史数据，称为训练数据，假设要做一个细化的分类

  • 如上图，把数据组织成一个表格形式
    • 表格的每一行对应了一个对象或者一个事件
    • 每一列对应的刻画对象或者事件的一个属性，一个特征
    • 把关于结果的东西叫做 类别标记标签，label 标记
  • 比如第一行就是西瓜，颜色是青绿色的，根蒂是蜷缩的，敲起来声音很浑浊，它切开看过，我们知道它是好瓜
  • 比如第三个西瓜，颜色青绿，根蒂硬挺，敲声清脆。切开看，我们知道它不不是好瓜

• 我们经过一个训练过程就得到一个模型，这个模型在这里就是分类模型。

  • 这个模型之后有什么用处？
    • 以后来一个新的数据，把这个数据的描述作为输入提供给这个模型，模型就会产生一个输出
    • 比如上图来了一个一个西瓜摊上还没有切开的西瓜，它颜色是浅白色，根蒂是蜷缩的，声音很浑浊。我们不知道这个瓜好不好，就把它输入到模型里面
  • 所谓的模型是抽象的说法，可理解为从数据中产生出来的一个东西，可以是一个神经网络，甚至是一条规则

• 这个里面从数据到模型，最关键的一步是训练

• 计算机科学是关于算法的学问，如果从这个含义来，机器学习是关于学习算法（learning algorithm）的设计、分析和应用的学问。所以我们研究的核心是学习算法。

  • 学习算法决定了获得什么样的模型，模型的性质很多时候来自于算法。
  • 算法是用到数据上，所以不一定每次都得到同样一个模型。
  • 所以这几方面联系起来之后，我们才能够知道我们整个机器学习的过程最后得到什么。

• 学习过程中要去体会

  • 一个算法针对什么样的数据是有效的
  • 这样的数据需要满足什么样的特点
  • 它产生的模型又是在什么情况下会有效
  • 这样的模型本身具有什么样的特点

三.计算学习理论

PAC模型

• 机器学习有很坚实的理论基础做指导,最重要的一点是Leslie Valiant教授建立的计算学习理论（Computational learning theory）

  

• 其中最重要的一个理论模型是 PAC(Probably Approximately Correct，概率近似正确) 模型

  • PAC模型的基础表达式: $P(|f(\mathbf{x})-y|\le ϵ)\ge 1-\delta$

• 如何理解？

  • 我们要去建立一个模型，拿到一个数据x， x 就是一个样本了。我们得到的模型叫f。 f 对 x 会做一个判断，这就是f(x)。y 是真实的结果

  • 🍉教程，还是以🍉为例

  • 比如 y 是西瓜，切开之后我们知道它好不好，y是真实的结果；而f(x)是我们一开始根据颜色、纹理圈、根蒂来判断瓜好不好，f(x)是判断的结果。

  • 我们肯定希望料事如神，希望判断得准，如何表达这个“准”？🤔

    希望$|f(\mathbf{x})-y|$ 小于一个很小的数$ \epsilon$。比如 $ϵ$为0.0001，就够准了。如果是0就绝对准确了

  • 我们希望得到这样判断很准的f，但并一定就能得到这样的f，于是引入概率，我们希望我们有较大的概率得到这样的f

    • 怎样表达这个较大的概率？
    • 这个概率大于等于$1-\delta$，如果这个$\delta$非常小，就意味着这个概率非常逼近于1。如果这个$\delta$ 是0，也就是意味着每次绝对能得到这样的f

思考两个问题

• 为什么是小于等于$ϵ$，为什么不应该去追求等于0？
• 为什么是一个概率的，概率再大，也不是每次绝对能拿到那样的结果，那为什么不追求每次绝对能拿到那样的f

回答这两个问题，首先要明白AI、ML在研究和解决什么样的问题

问题性质角度

• 机器学习研究的问题有高度的不确定性，高度的复杂性，而且我们甚至不知道怎么去做它。
• 例如要做一个故障诊断，假设我们已知故障诊断的一个指标是:温度高于 90 度，就会出故障。这就是一个确定性的规则/确定的知识/确定的公式。但是在很多问题上，我们没有这么清楚的知识。比如一个东西超过 90 度它会出问题，低于 90 度的时候它也会出问题。很多因素合在一起之后对它起作用，而这些因素到底怎么对它产生结果，我们不太清楚, 这时候我们才会去用机器学习。
• 当我们的知识已经不能够精确给出我们结果的时候，我们从数据里面去分析，希望从数据里面能帮助我们找出答案。这时候我就不能指望它是百分之百准确的，因为它不是那种我们清楚的了解的问题。

计算要求的角度

• 有一个著名的问题 P对NP问题

  “P/NP问题”，这里的P指多项式时间（Polynomial），一个复杂问题如果能在多项式时间内解决，那么它便被称为P问题，这意味着计算机可以在有限时间内完成计算；

  NP指非确定性多项式时间（nondeterministic polynomial），一个复杂问题不能确定在多项式时间内解决，假如NP问题能找到算法使其在多项式时间内解决，也就是证得了P=NP。比NP问题更难的则是NP完全和NP-hard，如围棋便是一个NP-hard问题。

• 我们现在机器学习会研究什么样的问题？

  • 比如: 谷歌搜索，提供一个查询关键词，返回搜索结果。
  • 能不能在多项式时间复杂度内给出最佳结果? 不能
  • 给一个查询，能不能在多项时间里面说明它是最优的？也不能。
  • 所以实际上我们经常处理的问题难度都已经在 NP 问题之外了。也就是我们经常做的问题，哪怕给出了解，在多项式时间里面验证解有多好, 都做不到。

---

• 再返回那两个思考的问题
  • 如果$1-\delta$是1，$ϵ$是0，也就意味着要求存在这样的问题:每一次运行都能得到确定的最佳答案。那实际上就构造性地证明了 p = np，甚至 p=np 之外的所有问题
  • 所以做不到 $1-\delta$是1，$ϵ$是0
  • 既然 0 和 1 做不到，就退一步，希望尽可能接近即可，以很高的概率得到一个很好的模型，就是概率近似正确

四.基本术语

• 数据集：我们拿到的所有数据构成的集合，就数据集。

• 训练：我们拿到的数据用来建立这个模型，建立这个模型的过程就是训练。

• 测试 test

  • 指拿到模型后，给一个新的数据，用这个模型去判断数据做对了还是做错了，其实就是 用这个模型。

  • 模型做好之后，想判断这个模型有多好，就拿另外一部分数据去提供给它来做测试。

    下面老师这里讲的挺好的哈哈。

    就比如老师给大家上课，上了一个学期之后，要考察大家学的好不好，最后要出一套考题，大家在这套考题上来做，最后老师来判断好不好。

    • 这样一个测试是为了了解模型的性能，所以这时候的测试数据，它的结果是知道的，这个卷子的答案老师一定是知道的，否则老师没法给学生评分
    • 同时测试为了得到一个比较客观的结果，这些题目老师应该一开始没有给过学生。不能说考试前一周所大家看，老师这有 30 道复习题，学生把这 30 道搞完了，最后考了 100 分，这是一个过于乐观的测试，并不代表学生真的学会了

  • 我们通常在测试的时候，测试数据和训练数据，应该是分开的

  • 测试是把模型拿来用，而这个用 既可能是考察模型好不好，也可能是输入一个东西，让模型给结果

• 示例（instance）、样例（example）

  example 是有结果的， instance 是没有结果的

  • 我们看表的第一行，前面部分是在描述它的输入部分，颜色怎么样，纹理怎么样。最后有一个东西是它的结果。
  • 示例只包括前面部分
    • 一个西瓜，颜色青绿色，纹理是清晰，根蒂蜷缩，这就叫示例。
  • 如果把这个瓜好不好也给出，这就叫样例

• 样本 Sample ， 比较模糊，需根据上下文来理解

  • 有时候我们说一条数据（表中的一行）是一个sample。
  • 有时候我们会说整个拿到的数据集是一个sample，因为拿到的数据集是所有可能的数据中的一个采样。我们把它叫做一个商铺。所以这要根据上下文来理解了。

• 属性 attribute 特征是feature

• 颜色是青绿色，这个颜色就叫一个属性（也把它叫一个特征），青绿色就是属性值（在属性上的取值）

• 特征向量； 属性空间/样本空间/输入空间

  
  • 把每一个属性想象成坐标上的一个轴，比如x轴是声音，y轴是颜色，z轴是根蒂
  • 这时候任何一个西瓜，如果用这三个属性描述，都是在这空间中的某一个点，从代数角度来看，这就是一个向量
  • 所以这时候我们把它叫做一个特征向量（feature vector）
  • 属性张成的空间，我们就把它叫做属性空间
  • 因为很每一个样本，所有的样本都是在空间中存在的，所以我们也称之为样本空间，或者输入空间

• 标记空间/输出空间

  • 西瓜这个例子只是 好瓜 这个轴
  • 但现实问题会比较复杂。比如如果我们多输出回归，每一个轴它都是一个实指，这时候输出（标记），也是一个向量。

• 假设（hypothesis） 真相 （ground-truth）

  • 模型
    • 所谓的模型，其实是找到了某种规律。
    • 比如现在要找到的是颜色是青绿色，耕地是蜷缩，敲起来声音很浑浊的这样的西瓜是一个好西瓜，就会得到了一个规则
    • 这个规则假设我们把它当做一个模型，实际上它是揭示了 关于 什么是好西瓜 的一个规律。
    • 模型揭示了关于我们要判断的结果的一个规律。
      • 这个规律可能是显式的，比如我们一看就知道颜色，青绿色
      • 也可能是隐式的。比如一个神经网络，看不清楚它在干什么，但是反正输入一个西瓜，它就能告诉你是好还是不好。
    • 所以模型包含了一个规律。而模型找出来的这个规律不一定是正确的，所以它实际上是形成了一种假设。
  • 当我们说 hypothesis 的时候，它其实就是在指我们学到的模型。对一个问题，我们可以形成很多的hypothesis，真的假设就是事实的真相（ground-truth）。
    • 比如我们要学习的是“青绿、蜷缩、浑浊是好西瓜“。这一条，它就是 ground-truth，是一个正确的答案。
    • 模型学到了一个东西，而这个东西是关于结果的一个可能的规律，这个规律不一定对。如果它是对的，就是真相。
  • PAC模型中，f(x)就是hypothesis， y 就是 ground-truth

• 学习器（learner）

  • 此门课程中，学习器可以认为是学到的模型，（从学习的过程的角度来考虑模型，当一个学习算法，我们给定了它数据和参数设置，这时候产生出来模型），可以认为学习器是一个学习算法，它对一个数据和一个参数，在给定示例之后，得到一个结果
  • 或者粗糙理解：刚才我们说一个分类的模型叫分类器，回归的模型叫回归器，这个地方叫学习器

关于输出部分的术语

• 分类（classification）；回归（regression）

• 分类是离散的输出，回归是连续的输出

• 二分类，多分类

  • 二分类是我们研究的最基本的问题，因为所有的多分类问题，我们可以把它分解成若干个二分类问题。

    此门课，大多数算法都是以分类，特别是以二分类为一个典型的例子。

    别的问题都可以把分类问题进行扩展，得到它类似的结果。

• 正类，反类

  在二分类里面，我们涉及到两类样本，好西瓜和不好的西瓜。我们通常会说有一类是正类，有一类是负类。但是大家注意，正类是不是一定是指好西瓜？不一定。也可以把坏西瓜当成正类，它只不过是对这个类别 a 和 b 抽象出来的一个说法，抽象出来是 a 是正， b 是负，或者 a 是负， b 是正。

  • 通常假设这两类是可交换的。这个假设非常重要。
  • 可交换意味着这两类它满足的分布和它的很多性质是差不多的。
    • 比如至少你在数据集里面，这两类的比例差不多。比如 100 个数据，你 50 个是a， 50 个是b，你a、 b 正负可以交换。但是如果有一类特别多，另外一类特别少，这时候你交换之后，性质就发生变化了。

还有几个术语是关于我们考虑的学习任务

• 监督学习（supervised learning）；无监督学习（unsupervised learning）

  监督学习有时候又把它叫做有导师的学习，无监督学习有时候叫无导师学习

  • 输出结果不知道的，就是无监督学习。

  监督学习，有很多西瓜，有很多好的坏的，我判断以后的西瓜是好的坏的

  如果无监督学习，给我一堆西瓜，好的坏的都不告诉我，我这能做什么？难道我还能判断什么是好，什么是坏吗？你连好坏是什么都没告诉我，显然我不能判断好坏了。这时候我能怎么做？

  我可能能做的是把这些西瓜分成很多堆，这边有一堆，我可能根据颜色分成很多堆，根据产地分成很多堆，根据大中小分成很多堆，这就是在做一个聚类。分成很多堆之后，你以后可能再做进一步的处理。这样的东西就是在做非监督学习。

  • 监督学习的典型任务：预测类任务，分类回归
  • 非监督学习的典型任务：离散类别，做聚类
    • 我们把数据分成若干个离散个类别
    • 也有可能处理连续的，做密度估计

• 未见样本（unseen instance）

• 机器学习要处理的是未来的新数据。做好模型不只是把训练数据做好，还要把未来做好

• 未知分布

  • 我们有一个基本的假设，我们拿到的所有数据都来自一个潜在的分布。

  • 我们实际上是假定了数据背后有一个规律，我们看到的所有数据都是根据这个规律抽出来的

  • 只不过我们的训练数据是从所有里面得到的这么一部分，而以后要判断的东西同样也是整个符合规律的数据里面抽取来的。所以把整个分布把握的比较好了，新的东西就能处理好了。这是机器学习的基本假设。

  • 所以绝不是未来随便给什么东西都能做。是假设未来要处理的和原来的数据是来自一个分布，一个distribution，而这个分布是什么并不知道。我们把它叫做未知分布。

• 独立同分布（i.i.d， identical and independent distribution）

  • 我们要一个重要的假定，所有的数据都是从分布来的，我们把它叫做独立同分布数据

  • 每个样本他们都是独立的，从同一个分布产生的。

  • 如果不满足这条假设，机器学习就不能利用概率统计提供的工具了

  • 只有我们认为每一个样本都是独立同分布取出来的，这样我们的每一个样本，你可以把它看成是一个独立随机事件，才能够用独立随机事件出现的频率去逼近它的概率。

    • 如果我们都不能够假定样本是一个独立同分布，不能假定每个样本是独立随机事件，那么从统计来推断它原来概率分布这个工具本身就要打问号了，会给我们带来巨大的障碍。

    • 现在基本上做的所有的学习，都有独立同分布的假设。

    • 但是考虑这个现实问题，好像不能基于独立同分布的假设来建模

      • 比如第一个客户在淘宝买了一个帽子，第二个客户在淘宝买了一个珠宝，他们真的是独立同分布吗？他们不一定独立，第一个人可能是第二个人的朋友，第二个人是因为第一个人告诉他可以在淘宝买，他才去的。

    • 那么怎么突破独立同分布的假设？这是机器学习里面最前沿的研究内容之一，要引入一些现代的数学技术，入门性的课程，大家知道这些事情在做的是可以做的就ok

      • 就是怎么。而这里面往往，或者是对原来的概率统计技术的一个改变。而作为我们一个。但是作为基础，你还是要从独立同分部开始。也就是我们现在看到每一个样本，你可以认为它是个独立随机事件。

• 泛化（generalization）

  • 学到的模型处理新数据的能力越强，我们说它的泛化能力越强，可以把它理解为推广。
  • 泛化术语，对应的术语叫specialization，特化（从一般到特殊）。
  • 我们经常会强调一个模型的泛化性能。就是模型对新数据处理的能力有多好，以后我们关心的重点就是怎么样得到一个对新数据处理能力非常好的模型。
  • 在PAC模型中，所谓泛化，实际上指的就是$ϵ$到底能达到多小。理论上说，有时候我们要推一个泛化界，就是$ϵ$到底能够有多小，最好能够做到什么程度
    • 如果发现最好做到的结果是无限差，就说明这件事根本不可能用机器学习去解决它。
    • 所以机器学习的基本理论会告诉我们什么事情是不可以做的。比如泛化在这个问题上，最好情况下误差不会小于50%，你就知道了不值得做。但是如果最好可能做到0.2，你可以努力去设计有效算法。并不是一定能做到，但是如果你设计有效算法，可能做得到。
    • 所以这是理论会带给我们的指导，告诉我们什么是不能做的，还有什么东西通过努力，你可能能做到一个什么程度。

五.归纳偏好

• 归纳偏好（inductive bias）

• 机器学习算法在学习过程中必定需要有某种类型的偏好，叫归纳偏好。

  有的地方bias翻译为偏置

• bias表达的就是对某一种东西有特别的喜好

• 考虑一个简单的情况，现在只有两个两种可能，一种是A，一种是B。实际上对一个具体的学习算法，当这两者都完美的解释了训练数据的情况下, 它要做的考虑就是 A和 B 到底哪个更好。

• 任何一个机器学习算法必须有它的偏好。

• 当这样的情况出现的时候，选择 A 还是选择B，这就导致了算法的不同。

  • 虽然形式上可能有很大的差别，比如有的是个决策树，有的是个神经网络，有的是个支持向量机。
  • 但本质上它是需要做出某种选择。这种选择是他相信什么样的模型/假设是更好的

• 基本准则是什么？ 奥卡姆剃刀

  • 基本想法：若非必要，勿增实体
    • 简单来说，当我们发现有很多的假说都能够完美的解释我们的观察，这时候我们就选最简单的

• 机器学习里面我们看到的训练样本，可以认为这就是我们看到的现实的世界。而我们如果有多个模型都能很好的解释训练样本/现实世界 反映出来的现象，我们就找最简单的模型，这就是基本思路。

  • 比如上图那个问题，我们很可能就要找 A这条曲线，因为A更平滑更简单，如果我们要把它的函数方程式写出来，它的阶数可能更低，我们认为它更简单，所以我们很可能就取它了。

  • 这个思想在整个机器学习里面是非常重要的一个思想。很多算法在进行取舍的时候，通常认为更平滑的、更 smooth 的东西是好的，而变化得更极端的东西通常不太好。 而背后的思路其实就是奥卡姆剃刀

  • However，找出最简单的模型这件事情本身并不简单，利用“奥卡姆剃刀”原则时，确定哪个假设更“简单”，这个问题本身不是简单的。

    • 以曲线方程为例 ：$y=a{x}^2+bx+c$ 和 $y=a{x}^3+c$
      • 从阶数角度可以说前者更简单，从参数数量角度可以说后者更简单
      • 到底哪一个更简单？所以这本质上不是个简单的问题。

    所以在机器学习里面，特别是我们涉及到不同模型的时候，它背后形成的假设，关于”什么是更简单的“是不一样的，是不容易下判断的。

• 虽然心里面有这么一条简单的准则，但是这条准则当你实际上要发挥的时候，变化很多，所以这就导致机器学习里面会有那么多的算法，这些算法都在采用不同的假设，不同的偏好

• 很多人会问，什么样的算法比较好。这个问题里最关键的一点是 学习算法的归纳偏好是不是和问题本身匹配，这实际上决定了算法在任务上到底能用得多好。

  • 真正 work 的不是算法，而是背后的假设是什么，偏好是什么，偏好是不是和现在问题合适。
  • 比如我们要考虑一个故障诊断问题，如果故障是很长时间都不会太出现的，A和B都对，我们可能会取A。如果有一个东西，它是非常频繁的发生变化的，可能这时候我们应该取B。
  • 什么样的偏好和当前这个问题更匹配。我们必须要对问题有一个清楚的认识。

• wiki上关于奥卡姆剃刀：

  奥卡姆剃刀（英语：Ockham’s Razor、拉丁语：Lex Parsimoniae，意为“简约法则”）是由14世纪方济会修士奥卡姆的威廉（William of Occam，约1287年至1347年，英格兰萨里郡奥卡姆 (Ockham)人氏）提出的逻辑学法则。换言之，如果关于同一个问题有许多种理论，每一种都能作出同样准确的预言，那么应该挑选其中使用假定最少的。尽管越复杂的方法通常能做出越好的预言，但是在不考虑预言能力（即结果大致相同）的情况下，假设越少越好。

  所罗门诺夫的归纳推理理论是奥卡姆剃刀的数学公式化：[1][2][3][4][5][6]在所有能够完美描述已有观测的可计算理论中，较短的可计算理论在估计下一次观测结果的概率时具有较大权重。

  在自然科学中，奥卡姆剃刀被作为启发法技巧来使用，更多地作为帮助科学家发展理论模型的工具，而不是在已经发表的理论之间充当裁判角色。[7][8]在科学方法中，奥卡姆剃刀并没有被当做逻辑上不可辩驳的定理或者科学结论。在科学方法中对简单性的偏好，是基于可证伪性的标准。对于某个现象的所有可接受的解释，都存在无数个可能的、更为复杂的变体：因为你可以把任何解释中的错误归结于特例假设，从而避免该错误的发生。所以，较简单的理论比复杂的理论更好，因为它们更加可检验。[9][10][11]

六.NFL定理

哪个算法更好？

• 我们有两个算法的时候，我们能不能说谁比谁更好？

• 还是用前面的A和B那幅图举例，我们拿到 5 个训练数据点黑点。现在有两条曲线，把它们都穿过去，都完美的穿过去。从训练数据上来看，他们一致了。

  • 我们现在问 A和B 谁更好

  • 我们说最简单的，最平滑的好，因为很可能像左上图的情况，正好完全穿过去未来的数据测试样本的，所以 A 更好， B 不太好。

  • 但是也有可能是右上图的情况，恰好这些测试样本点还真的没有出现在 A 上，它都出现在 B 上面了，这时候 B 好像更好。

  • 左上图的可能性大，还是右上图的可能性大，很难判断。也有时候 A 算法好，有时候说 B 算法好

  • 这个结论到底是个巧合，还是一个必然的结果？

• 机器学习里有一个非常重要的定理，没有免费的午餐 NFL(no free lunch）

  • NFL定理 : 一个算法 ${\mathfrak{L}}_a$若在某些问题上比另一个算法 ${\mathfrak{L}}_b$ 好，必存在 另一些问题 ${\mathfrak{L}}_b$ 比 ${\mathfrak{L}}_a$ 好

NFL定理的寓意

• 两个算法，如果我们说有些问题上 A 是比 B 好的，一定存在另外一些问题 B 是比 A 好

• 很多东西都可以说是一个算法吗？

  • 比如：任务是分类。
    • 随机猜测也是一种算法，来一个，瞎蒙一个yes。再来一个，猜一个NO。随机蒙。这也是个算法。
    • 此时有个非常巧妙设计的算法，在有些问题上比随机瞎蒙好，但是我有一些问题随机瞎蒙反而更好，

• 在现实中做机器学习的时候，一定是要对一个具体的问题来考虑。只要在当时考虑的问题上做得好就行了

• 下面老师举的例子好玩哈哈哈

  • 比如出行的考虑，我就告诉你我们去新街口，我们用什么算法好？第一个算法是坐飞机，第二个算法是骑车。这两个算法一样好。去北京新街口坐飞机好，南京新街口骑车好。

• 一定要有非常具体的一个问题，我们才能谈得出算法的好坏，否则没有差别。**脱离具体的问题，空泛的去谈什么学习算法更好，是没有任何意义的。**可能在你的问题上非常好的算法，恰恰是大家认为非常拙劣的一个算法。也完全有这种可能，大家现在都公认很好的算法，在你的问题上可能恰恰不work。那么有一些流行的算法， 他们其实是在比较多的问题上表现得比较好，但是绝对不是所有的问题它都做得好。而在实际应用的时候，你往往考虑的就是你特殊的问题。所以一定要具体问题具体分析，只有在你知道你要解决的问题是什么的情况下，才谈得上我们去考虑什么算法对这个问题更合适。

• 当我们谈到”问题时“，一定要清楚， x （输入空间）是什么， y（输出空间） 是什么，输入和输出空间都确定了，这才是一个问题。如果不谈x，不谈y，只是去泛泛地说，分类也好，推荐也好，这对我们搞机器学习的人来说，这还不是一个问题。

  比如一般人理解分类就是个问题，推荐就是个问题，我做推荐，你告诉我什么算法好。但是在机器学习中，这还不叫一个问题，因为没有确定输入输出。比如推荐，在腾讯推荐游戏和在淘宝推荐衣服，这就是不同的问题。因为用来刻画它的属性是完全不一样的，这就意味着获得的数据，它的数据分布是完全不一样的。而不同的数据分布上，建模可能用到的技术需要不一样。

现实机器学习应用

• 机器学习学什么呢？

• 很多人谈机器学习，一开始就会说，有没有把机器学习的很多算法学会。很多机器学习书籍会介绍很多算法，这就会给人一个感觉，从机器学习里面是不这些算法很多种算法，这样我把每种算法都搞熟悉了不就好了。但是其实有了刚才认识大家，你就要知道了，所谓的一些”十大套路“，”二十大招数“其实就是一些基本的招数和套路。

• 比如就说 10 个算法， no free launch 告诉我们，对每一个算法一定有它非常不擅长的问题。不擅长的问题，绝不可能全部被这 10 个算法全部覆盖了？。我们现实世界里面碰到的各种各样的无穷无尽的问题，用有限数目的算法去应对无限的问题，肯定在大多数时候是不好的。

• 当我们来一个新问题的时候，我们更需要的往往是按需设计，度身定制。这个问题的特点可能是以往的算法都没有真正考虑过的。根据这个特点，专门为设计出一个东西来，这对新的问题来说可能才是最好的解决方案。

  • 下面这段话老师说的也好有意思哈哈哈

    就好像你降龙十八掌这个东西也不行，打狗棒法也不行，但是我们大家为什么要学习？你把他们的精华学到了，你说我用降龙十八掌的思想，使出了一招打狗棒法，这时候迎刃而解了。其实是这样的，我们有时候经常在解决一些问题的时候，我们跟企业有很多合作，企业的工程师说周老师，你们最后是用什么算法来解决这个问题的？其实我很难说这不是一个存在的算法，它可能是用到了一个神经网络的形式，可能用到了支持向量机里面对某个问题的一种理解，还有可能用到了决策树对整个方法，它的一个思想方式，这几个东西它的一个结合。其实你可以认为这有点像这种无招胜有招的结果，但是在一开始你一定要把这些招数搞明白，这时候你才有可能在打狗棒法里面把降龙十八掌的含义掌意把它使出来。

    所以大家知道，在一开始学习的时候，你要把这些套路学一学，但是到最后解决问题的时候，我们这一行最重要的是按需设计，度身定做。所以有时候我们就像裁缝一样，做最好的衣服，一定是根据你的每一个人，他的身形量出来再做的。但是如果没有这么多钱请高明的裁缝就只有到商店里面去买成衣。别人已经做好的一套一套的工具，大号中号、小号你试一下，稍微差不多就穿走。但这可能已经不是最好的解决方案了。

• 这个NFL定理真的值得好好思考！

  老师后面举的例子也很引人深思哈哈哈，大学前两年的学习很多很多时候流于浮躁，没有踏实地去学习这个学科的一些基础知识和固有套路， 最近意识到应该认真去看一些计算机的经典书籍和课程，这方面很重要！

  没有扎实的基础，是真的”无招“， 有基础，才能做到”无招胜有招“

参考资料

• 西瓜书🍉
• MOOC
• CSDN大佬博客