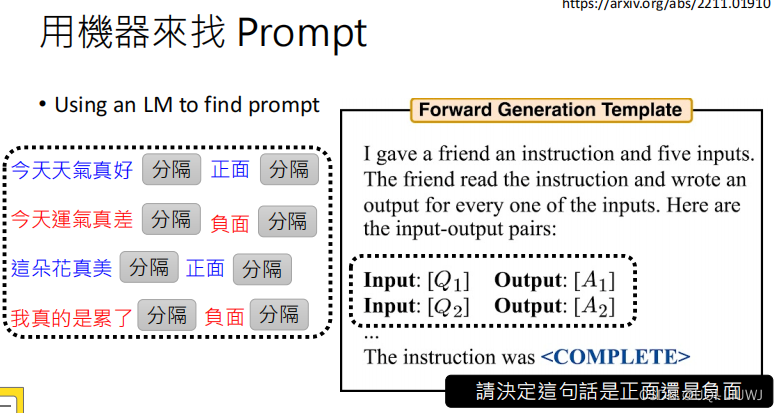
参考2023牛客暑期多校训练营6(G、E、C、B、A) - 知乎 (zhihu.com)
纯数学,推式子
从贡献度的角度考虑
首先,当两个子集大小均相同时,才有可能变相同
其次是我们需要先将S和T中的数分别从小到大排个序,然后要变相同花费最小,肯定是对齐的数之间变换,可以举个例子感受一下,然后直接记结论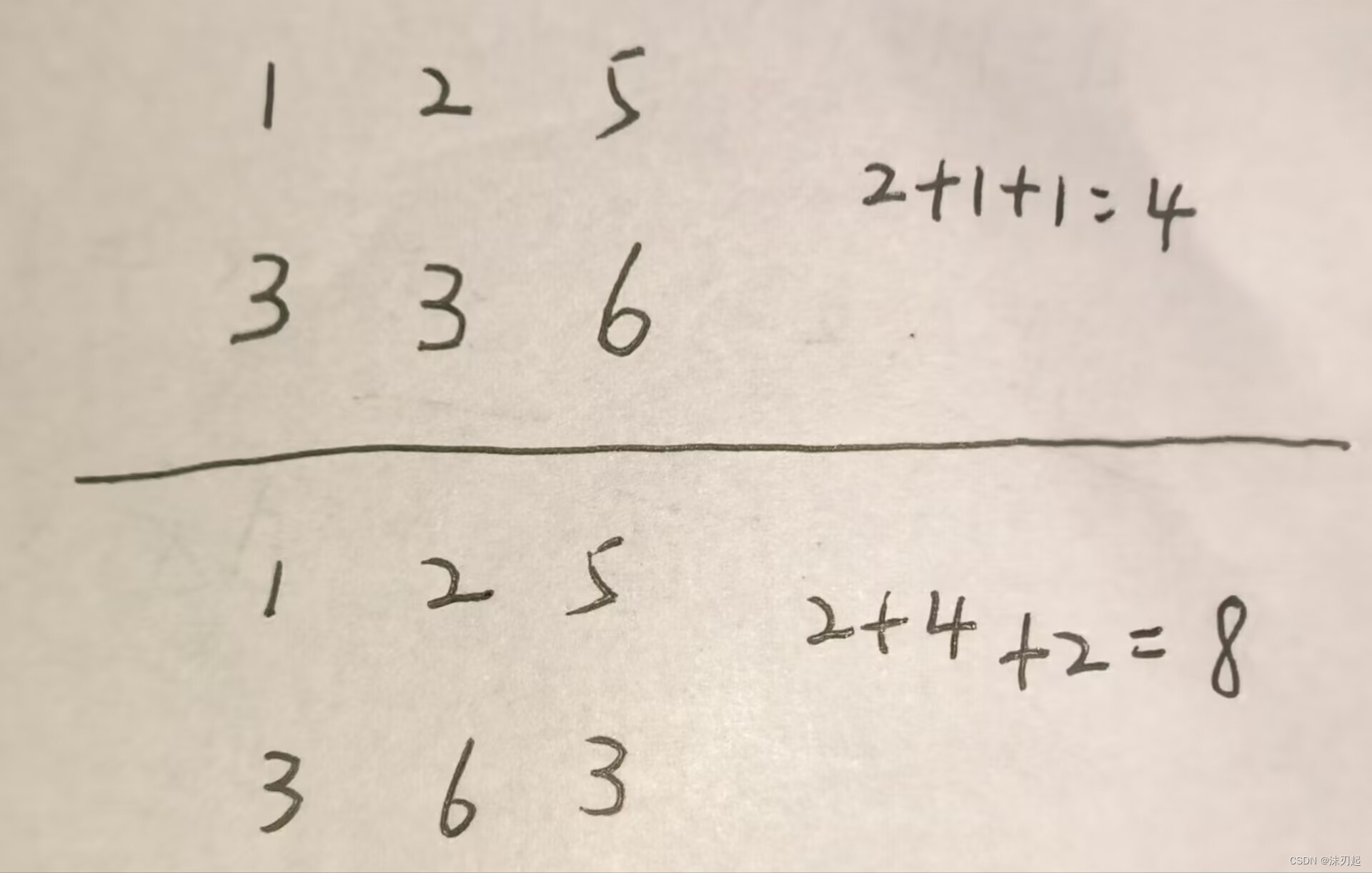
我们从S中找一个数Si,从T中找一个数Tj,它们作为1对,分别放入A和B中,然后它们的贡献度即为它们之间的差的绝对值乘包含这一对数的组合数(即符合条件的包含这一对数一共有多少种排列组合,保证Si时A中第x大的数,Tj也是B中第x大的数,这样对齐了,算的才是变成相同的最小花费),然后我们只要将每一对数的贡献度全部加起来即可
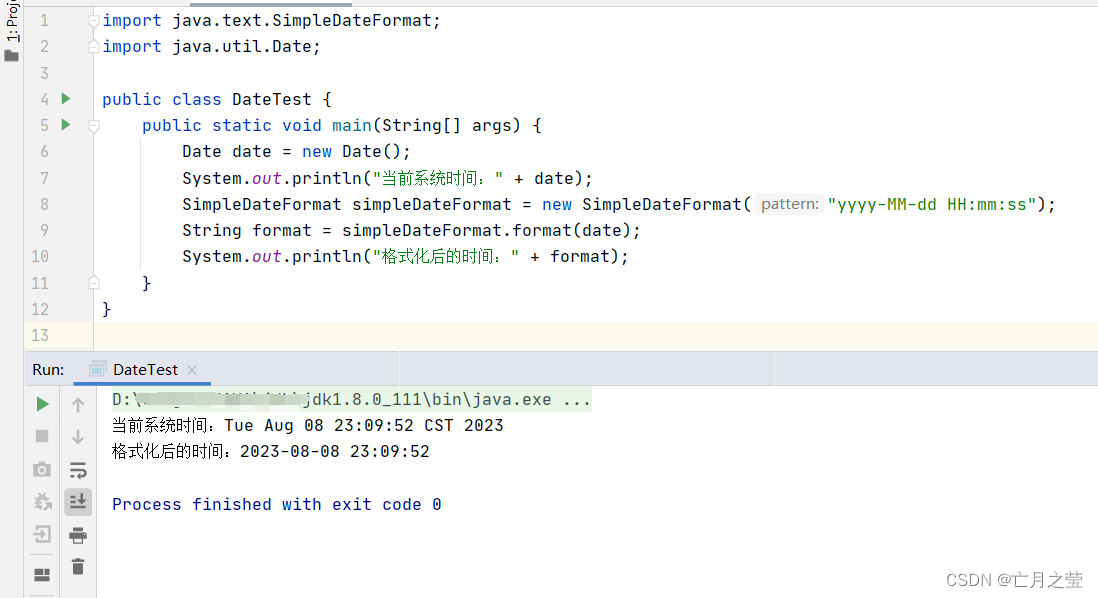
现在的关键就是如何求组合数,我们这样考虑,假设我们找了Si,Tj这样一对数,首先需要保证它们分别是A中第x大的数和B中第x大的数,现在我们要做的是在S中选择x-1个小于Si的数放在A中,在T中选择x-1个小于Tj的数放在B中,然后就是在S中选择y个比Si大的数放在A中,在T中选择y个比Tj大的数放在B中
我们只要枚举x从0到min(i-1,j-1),枚举y从0到min(n-i,n-j),就可以列举出所有情况,将全部的组合数加起来就可以了
即
![]()
但是这样的话,每次求组合数都是O(n),肯定会超时,我们需要设法通过变形使得求组合数为O(1)
我们设函数g(i,j),有
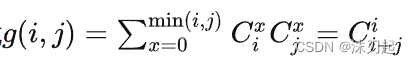
可以这样理解:我们有i个红球,j个蓝球,我们要不管颜色地从中选取i个,即C(i+j,j),然后我们也可以这样选,就是从j个蓝球中选x个,从i个红球中选取i-x个,这样的话,就是C(i,i-x)*C(j,x),然后我们枚举x从0到min(i,j),就是所有情况,加起来就相当于不管颜色地从i+j个球中选择i个(为什么不是写C((i+j),min(i,j),因为C(i+j,i)等于C(i+j,j),所以无所谓是i还是j)
所以最后组合数就是
![]()
对于快速求组合数,我们可以先预处理阶乘和阶乘的逆元
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
#define int long long
using namespace std;
typedef long long ll;
const int N=4e3+10,mod=998244353;
int s[N],t[N];
int fac[N],ifac[N];
int n;
int qmi(int a,int k){
int res=1;
while(k){
if(k&1) res=(ll)res*a%mod;
a=(ll)a*a%mod;
k>>=1;
}
return res;
}
//求组合数
int C(int n,int m){
if(n<m) return 0;
return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
void solve()
{
cin>>n;
fac[0]=ifac[0]=1;
for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod;//预处理阶乘
ifac[N-1]=qmi(fac[N-1],mod-2);
for(int i=N-2;i>=1;i--) ifac[i]=1ll*ifac[i+1]*(i+1)%mod;//预处理阶乘的逆元
for(int i=1;i<=n;i++) cin>>s[i];
for(int i=1;i<=n;i++) cin>>t[i];
sort(s+1,s+1+n);
sort(t+1,t+1+n);
int res=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
res=(res+abs(s[i]-t[j])%mod*C(i-1+j-1,i-1)%mod*C(n-i+n-j,n-i)%mod)%mod;
}
}
cout<<res<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}C.idol!!
大致题意是给你一个n,然后求出1!!*2!!*...*n!!末尾有几个0
数学知识,先推式子
发现只有2和5相乘能得到1个0,所以问题就就转换成了有几对2,5组合,但是由于因子5的个数肯定少于因子2的个数,所以我们只要算出因子5的个数即可
n可达1e18,然后又是双阶乘,5的个数肯定会爆long long,所以我们考虑使用更大的数据类型__int128,但是使用__128int需要自己手写输入输出函数
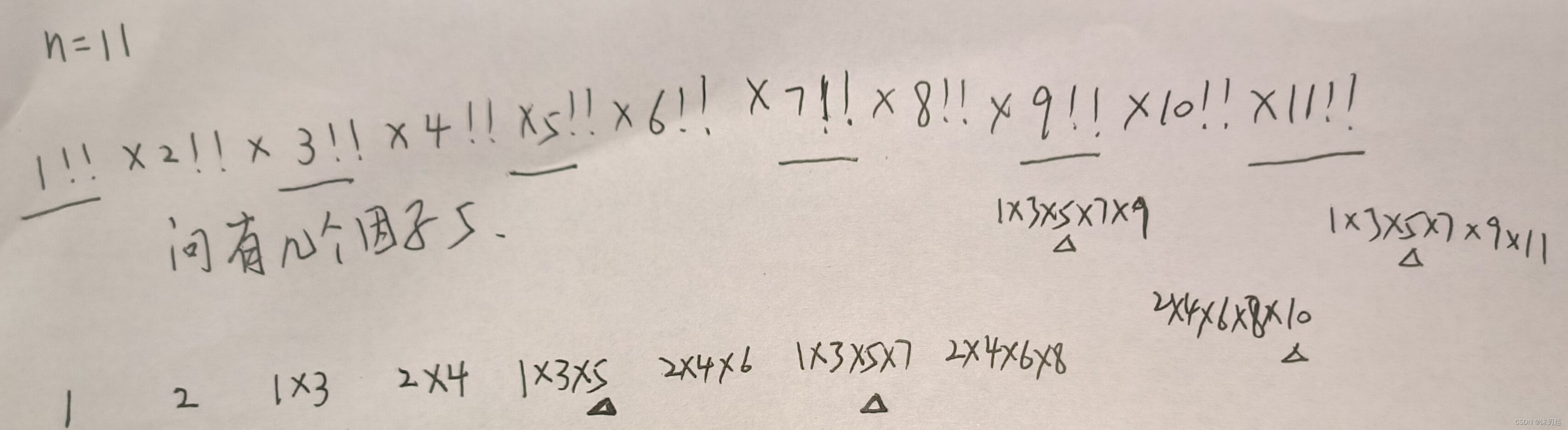
我们先考虑样例,n为11时,我们分奇偶来看,当为奇数时,就看因子5的个数,当为偶数时,就看因子也看因子5(10可分解为5*2,也有因子5)的个数,故末尾一共5个0
奇偶分开来考虑:
对于奇数,我们会发现,从5开始,即5!!,7!!,9!!,....
每5个数贡献度+1
比如说
5!!=1*3*5,7!!=1*3*5*7,9!!=1*3*5*7*9,11!!=1*3*5*7*9*11,13!!=1*3*5*7*9*11*13,这5个数贡献度均为1;
15!!=1*3*5*7*9*11*13*15,.....19!!=1*3*5*7*9*11*13*15*17*19,这5个数贡献度均为2
比如说当n为31时,每5个数贡献度+1,所以我们就算出这些数的贡献度,即5个1,5个2,4个3,如何算呢?可以先算出整个区间的长度,len=(n+1)/2-(i+1)/2+1;其中n为31,(n+1)/2即代表31!!所在的下标,i表示每几个数贡献度+1,此时等于5,(i+1)/2表示5!!的下标,两下标相减再加1即表示区间长度,然后以每5个数为一个周期区间,算出n所在的周期区间不算,然后前面有几个完整的周期区间,maxn=(len-1)/i,然后len*(maxn+1)-i*maxn*(maxn+1)/2就是用len*3减去一个等差数列求和,得到每5个数加1得到的所有数的贡献度
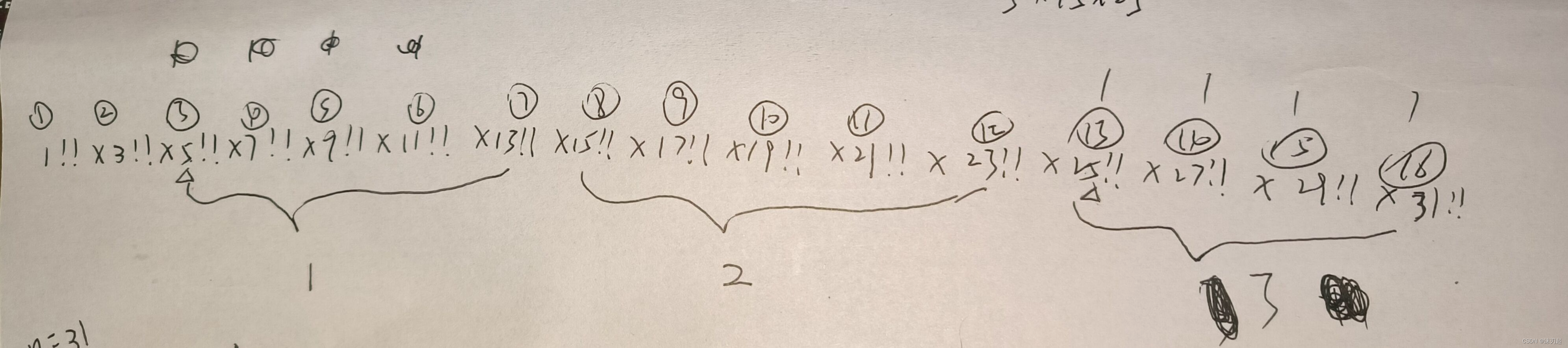
但是,这样还远远不够,因为我们发现25的贡献度并不只是3,25=1*3*5*7*9*11*13*15*17*19*21*23*25,发现贡献度为4,它是在贡献度为3的基础上加了1,也就是说每25个数,它会在原来贡献度的基础上再加个1
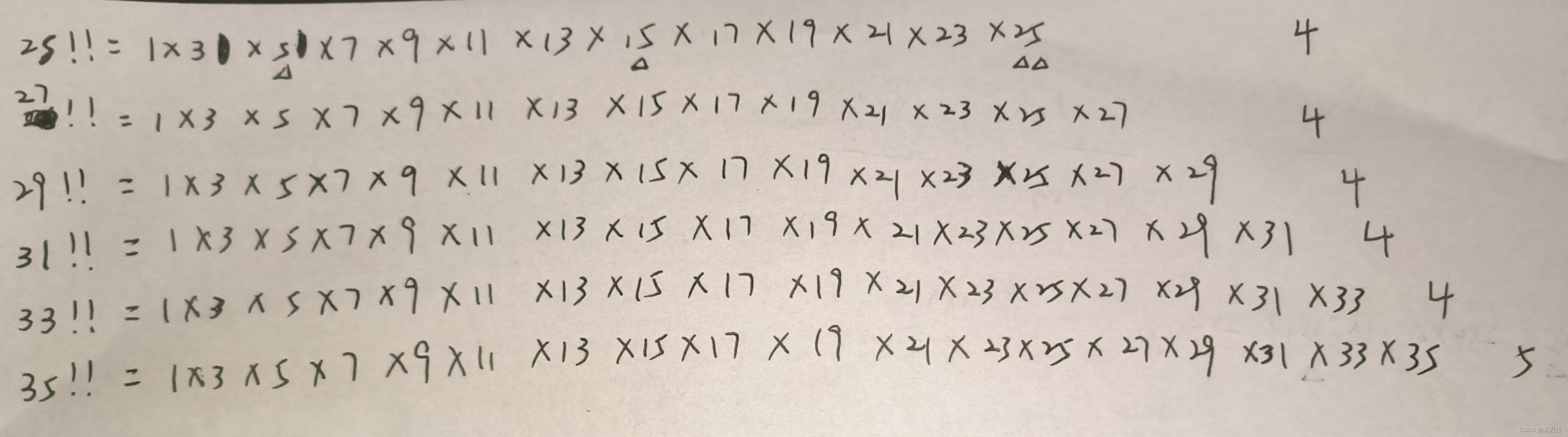
然后同理,每125个数,它会在原来贡献度的基础上再加个1,以此类推,5的幂次...
所以总结下来就是:每5个数贡献度加1,每25个数贡献度加2,每125个数贡献度加3...,但由于算每5个数贡献度加1的时候已经给25和125加1了,所以算每25个数也是贡献度加1,由于算25个数贡献度也给125加1了,所以算每125个数也是贡献度加1,以此类推...
对于偶数,同理,我们会发现,从10开始,即10!!,12!!,14!!,....
也是每5个数贡献度加1,每25个数贡献度加2...
所以同理,只需在i的基础上乘2,再以同样的方法算贡献度即可
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<cstdio>
#define endl '\n'
#define int __int128
using namespace std;
typedef long long ll;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
inline void print(int x){
if(x<0) putchar('-'),x=-x;
if(x>9){
print(x/10);
}
putchar(x%10+'0');
}
int n;
void solve()
{
n=read();
int res=0;
for(int i=5;i<=n;i*=5){
int len=(n+1)/2-(i+1)/2+1;
int maxn=(len-1)/i;
res+=len*(maxn+1)-i*maxn*(maxn+1)/2;
int j=i*2;
if(j>n) break;
len=n/2-j/2+1;
maxn=(len-1)/i;
res+=len*(maxn+1)-i*maxn*(maxn+1)/2;
}
print(res);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}E.sequence
大致题意是能否把区间[l,r]分成k段,使得每一段的和均为偶数(有q次询问)
我们需要先预处理每个区间最多能分成几段区间保证区间和均为偶数
法一:
如果是偶数的话,完全可以自己作为一段区间,但是如果遇到奇数的话,就得至少到下一个奇数,这一整段作为一个区间
这里我们考虑奇数个数前缀和以及偶数个数前缀和

如上图,区间的分法一共有两种
一种是从第一个奇数到第二个奇数作为一个区间,第三个奇数到第四个奇数作为一个区间,..,未包含在以上区间的每个偶数单独作为一个区间,用数组x来单独处理第一种分法的有效偶数个数前缀和(具体操作是,先将有效的偶数记为1,再跑一遍前缀和)
另一种是从第二个奇数到第三个奇数作为一个区间,从第四个奇数到第五个奇数作为一个区间,...,未包含在以上区间的每个偶数单独作为一个区间,用数组y来单独处理第二种分法的有效偶数个数前缀和(具体操作是,先将有效的偶数记为1,再跑一遍前缀和)
只有这两种预处理能使得区间分的段数最多
然后再预处理一遍奇数个数前缀和
然后就是q次询问,对于每一个区间[l,r],如果奇数个数为奇数,那么不可能分成都是偶数和的k段,return no
如果区间长度小于k,return no
然后看区间[l,r]前面有即个奇数,即z[l-1],如果前面奇数的个数是奇数,我们就采用第二种分法,否则就采用第一种分法(从图中很容易看出)
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10;
const string yes="YES",no="NO";
ll a[N];
int x[N],y[N],z[N];
int n,q;
string query() {
int l,r,k;
cin>>l>>r>>k;
if((z[r]-z[l-1])%2==1||r-l+1<k) return no;
if(z[l-1]%2==1) {
ll res=(z[r]-z[l-1])/2+y[r]-y[l-1];
if(k<=res) return yes;
} else {
ll res=(z[r]-z[l-1])/2+x[r]-x[l-1];
if(k<=res) return yes;
}
return no;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--) {
cin>>n>>q;
for(int i=1; i<=n; i++) cin>>a[i];
for(int i=1;i<=n;i++) x[i]=y[i]=0;
//预处理奇数个数前缀和
for(int i=1; i<=n; i++) {
z[i]=z[i-1];
if(a[i]%2==1) z[i]++;
}
// for(int i=1;i<=n;i++) cout<<z[i]<<" ";
// cout<<endl;
int flag=1;
for(int i=1; i<=n; i++) {
if(a[i]%2==1) {
flag=1-flag;
continue;
}
if(a[i]%2==0&&flag==0) y[i]=1;
else if(a[i]%2==0&&flag==1) x[i]=1;
}
//预处理偶数前缀和个数
for(int i=2; i<=n; i++) x[i]+=x[i-1],y[i]+=y[i-1];
// for(int i=1;i<=n;i++) cout<<x[i]<<" ";
// cout<<endl;
// for(int i=1;i<=n;i++) cout<<y[i]<<" ";
// cout<<endl;
// for(int i=1;i<=n;i++) cout<<z[i]<<" ";
// cout<<endl;
while(q--) cout<<query()<<endl;
}
return 0;
}
法二:
用数组b记录前缀和,用数组c记录每一个位置已经有多少个偶区间了
同法一,如果该区间前面偶区间的个数为偶数,那么就选择第一种选法,否则就选择第二种选法
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const string yes="YES",no="NO";
const int N=1e5+10;
ll a[N];
int n,q;
ll b[N],c[N];
string query(){
ll l,r,k;
cin>>l>>r>>k;
if(r-l+1<k) return no;
if((b[r]-b[l-1])%2==1) return no;
if(b[l-1]%2==0){
if(c[r]-c[l-1]>=k) return yes;
}
else{
if(r-l+1-(c[r]-c[l-1])>=k) return yes;
}
return no;
}
void solve()
{
cin>>n>>q;
for(ll i = 1; i <= n; i ++ ) {
cin >> a[i];
b[i] = a[i] + b[i - 1];
if(b[i] % 2 == 0) c[i] = c[i - 1] + 1;
else c[i] = c[i - 1];
}
while(q--){
cout<<query()<<endl;
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}
G.Gcd
可以将a-b插入集合中,然后会不断地将集合中的两个数拿出来相减,再放回集合中,这让我想到了辗转相减法,是为了求两个数的最大公约数的
关于数学的题目,就用数学去推式子
有d=gcd(a,b)
假设a=k1*d,b=k2*d,a-b=(k1-k2)*d,得到的是d的倍数,之后每次取出两个数相减,也都是可以提取公因数d的,得到的始终是d的倍数,也就是说我们只能得到gcd(a,b)的倍数(可以用正数减负数得到更大的数)
然后对z为0时特判,题目说不能操作两个一样的数,所以当z为0时,a,b至少一个为0才可以
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
#define int long long
using namespace std;
typedef long long ll;
int x,y,z;
const string yes="YES";
const string no="NO";
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
string solve(){
cin>>x>>y>>z;
if(x==z||y==z) return yes;
if(z==0) return no;
int d=gcd(x,y);
if(z%d==0) return yes;
return no;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--)
cout<<solve()<<endl;
return 0;
}







![【LeetCode】数据结构题解(10)[有效的括号]](https://img-blog.csdnimg.cn/8053b819151947b7ad416333e3019636.png)