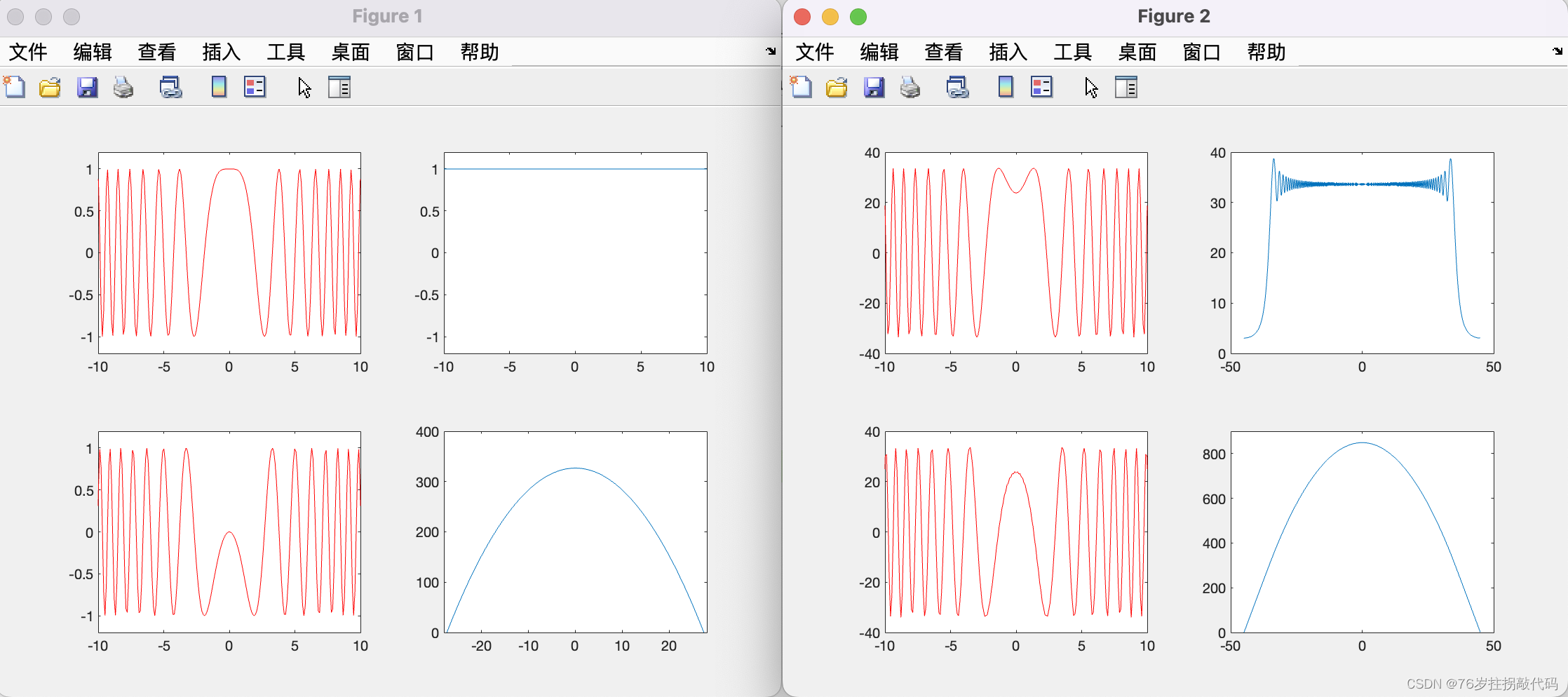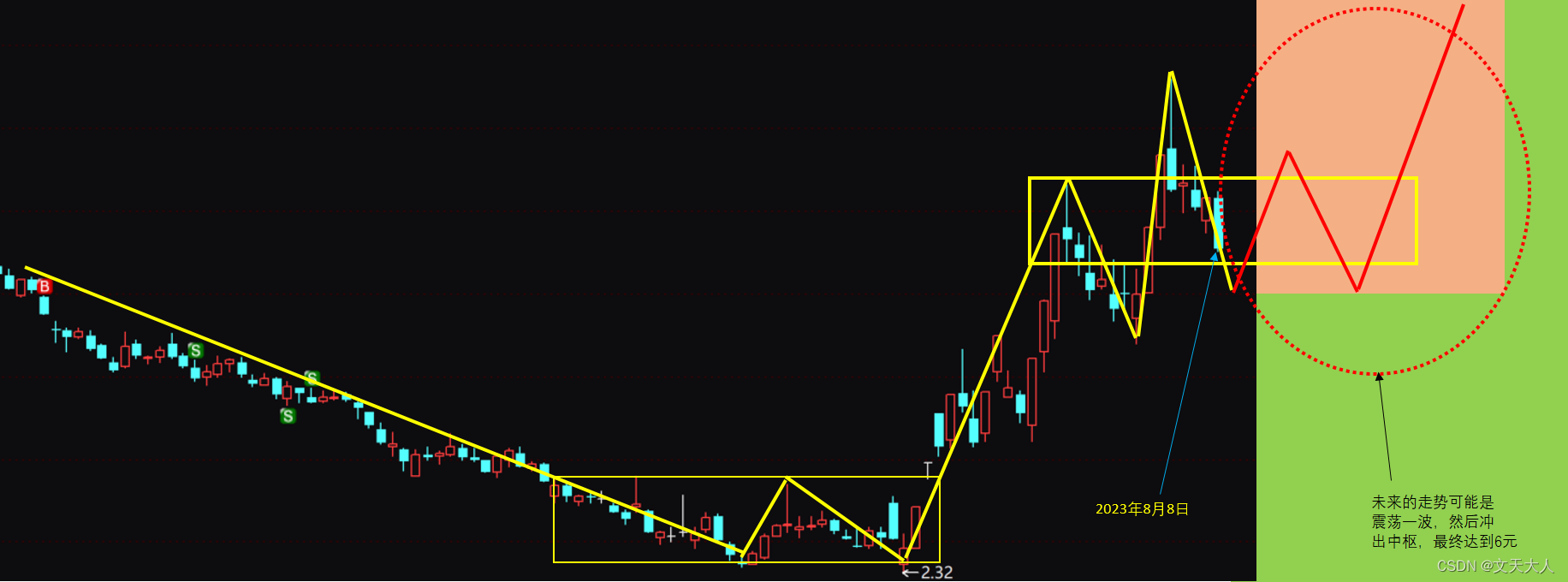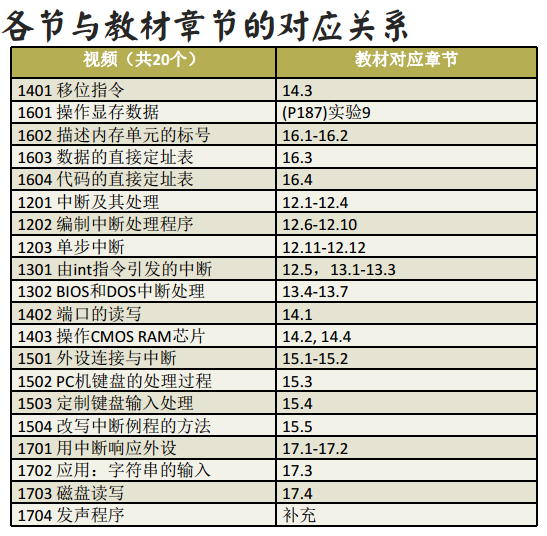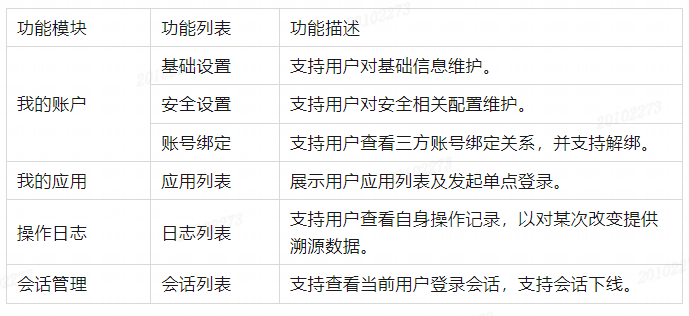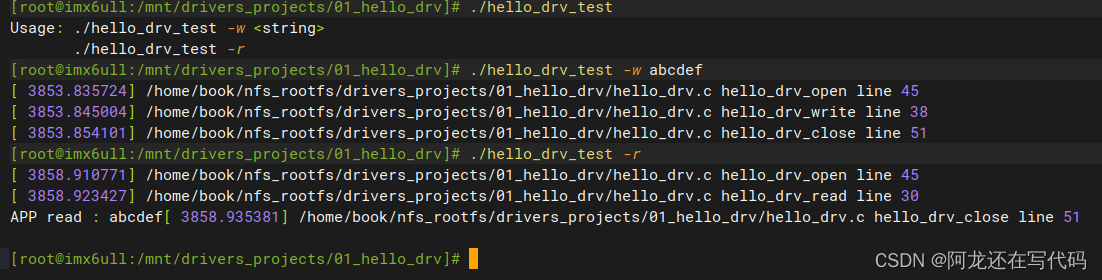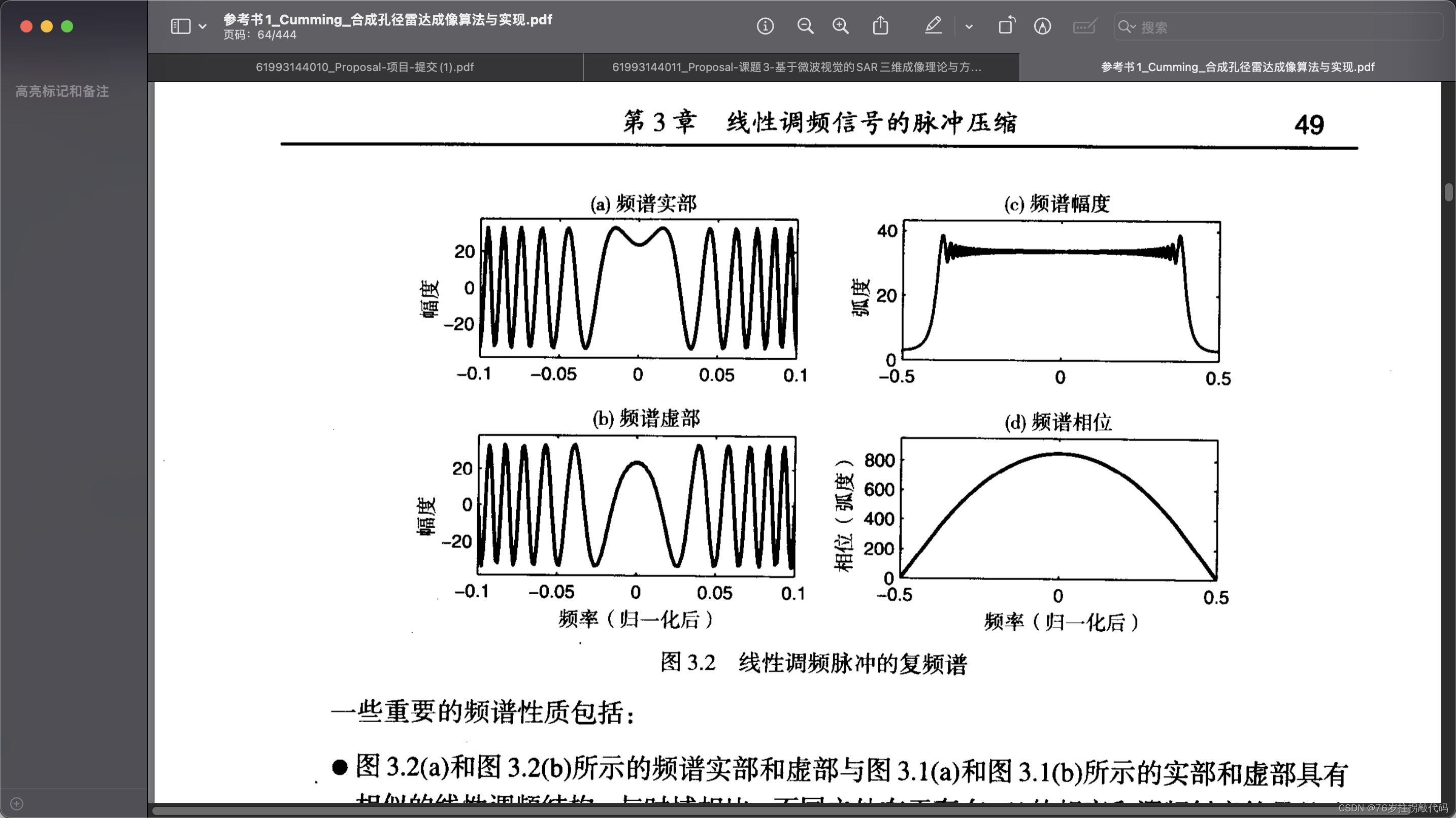
代码参数说明:Sf1为书中公式3.19,Sf2为时域信号快速傅里叶表达式,两种频谱表达式所做出的图可看出其区别
代码如下:
clc
clear all
close all
%参数设置
TBP = 720; %时间带宽积
T = 10e-6; %脉冲持续时间
%参数计算
B = TBP/T; %信号带宽
K = B/T; %线性调频频率
alpha = 1.25; %过采样率
F = alpha*B; %采样率
N = 2*ceil(F*T/2); %采样点数
dt = T/N; %采样时间间隔
df = F/N; %采样频率间隔
%变量设置
t = -T/2:dt:T/2-dt; %时间变量
f = -F/2:df:F/2-df; %频率变量
%信号表达
st = exp(1j*pi*K*t.^2); %chirp信号复数表达式
Sf1 = exp(-1j*pi*f.^2/K); %chirp信号频谱表达式
Sf2 = fftshift(fft(fftshift(st))); %chirp信号快速傅里叶变换
%绘图
%Sf1
figure
subplot(221),plot(f*1e-6,real(Sf1),'r')
axis([-10 10,-1.2 1.2])
subplot(222),plot(f*1e-6,abs(Sf1))
axis([-10 10,-1.2 1.2])
subplot(223),plot(f*1e-6,imag(Sf1),'r')
axis([-10 10,-1.2 1.2])
subplot(224),plot(f*1e-6,unwrap(angle(Sf1)))
axis([-28 28,0 400])
%Sf2
figure
subplot(221),plot(f*1e-6,real(Sf2),'r')
axis([-10 10,-40 40])
subplot(222),plot(f*1e-6,abs(Sf2))
axis([-50 50,-0 40])
subplot(223),plot(f*1e-6,imag(Sf2),'r')
axis([-10 10,-40 40])
subplot(224),plot(f*1e-6,unwrap(angle(Sf2)))
axis([-50 50,0 900])
1. N = 2*ceil(F*T/2);
ceil: 向正无穷舍入,保证N是偶数
2. plot(f*1e-6,unwrap(angle(Sf1)))
Q = unwrap(P) 展开向量 P 中的弧度相位角。每当连续相位角之间的跳跃大于或等于 π 弧度时,unwrap 就会通过增加 ±2π 的整数倍来平移相位角,直到跳跃小于 π。如果 P 是矩阵,unwrap 将按列运算。如果 P 是多维数组,unwrap 将对大小大于 1 的第一个维度进行运算。
举个例子:一般在我们计算一个系统相频特性时,就要用到反正切函数提取相位,计算机中反正切函数规定,在一、二象限中的角度为0~pi,三四象限的角度为0~-pi。但实际得到的结果会发生相位跳变,跳变幅度为2pi,这就叫相位的卷绕。unwrap函数的作用就是解卷绕,使相位在pi处不发生跳变,从而反应出真实的相位变化。