目录

题目：

示例：

分析：

代码：

---

题目：

示例：

分析：

题目给我们一个数组，让我们找出它的绝对值最大的子数组的和。

这边的子数组是要求连续的，让我们找出一个元素之和的绝对值最大的连续子数组。

要绝对值最大，那么就是两种情况，最大的正数以及最小的负数，所以我们可以兵分两路，一次寻找正数的最大值，一次寻找负数的最小值。

我们很容易就能想到使用滑动窗口，右窗口滑动用来吸收新的数，而左窗口滑动用来吐出不要的数。我们要使用滑动窗口就必须要搞清楚左窗口什么时候滑动，滑动到什么时候停止。

我们先看看怎么寻找正数的最大值，我们的右窗口一直往右扩张，直到如果窗口内的总和为负数了，那么目前为止的窗口总和就变成“累赘”了，因为我们要的是寻找最大的正数，一旦有负数了，我们就把窗口全部丢弃，从右窗口的右边再接着“滑动”。

那可能有人会问，为什么是把窗口全部丢弃，而不是开始滑动左窗口。

因为窗口的总和变为负数，这一结果是右窗口吸收新元素造成的，因此我们不需要的元素一定是靠近右窗口的，如果开始滑动左窗口，那么一开始滑出的只会是我们需要的正数，总和只会越来越小，直到左窗口和右窗口重叠，窗口总和变成0，然后再接着从右窗口的右边接着“滑动”。

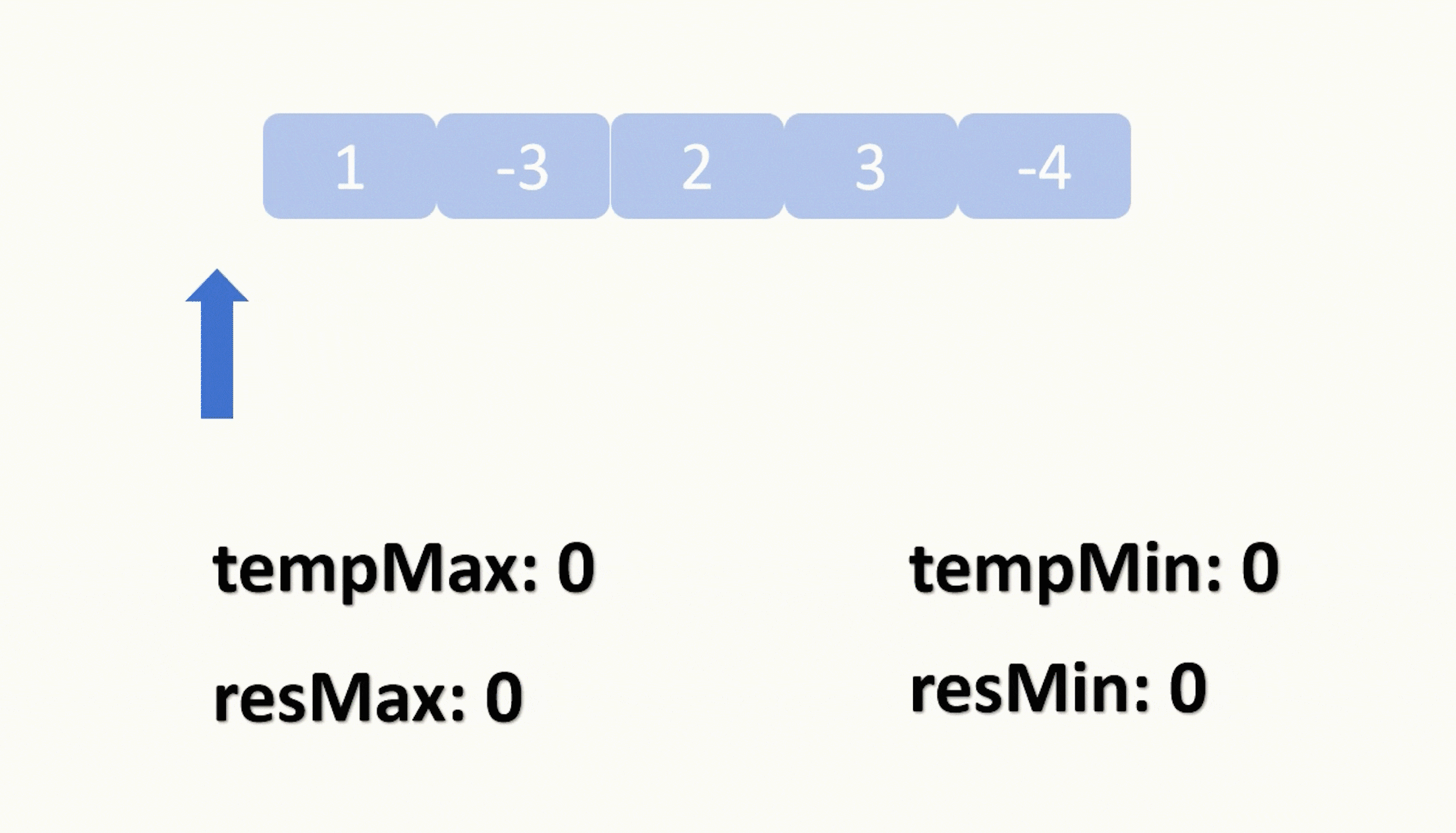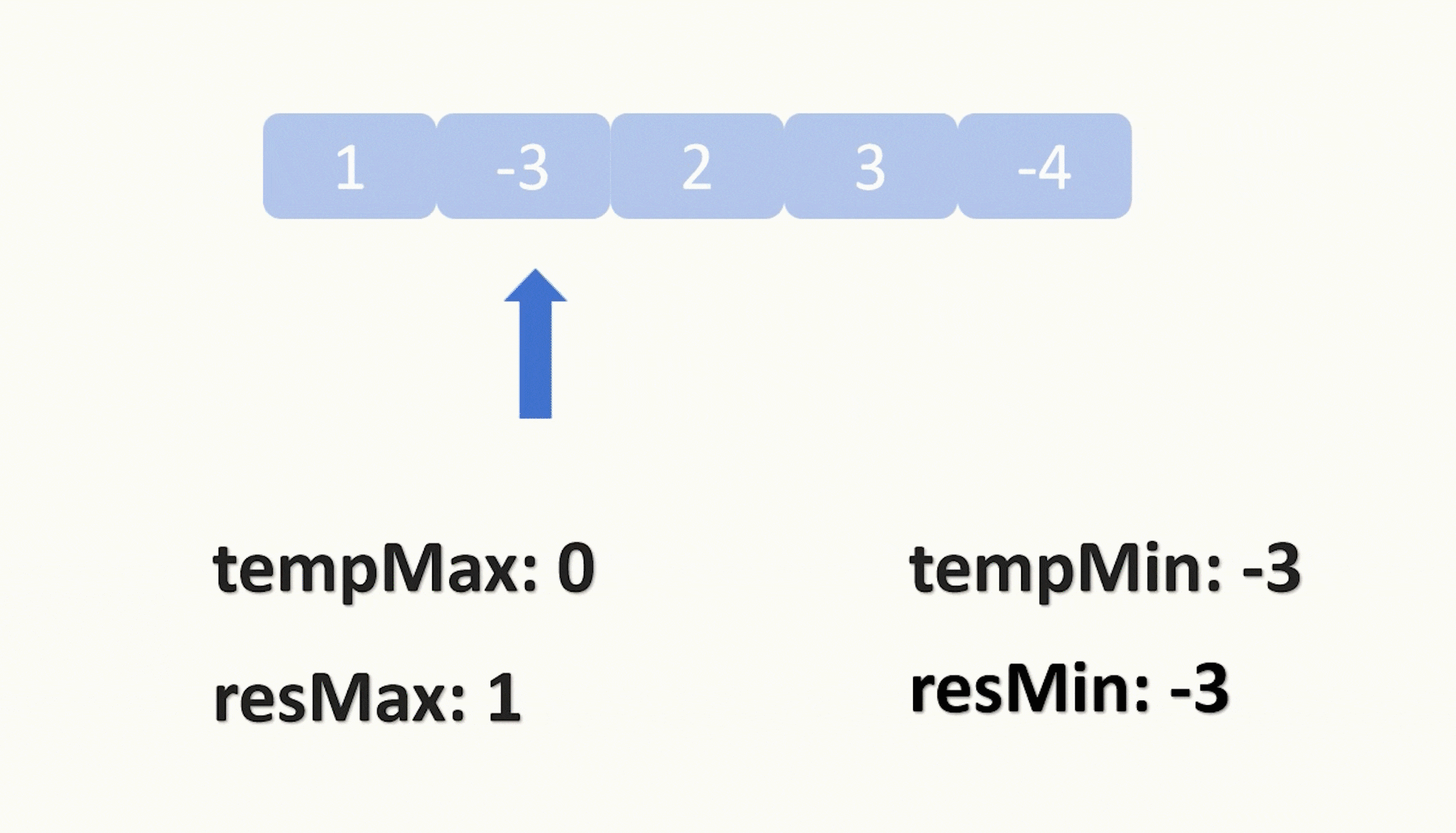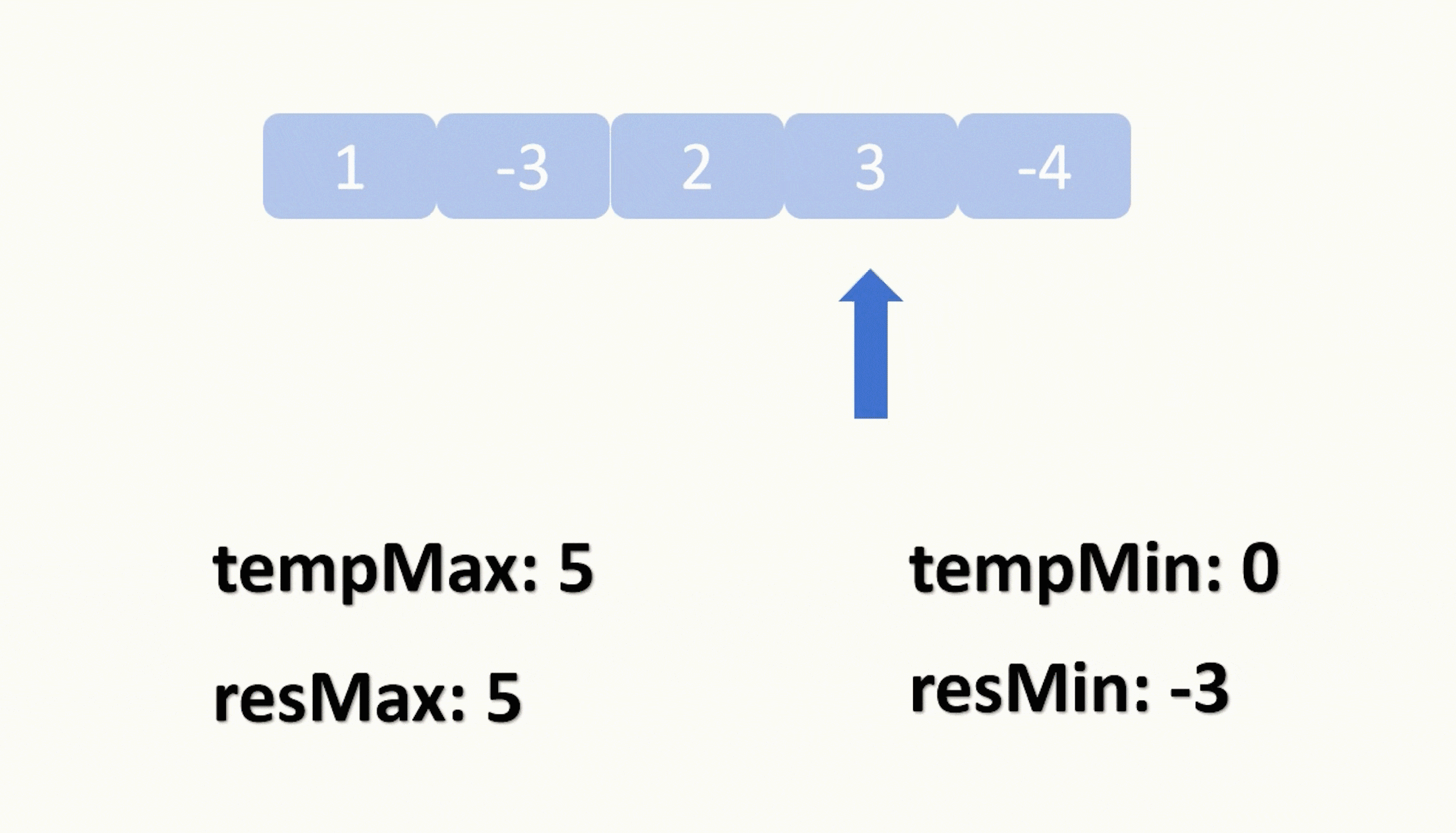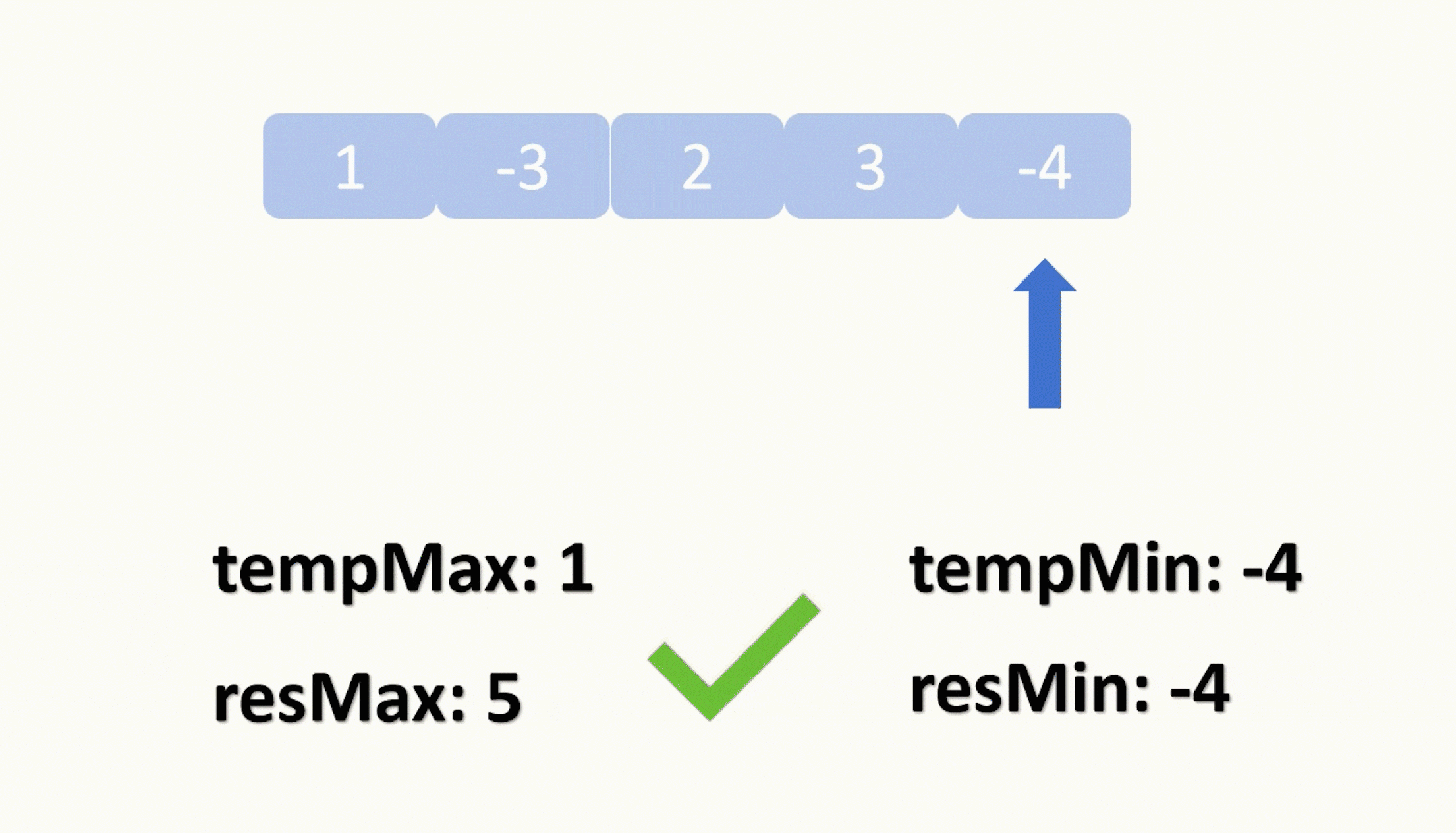
大家可能发现了，在本题中，我们的左窗口没有存在的必要，因为它不需要滑动，每次更新都是直接更新到右窗口的位置，所以我们只需要用一根指针来遍历原数组即可，此外还需要用两个变量，分别接收当前“窗口”内的正数最大值和我们已经获取到的正数的最大值。每次移动指针我们都判断当前“窗口”的总和有没有小于0，小于0就抛弃掉当前窗口，将窗口总和置为0，重新开始“滑动”。

那我们说完了怎么获取正数的最大值，还有一个就是要获取负数的最小值，这个也是上面的步骤，只不过是改变一下判断条件，就是判断当前窗口的总和有没有大于0，大于0就抛弃掉当前窗口，将窗口总和置为0，重新开始“滑动”。

上面两种可以同时进行，只是各自需要两个变量来分别记录和更新。

最后再比较一下，把正数的最大值和负的负数的最小值中最大的返回出去即可。

代码：

class Solution {
public:
    int maxAbsoluteSum(vector<int>& nums) {
        int maxRes=abs(nums[0]),minRes=abs(nums[0]);
        int tempMax=0,tempMin=0;
        for(int& num:nums){
            if(tempMax+num<=0) tempMax=0;
            else tempMax+=num;
            if(tempMin+num>=0) tempMin=0;
            else tempMin+=num;
            if(tempMin<minRes) minRes=tempMin;
            if(tempMax>maxRes) maxRes=tempMax;
        }
        return max(maxRes,-minRes);
    }
};