序号	内容
1	【数理知识】自由度 degree of freedom 及自由度的计算方法
2	【数理知识】刚体 rigid body 及刚体的运动
3	【数理知识】刚体基本运动，平动，转动
4	【数理知识】向量数乘，内积，外积，matlab代码实现
5	【数理知识】协方差，随机变量的的协方差，随机变量分别是单个数字和向量时的协方差
6	【数理知识】旋转矩阵的推导过程，基于向量的旋转来实现，同时解决欧式变换的非线性局限

1. 奇异值分解

讲解奇异值分解（Sigular Value Decomposition，SVD）的教程有很多，我这里不做赘述，仅记录下自己的理解。

针对以下奇异值分解公式：

$$\begin{array}{rl}M& =U\Sigma V^{\text{T}}\end{array}$$

其中：
$M$ 矩阵可以不是方阵，也就是其维度为 $m\times n$。
$U$ 矩阵是 $m\times m$ 的方阵，表示分解后的基向量。
$\Sigma$ 矩阵是非方阵维度为 $m\times n$ 的对角矩阵，对角元素是奇异值。
$V$ 矩阵是维度为 $n\times n$ 的正交矩阵。

---

比如说，当 $M$ 的矩阵维度为 $4\times 2$ 时，奇异值分解公式就可以写成如下形式

$$\begin{array}{rl}M& =U\Sigma V^{\text{T}}\\ \left[\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\\ x_3& y_3\\ x_4& y_4\end{array}\right]& =\left[\begin{array}{cccc}—& —& —& —\\ —& —& —& —\\ —& —& —& —\\ —& —& —& —\end{array}\right]\left[\begin{array}{cc}a& 0\\ 0& b\\ 0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{cc}—& —\\ —& —\end{array}\right]\end{array}$$

到这里可能不太明白，没关系，之前只是为了先把 SVD 公式回顾一下，往下继续看就行了。

---

2. 由数据的线性变换出发

数据的线性变换（Linear Transformation）是一个数学上的概念，通常用于更改数据的表示或基准，但不改变数据的本质结构或关系。而在向量空间中，线性变换可以通过乘以一个矩阵来实现。

假如存在一个二维平面的向量，线性变换可以是缩放、旋转、倾斜等操作。

例如，

• 一个缩放操作可以使用矩阵 $S=\left[\begin{array}{cc}2& 0\\ 0& 1\end{array}\right]$ 表示，此矩阵会将 $x$ 坐标乘以 2，$y$ 坐标乘以 1。

• 一个旋转操作可以使用矩阵 $R=\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$ 表示，此矩阵会将 $x$ 和 $y$ 旋转 $\theta$ 角度。

---

上述两个矩阵 $S$ 和 $R$ 也可以从正交基 $\vec{i},\vec{j}$ 的变换上分别看到 $S$ 和 $R$ 矩阵的变换效果。

如果原本正交基为 $\vec{i}=\left[\begin{array}{c}1\\ 0\end{array}\right]，\vec{j}=\left[\begin{array}{c}0\\ 1\end{array}\right]$，经过 $S$ 矩阵的变换后，
变换后正交基变为 $S\vec{i}=\left[\begin{array}{c}2\\ 0\end{array}\right]，S\vec{j}=\left[\begin{array}{c}0\\ 1\end{array}\right]$。

如果原本正交基为 $\vec{i}=\left[\begin{array}{c}1\\ 0\end{array}\right]，\vec{j}=\left[\begin{array}{c}0\\ 1\end{array}\right]$，经过 $R$ 矩阵的变换后，
变换后正交基变为 $R\vec{i}=\left[\begin{array}{c}\cos (\theta )\\ \sin (\theta )\end{array}\right]，R\vec{j}=\left[\begin{array}{c}-\sin (\theta )\\ \cos (\theta )\end{array}\right]$。

---

在视频【学长小课堂】什么是奇异值分解SVD–SVD如何分解时空矩阵 - bilibili中，举例用的是一组向量

$$D=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ y_1& y_2& y_3& y_4\end{array}\right]$$

也可以理解为一群二维平面的数据点。

接下来再看一下这一群数据点的拉伸和旋转操作，因为视频中有相应的动画，更便于理解。

---

1. 缩放

针对上述 $D$ 数据点矩阵，看一下变换矩阵 $S$ 的效果。

从形式上可以看到矩阵 $S$ 的作用是缩放，这一点也可以从以下数据运算上看出，即当 $D$ 左乘一个变换矩阵 $S$ 后，$D$ 变为

$$\begin{array}{r}SD=\left[\begin{array}{cc}2& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ y_1& y_2& y_3& y_4\end{array}\right]=\left[\begin{array}{cccc}2x_1& 2x_2& 2x_3& 2x_4\\ y_1& y_2& y_3& y_4\end{array}\right]\end{array}$$

---

上述变换也可以从以下动态图上看到数据的变换效果。

---

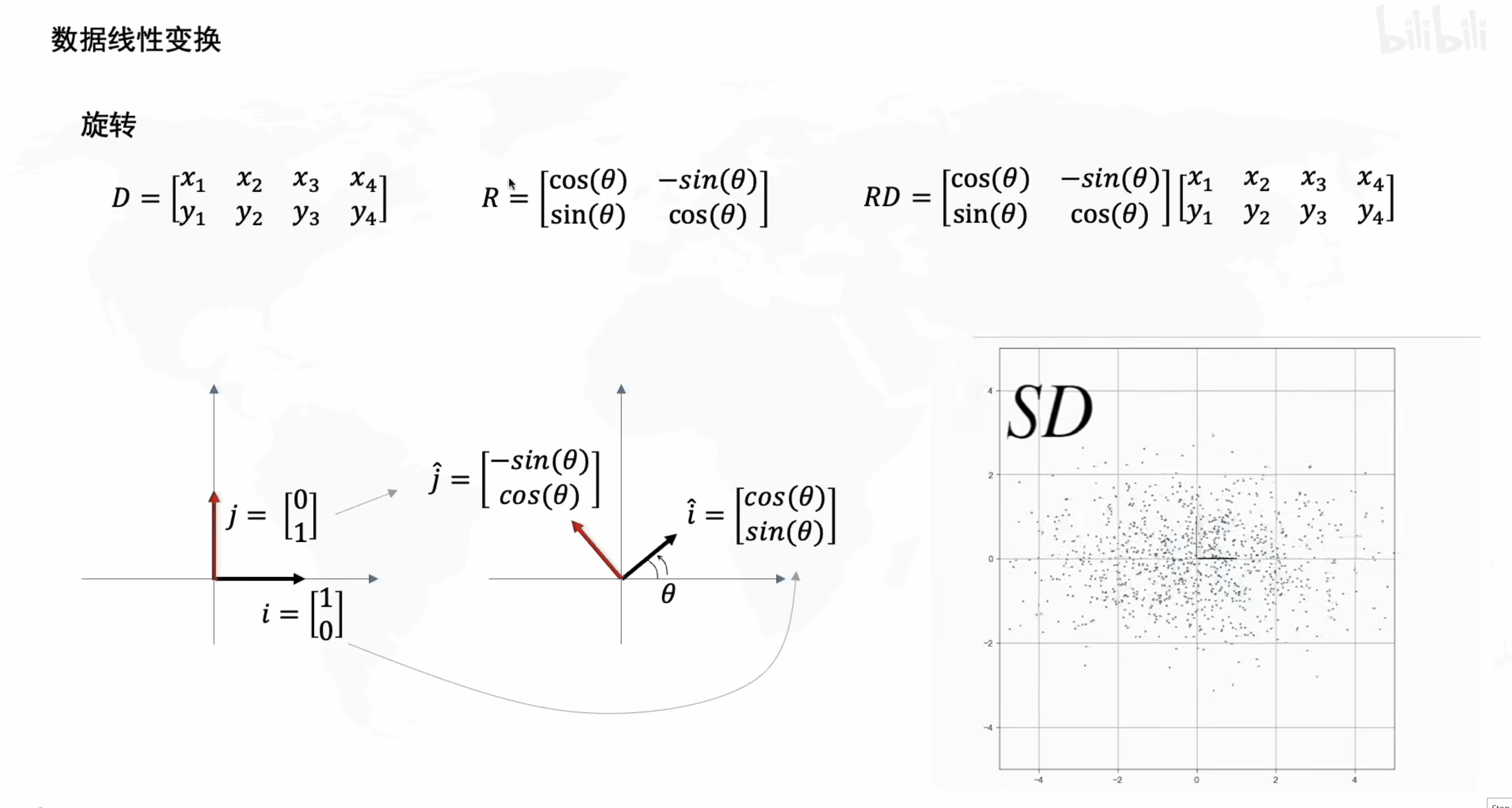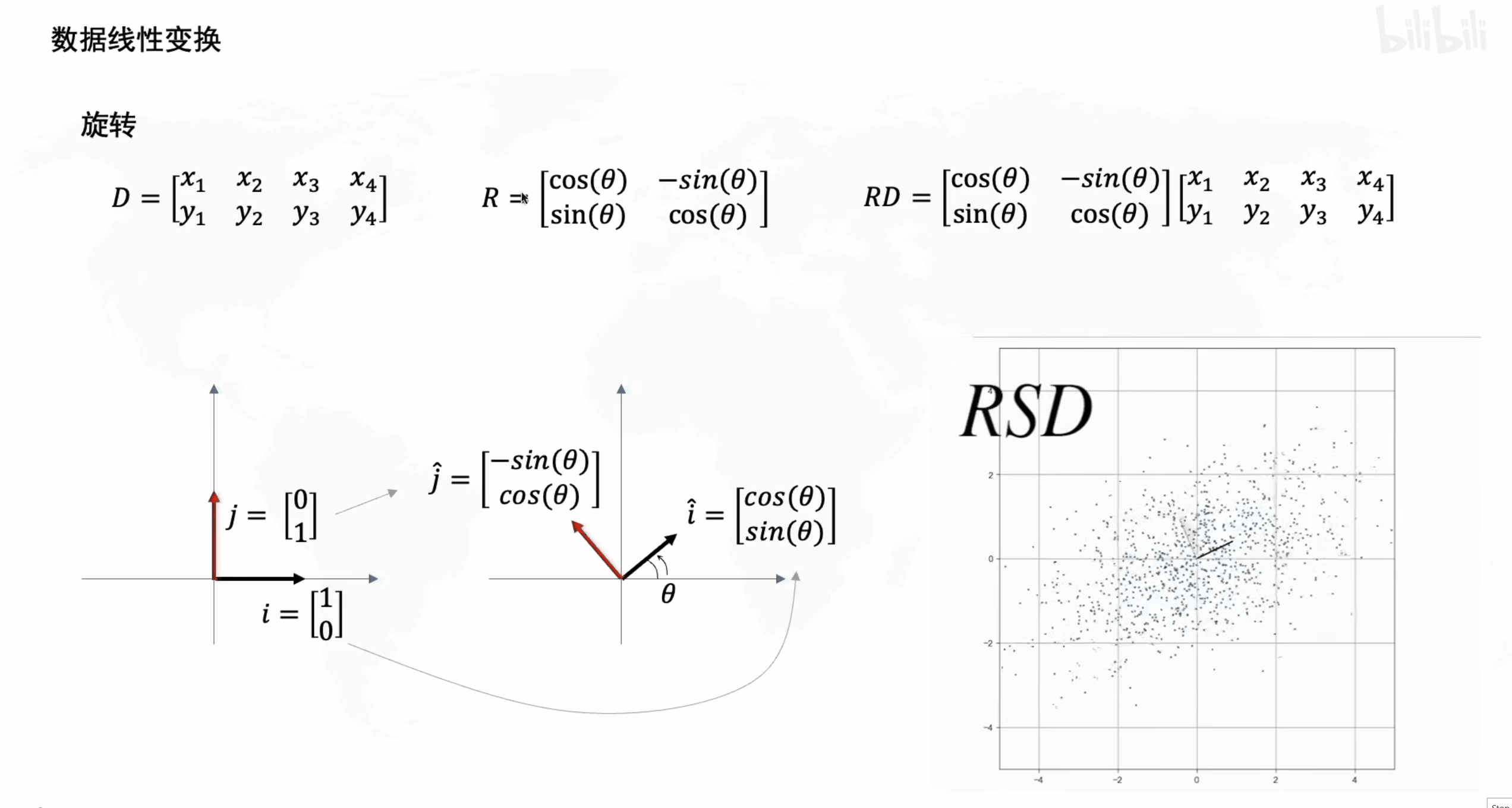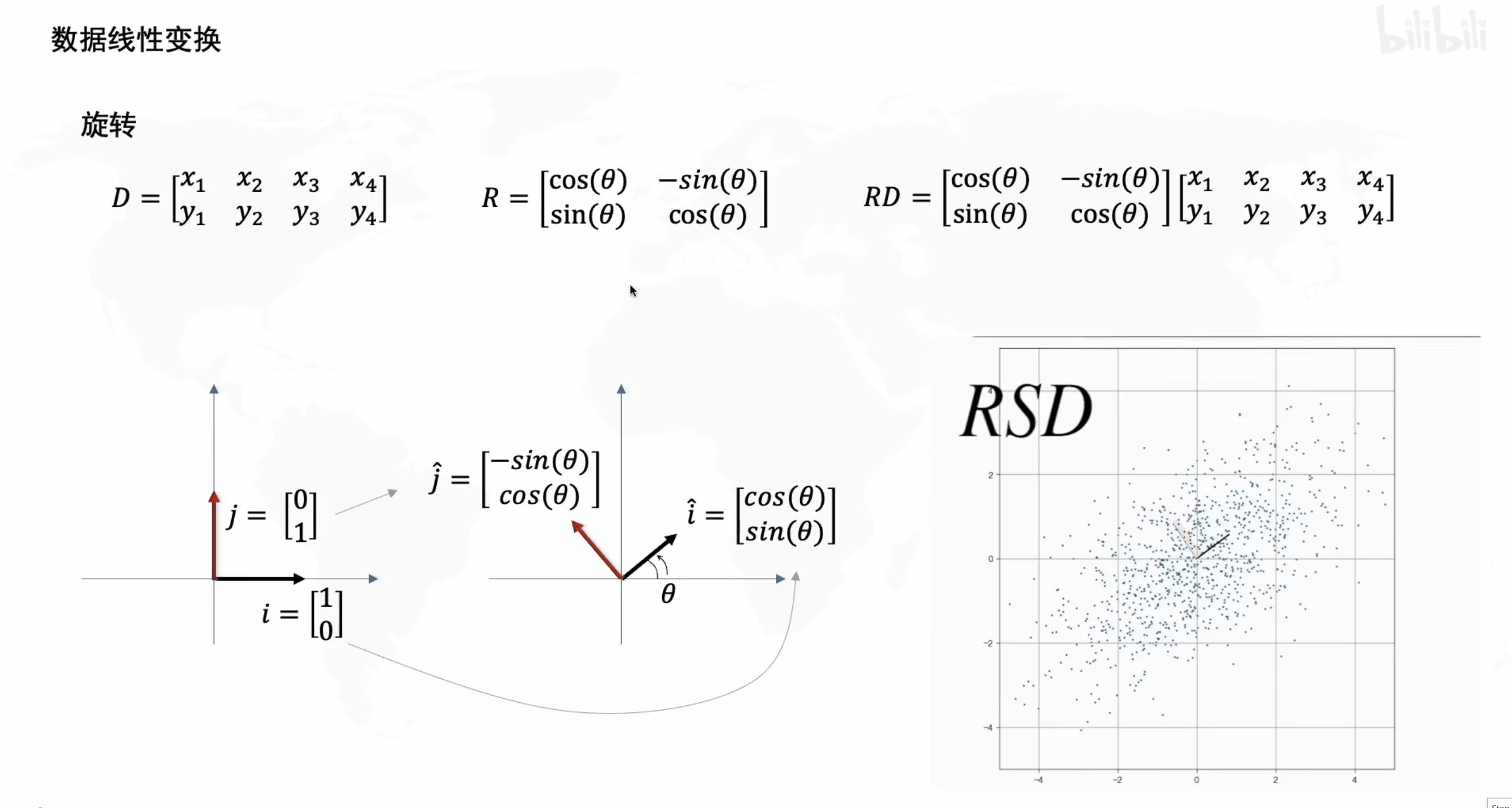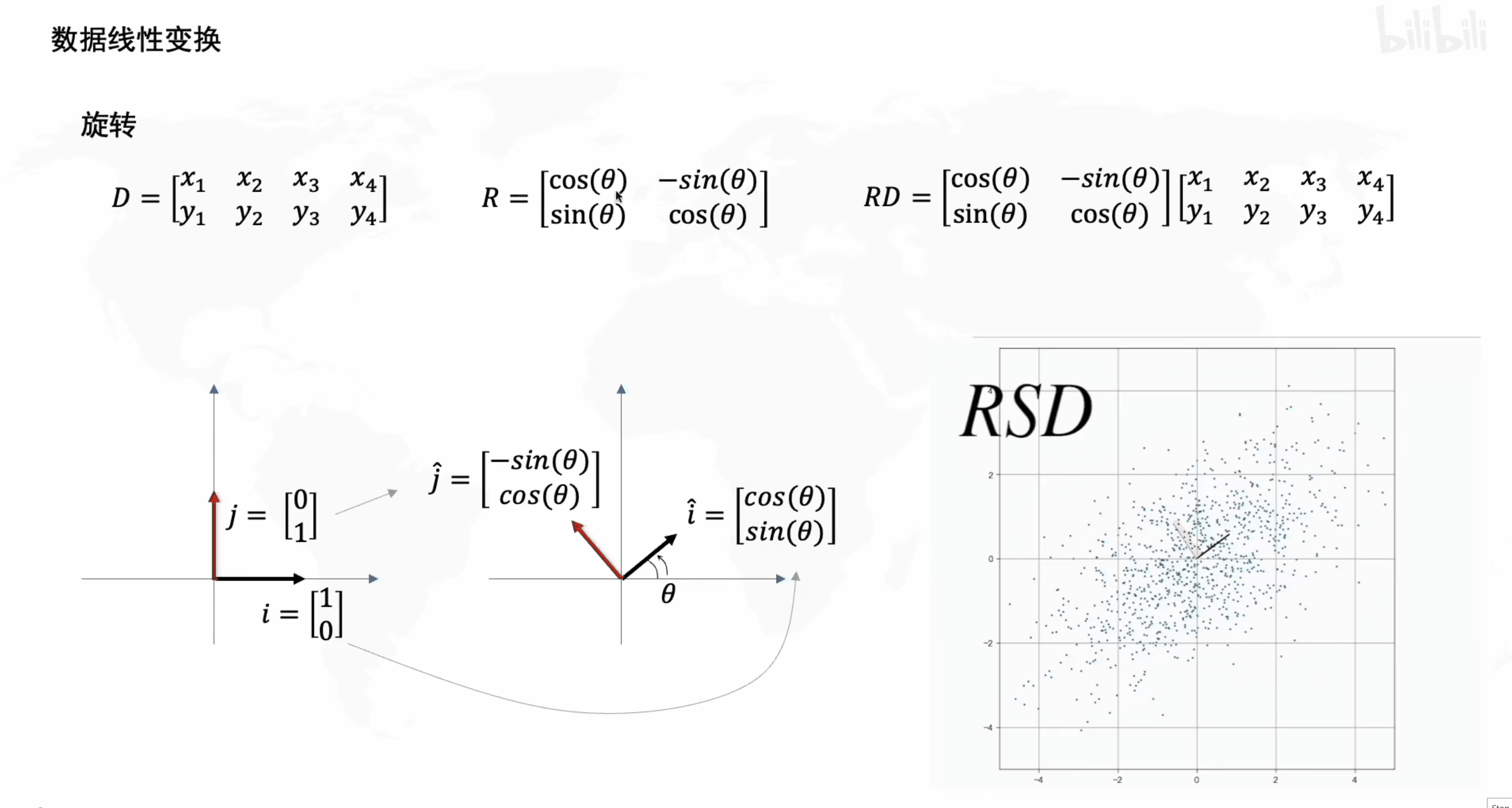
2. 旋转

接下来看一下旋转矩阵 $R$ 的效果。

从形式上可以看到矩阵 $R$ 的作用是旋转，这一点也可以从以下数据运算上看出，即当经过拉伸的 $SD$ 矩阵再左乘一个变换矩阵 $R$ 后，$SD$ 变为

$$\begin{array}{r}RSD=\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ y_1& y_2& y_3& y_4\end{array}\right]=\left[\begin{array}{ccc}{x}_1\cos (\theta )-y_1\sin (\theta )& x_2\cos (\theta )-y_2\sin (\theta )& \cdots \\ x_1\sin (\theta )+y_1\cos (\theta )& x_2\sin (\theta )+y_2\cos (\theta )& \cdots \end{array}\right]\end{array}$$

---

数据 $SD$ 的旋转效果可观察如下动态图。

---

3. 补充知识：如何分辨矩阵的变换效果

要分析一个矩阵的变换效果（是否是缩放、旋转或倾斜），我们需要考虑矩阵如何操作基向量或观察它的特定属性。

1. 缩放:
   缩放矩阵会在对角线上有非 1 的值，其它位置为 0。例如，二维空间中的缩放矩阵为：
   $$\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]$$
   其中 $s_x,s_y$ 分别是 $x$ 方向和 $y$ 方向的缩放因子。

2. 旋转：
   旋转矩阵在二维空间中具有以下形式：
   $$\left[\begin{array}{cc}\cos (\theta )& -\sin (\theta )\\ \sin (\theta )& \cos (\theta )\end{array}\right]$$
   其中 $\theta$ 是旋转的角度。旋转矩阵的行列式为 1，且其逆矩阵是它的转置。
   另外，三维空间旋转矩阵的基向量形式请参考【数理知识】旋转矩阵的推导过程，基于向量的旋转来实现，同时解决欧式变换的非线性局限，欧拉角形式请参考：第3章-数理知识基础 -＞ 坐标转换。

3. 倾斜或剪切：
   在二维空间中，$x$ 和 $y$ 方向的倾斜矩阵为：
   $$\left[\begin{array}{cc}1& s\\ 0& 1\end{array}\right],\left[\begin{array}{cc}1& 0\\ s& 1\end{array}\right]$$
   其中 $s$ 是剪切或倾斜的量。

---

在实际的应用中，一个矩阵可能同时表示了多种变换，也就是一个矩阵是多种变化的组合。为了确定其作用，我们通常需要对其进行分解，例如常见的 SVD 分解可以得到旋转、缩放和剪切矩阵。

同时，如果想直观地了解矩阵是如何操作的，也可以将其应用在标准基向量（如二维空间中的 $\left[\begin{array}{c}1\\ 0\end{array}\right]$ 和 $\left[\begin{array}{c}0\\ 1\end{array}\right]$）上，观察向量基的变换结果。

---

3. 从 $2\times 2$ 矩阵中得到 SVD 公式

有了上述基础知识，现在我们假设存在一个 $2\times 2$ 的矩阵 $M$。可以知道 $M$ 矩阵一定是表示了某种线性变换，至于是一种还是多种的组合，我们需要进一步分析。

---

假设 $M$ 矩阵的变换效果如下图所示

我们可以在变换前的坐标轴上找到一组标准正交基，称为 ${\vec{v}}_1,{\vec{v}}_2$，经过 $M$ 线性变换后，${\vec{v}}_1$ 变为 ${\vec{u}}_1$，${\vec{v}}_2$ 变为 ${\vec{u}}_2$，同时长度分别为 ${\sigma }_1$ 和 ${\sigma }_2$。此过程可以用如下关系式表示

$$\begin{array}{rl}M{\vec{v}}_1& ={\sigma }_1{\vec{u}}_1\\ M{\vec{v}}_2& ={\sigma }_2{\vec{u}}_2\end{array}$$

---

解析来用矩阵来表示正交基，也就是

$$\begin{array}{rl}V=\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right],U& =\left[\begin{array}{cc}{\vec{u}}_1& {\vec{u}}_2\end{array}\right],\Sigma =\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& {\sigma }_2\end{array}\right]\end{array}$$

那么有

$$\begin{array}{rl}M\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right]& =\left[\begin{array}{cc}{\vec{u}}_1& {\vec{u}}_2\end{array}\right]\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& {\sigma }_2\end{array}\right]\\ MV& =U\Sigma \\ MV{V}^{-1}& =U\Sigma V^{-1}\\ M& =U\Sigma V^{\text{T}}（V是\text{正交矩阵，故}{V}^{-1}=V^{\text{T}}）\end{array}$$

---

从图形变换上来看 SVD 分解，矩阵 $M$ 等价于先经过旋转矩阵 $V^{\text{T}}$ 进行旋转，再经过缩放矩阵 $\Sigma$ 进行缩放，最后通过旋转矩阵 $U$ 进行旋转，就达到了和 $M$ 矩阵一样的线性变换效果。

---

4. SVD 推广到 $m\times n$ 矩阵

上述奇异值分解例子中

$$\begin{array}{rl}M& =U\Sigma V^{\text{T}}\end{array}$$

矩阵的维度分别为：
$M$：$2\times 2$，
$U$：$2\times 2$，
$\Sigma$：$2\times 2$，
$V$：$2\times 2$。

若 $M$ 的矩阵维度为 $m\times n$，那么有
$U$：$m\times m$，
$\Sigma$：$m\times n$，
$V$：$n\times n$。

到这里也就与我们第一步所讲述的对应上了。

---

5. 求 SVD 分解

我们知道 SVD 分解的基本形式为

$$\begin{array}{rl}M& =U\Sigma V^{\text{T}}\end{array}$$

那么
$$\begin{array}{rl}{M}^{\text{T}}M& =(U\Sigma V^{\text{T}}{)}^{\text{T}}U\Sigma V^{\text{T}}\\ M^{\text{T}}M& =V{\Sigma }^{\text{T}}{U}^{\text{T}}U\Sigma V^{\text{T}}\end{array}$$

因为 $U$ 是正交矩阵，所以有 $U^{\text{T}}U=I$，那么

$$\begin{array}{rl}{M}^{\text{T}}M& =V{\Sigma }^{\text{T}}{U}^{\text{T}}U\Sigma V^{\text{T}}\\ M^{\text{T}}M& =V{\Sigma }^{\text{T}}I\Sigma V^{\text{T}}\\ M^{\text{T}}M& =V{\Sigma }^{\text{T}}\Sigma V^{\text{T}}\end{array}$$

又因为 $\Sigma$ 是对角矩阵，所以有 ${\Sigma }^{\text{T}}=\Sigma$，即

$$\begin{array}{rl}{M}^{\text{T}}M& =V{\Sigma }^{\text{T}}\Sigma V^{\text{T}}\\ M^{\text{T}}M& =V\Sigma \Sigma V^{\text{T}}\end{array}$$

令 $L=\Sigma \Sigma$，有

$$\begin{array}{rl}{M}^{\text{T}}M& =V\Sigma \Sigma V^{\text{T}}\\ M^{\text{T}}M& =VL{V}^{\text{T}}\end{array}$$

因为 $V$ 也是正交矩阵，故可以进行如下移项

$$\begin{array}{rl}{M}^{\text{T}}M& =VL{V}^{\text{T}}\\ M^{\text{T}}MV& =VL{V}^{\text{T}}V=VL{V}^{-1}V\\ M^{\text{T}}MV& =VL\end{array}$$

---

这里需要使用特征向量的定义，忘记的可以参考文章【数理知识】特征值、特征向量、左特征向量。

当我们想去求取 $M^{\text{T}}M$ 的特征向量时，根据定义式有

$$\begin{array}{rl}{M}^{\text{T}}M{\vec{v}}_1& ={\lambda }_1{\vec{v}}_1\\ M^{\text{T}}M{\vec{v}}_2& ={\lambda }_2{\vec{v}}_2\end{array}$$

换种形式写一下有

$$\begin{array}{rl}{M}^{\text{T}}M\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right]& =\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right]\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]\end{array}$$

---

再看一下之前得到的结论

$$\begin{array}{rl}{M}^{\text{T}}MV& =VL\end{array}$$

所以 $V$ 是 $M^{\text{T}}M$ 矩阵的特征向量，$L$ 是其特征值。

而 $L=\Sigma \Sigma$ 矩阵是对角线矩阵 $\Sigma$ 的乘，即

$$\begin{array}{rl}L& =\Sigma \Sigma =\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& {\sigma }_2\end{array}\right]\left[\begin{array}{cc}{\sigma }_1& 0\\ 0& {\sigma }_2\end{array}\right]=\left[\begin{array}{cc}{\sigma }_1^2& 0\\ 0& {\sigma }_2^2\end{array}\right]\\ & =\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]\end{array}$$

同时 $\Sigma$ 矩阵中的元素 ${\sigma }_1$ 我们称之为奇异值。

通过上式我们也知道为什么奇异值和特征值之间是一个平方的关系了。

---

同理，我们可以得到

$$\begin{array}{rl}M{M}^{\text{T}}U& =UL\end{array}$$

往下也是同样的结论，即 $U$ 是 $M{M}^{\text{T}}$ 矩阵的特征向量。

---

总结下来，求解 SVD 的过程为

1. 求 $M^{\text{T}}M$ 的特征向量得到 $V$，
2. 求 $M{M}^{\text{T}}$ 的特征向量得到 $U$，
3. 求 $M^{\text{T}}M$ 或 $M{M}^{\text{T}}$ 的特征值，开方得到奇异值，
4. 用奇异值构成对角阵 $\Sigma$。

---

Ref

1. 如何通俗易懂地讲解什么是 PCA（主成分分析）？ - 知乎
2. 【机器学习】降维——PCA（非常详细） - 知乎
3. 【学长小课堂】什么是奇异值分解SVD–SVD如何分解时空矩阵 - bilibili
4. 如何通俗地理解奇异值？ - 马同学

---