TopK
在N个数中 找出最大或最小的前k个数,就是TopK算法。比如有一组数字,[1,2,3,4,5,6,7,8,9],这组数中最大的前 3(k)个数是 9,8,7。最小的 前3个数是 1,2,3。而TopK算法就是找出最大或者最小的前K个数。我们就用堆来实现。
之前讲解过如何写一个堆,博客链接 ,代码git链接。
今天我们就用这个堆,来实现TopK算法。
算法思路
我们可以构建一个 有K个数的小堆,依次Push。
比如上面举的例子,1-9,找出最大的前3个数。
那么此时,K = 3, 找最大的前3个数,我们就构建小堆。
我们随机取3个数,2,6,9,放入小堆中。
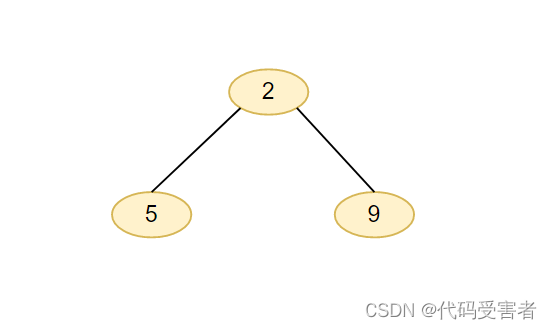
随后我们拿剩下 N - K个数与堆顶进行比较,如果比堆顶大,那么就用这个数替换堆顶,随后进行向下调整。
第一次比较

第二次比较

第三次比较

上面三次都没有发生向下调整,因为堆顶的元素比它的两个孩子小,但下一次比较会发生向下调整!
第四次比较

向下调整后,我们就发现,堆顶元素变成了 5。
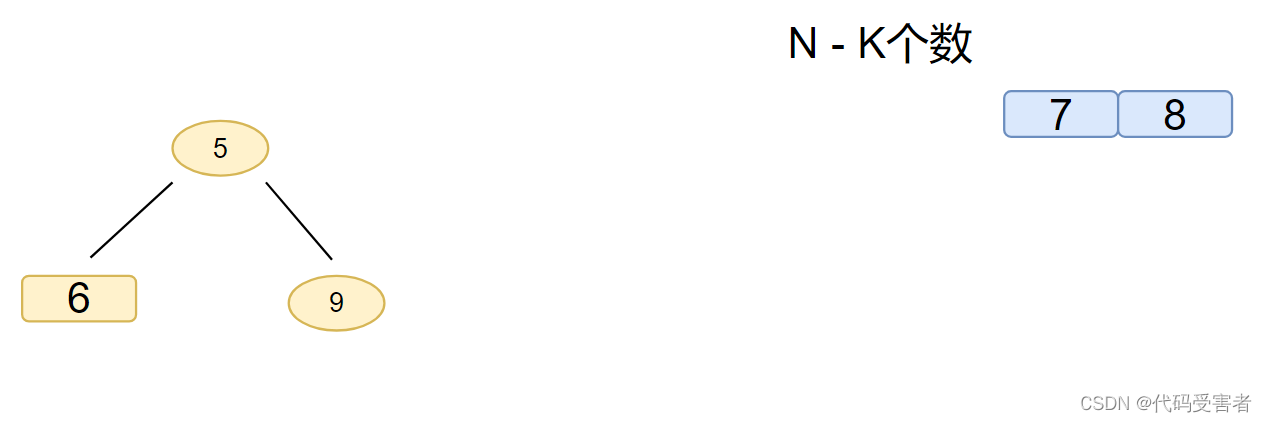
第五次比较和第四次比较一样,会发生向下调整。
第五次比较

第6次比较

比较完之后,我们会发现我们的堆是这样的
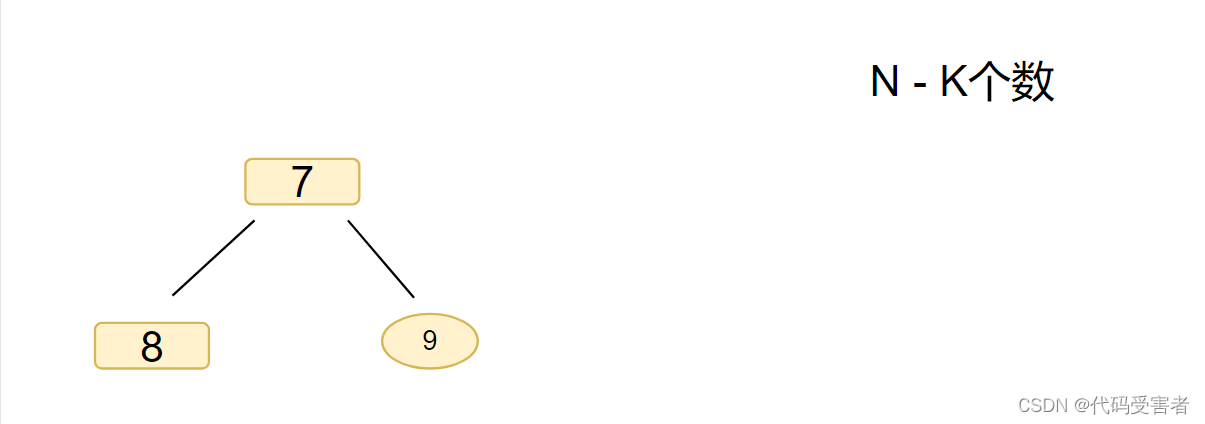
我们可以发现,7,8,9 就是我们 1 - 9 中 最大的前3个数。
代码实现
那么代码我们就可以这样写。
void PrintTopK(int* data, int len, int k)
{
//建立一个堆
HP hp;
HeapInit(&hp);
//插入K个数据
for (int i = 0; i < k; i++)
{
HeapPush(&hp, data[i]);
}
//随后进行比较,是否比栈顶元素大
for (int i = k; i < len; i++)
{
if (data[i] > HeapTop(&hp))
{
//交换位置
//把堆顶元素删掉
HeapPop(&hp);
//Push新数据
HeapPush(&hp, data[i]);
}
}
HeapPrint(&hp);
}
void TopKTest()
{
int n = 50000;
//开辟1万个数组 的空间
int* a = (int*)malloc(sizeof(int) * n);
for (int i = 0; i < n; i++)
{
a[i] = rand() % 1000000;
}
int k = 10;
//给上10个最大值
a[20009] = 1000000 + 1;
a[30007] = 1000000 + 2;
a[20006] = 1000000 + 3;
a[10008] = 1000000 + 4;
a[10007] = 1000000 + 5;
a[16000] = 1000000 + 6;
a[10005] = 1000000 + 7;
a[40004] = 1000000 + 8;
a[30003] = 1000000 + 9;
a[10001] = 1000000 + 10;
PrintTopK(a,n,k);
}
int main()
{
srand(time(NULL));
TopKTest();
return 0;
}
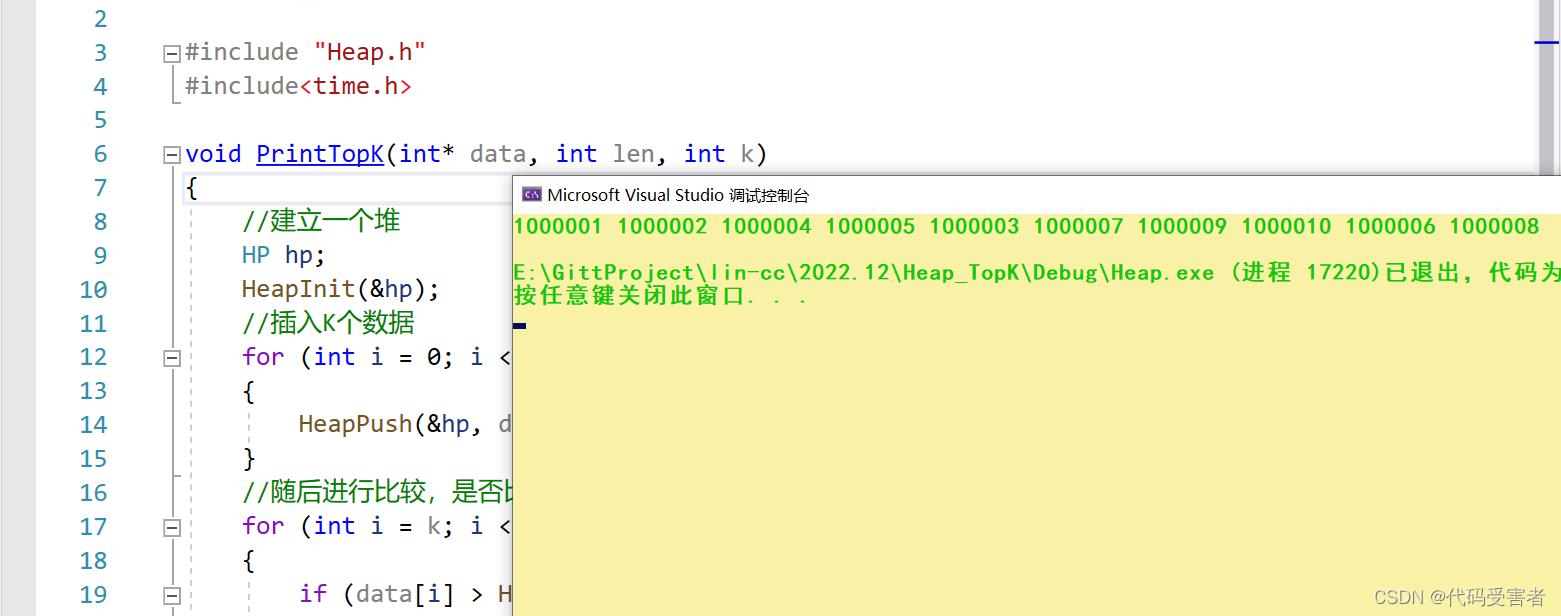
如果要找10个最小值的话,我们只需要把向上调整和向下调整的条件改一下。
TopK代码
void PrintTopK(int* data, int len, int k)
{
//建立一个堆
HP hp;
HeapInit(&hp);
//插入K个数据
for (int i = 0; i < k; i++)
{
HeapPush(&hp, data[i]);
}
//随后进行比较,是否比栈顶元素大
for (int i = k; i < len; i++)
{
//大堆,大端找最小值,小端找最大值
if (data[i] < HeapTop(&hp))
//小堆
//if (data[i] > HeapTop(&hp))
{
//交换位置
//把堆顶元素删掉
HeapPop(&hp);
//Push新数据
HeapPush(&hp, data[i]);
}
}
HeapPrint(&hp);
}
向上调整代码
void AdjustUp(HeapDataType* data, int child)
{
//至少比较一次
do
{
int parent = (child - 1) / 2;
//大堆
if (data[parent] < data[child])
//小堆
//if (data[parent] > data[child])
{
//交换
Swap(&data[parent],&data[child]);
//更新child
child = parent;
}
else
{
break;
}
} while (child > 0);
}
向下调整代码
//向下调整
void AdjustDown(HeapDataType* data, int n , int parent)
{
//定义左孩子节点
int child = parent * 2 + 1;
while (child < n)
{
//大堆
if (child+1 < n && data[child + 1] > data[child])
//小堆
//if (child + 1 < n && data[child + 1] < data[child])
{
child++;
}
//然后和父亲元比较
//大堆
if (data[child] > data[parent])
//小堆
//if ( data[child] < data[parent] )
{
//位置交换
Swap(&data[parent], &data[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
只要把标注了大端小端的if判断改一下,即可切换
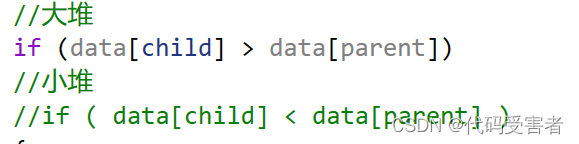
找10个最小值的运行结果

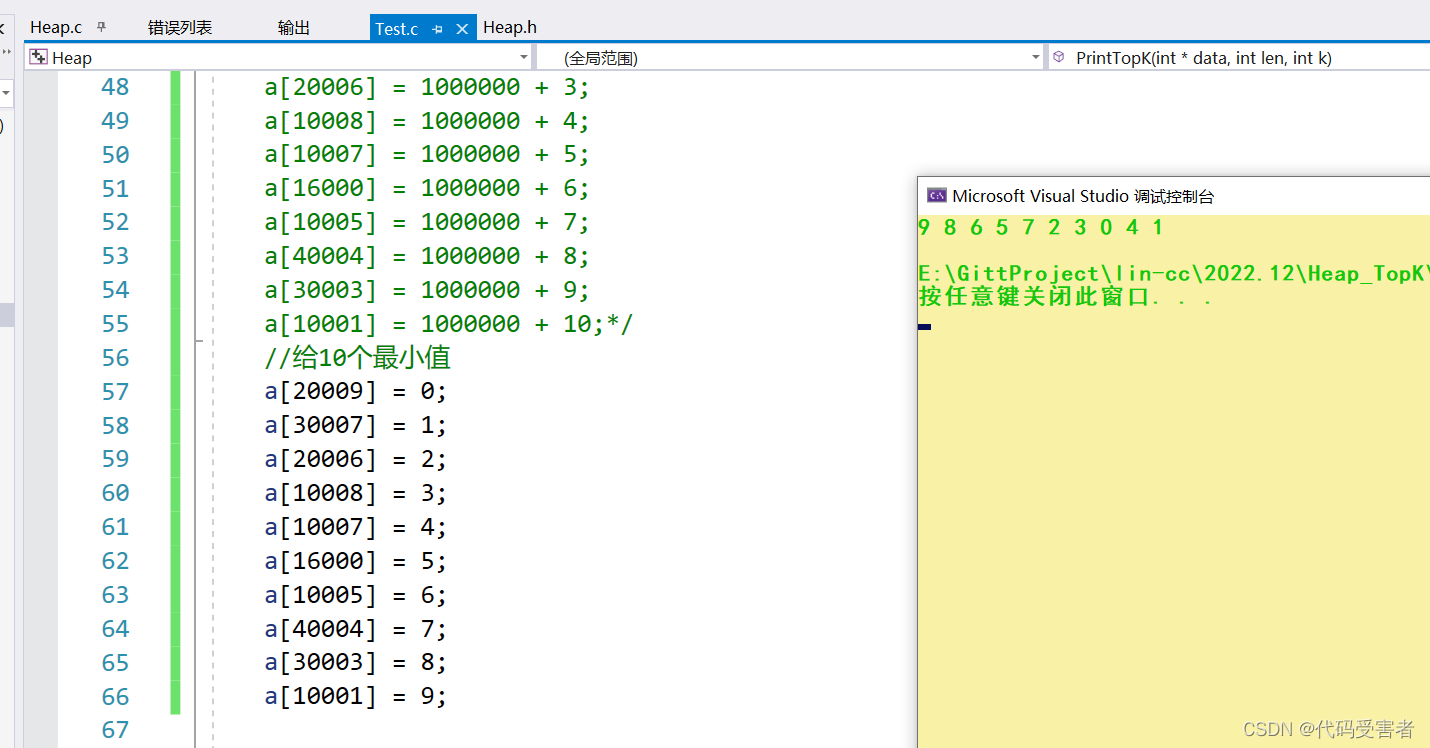
用堆实现TopK算法就到这里了,代码的Git链接







![[附源码]计算机毕业设计基于Java酒店管理系统Springboot程序](https://img-blog.csdnimg.cn/8b77efbf25c64a7fac9bd35a9e476171.png)