题目

二维平面，左下角(0,0)右上角(n,m)(1<=n,m<=1e6)的一块矩形，

q(q<=2e3)次线段切割操作，操作分四种：

ai 1 x，表示切割(x,m)到(x,m-ai)这条竖直线段(0<=x<=n,1<=ai<=1e6)

ai 2 x，表示切割(x,0)到(x,ai)这条竖直线段(0<=x<=n,1<=ai<=1e6)

ai 3 x，表示切割(0,x)到(ai,x)这条竖直线段(0<=x<=m,1<=ai<=1e6)

ai 4 x，表示切割(n-ai,x)到(n,x)这条竖直线段(0<=x<=m,1<=ai<=1e6)

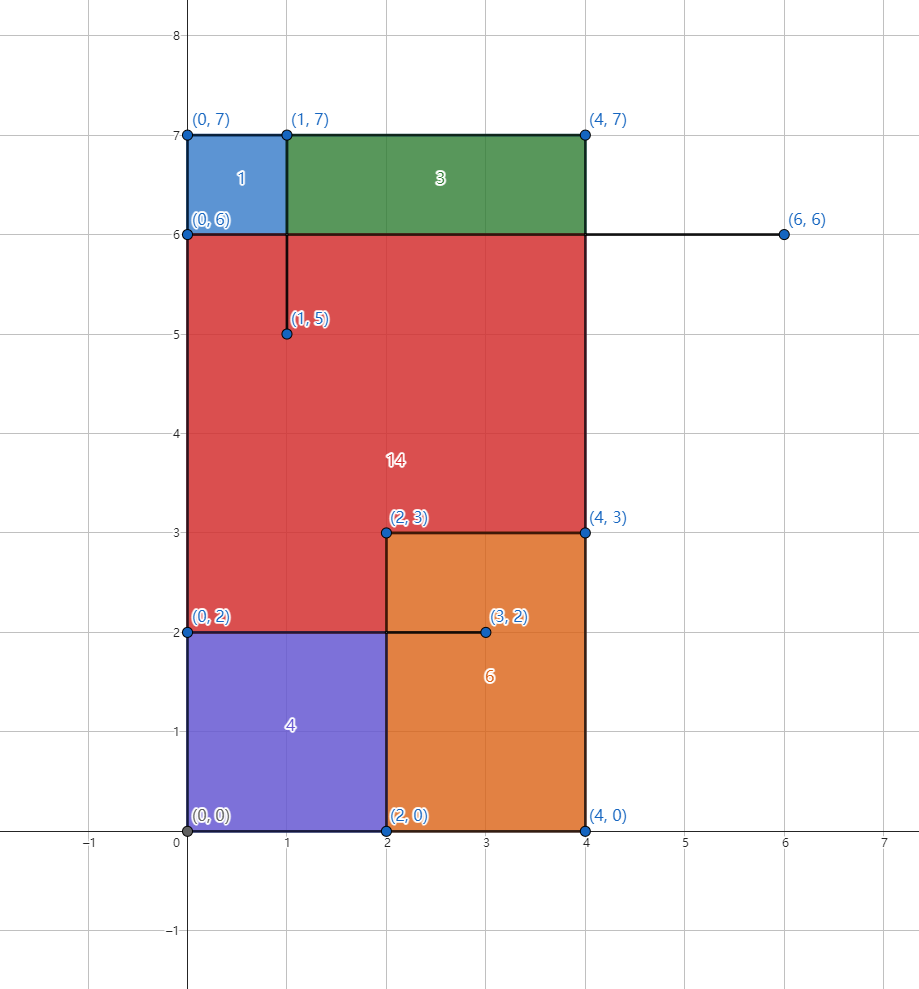
求切割后的最大矩形面积，如图所示，样例最大面积为14

 

思路来源

aging佬代码

题解

离散化，维护up dow lef rig表示四个方向线段的最小、最大、最大、最小的值

上下两个连通块能联通当且仅当左侧的线和右侧的线没有切断这两个连通块

即左侧的线在右侧的点左边，右侧的线在左侧的点右边，左侧的线小于右侧的线

代码1

#include<bits/stdc++.h>
using namespace std;
const int N=2e3+10,M=1e6+10;
typedef long long ll;
int n,m,q,x[N],y[N],op,a,b,c,d;
int lef[M],rig[M],up[M],dow[M];
int par[N*N];
ll sz[N*N],ans;
void ckmin(int &x,int y){x=min(x,y);}
void ckmax(int &x,int y){x=max(x,y);}
int find(int x){return par[x]==x?x:par[x]=find(par[x]);}
int f(int x,int y){return x*(d-1)+y;}
void unite(int x,int y){
    x=find(x),y=find(y);
    if(x==y)return;
    par[y]=x;sz[x]+=sz[y];
    ans=max(ans,sz[x]);
}
int main(){
    scanf("%d%d%d",&n,&m,&q);
    fill(rig,rig+m+1,n);
    fill(up,up+n+1,m);
    for(int i=1;i<=q;++i){
        scanf("%d%d%d",&a,&op,&b);
        int mx=(op<=2)?n:m;
        if(b==0 || b==mx)continue;
        if(op==1)ckmin(up[b],m-a);
        else if(op==2)ckmax(dow[b],a);
        else if(op==3)ckmax(lef[b],a);
        else if(op==4)ckmin(rig[b],n-a);
    }
    x[c++]=0;y[d++]=0;
    for(int i=1;i<n;++i)if(dow[i] || up[i]<m)x[c++]=i;
    for(int i=1;i<m;++i)if(lef[i] || rig[i]<n)y[d++]=i;
    x[c++]=n;y[d++]=m;
    for(int i=0;i<c-1;++i){
        for(int j=0;j<d-1;++j){
            int id=f(i,j);
            ll l=x[i+1]-x[i],r=y[j+1]-y[j];
            par[id]=id,sz[id]=l*r;
            ans=max(ans,sz[id]);
        }
    }
    for(int i=0;i<c-1;++i){
        for(int j=0;j<d-1;++j){
            int id=f(i,j),nid,lb;
            if(i+1<c-1){
                lb=x[i+1];
                if(dow[lb]<y[j+1] && up[lb]>y[j] && dow[lb]<up[lb]){
                    nid=f(i+1,j);
                    unite(id,nid);
                }
            }
            if(j+1<d-1){
                lb=y[j+1];
                if(lef[lb]<x[i+1] && rig[lb]>x[i] && lef[lb]<rig[lb]){
                    nid=f(i,j+1);
                    unite(id,nid);
                }
            }
        }
    }
    printf("%lld\n",ans);
    return 0;
}

代码2

自己赛中的乱搞，实际是ban掉了相邻块扩展的方向，在扩展的时候合并并查集连通块

#include<bits/stdc++.h>
using namespace std;
const int N=4e3+10;
typedef long long ll;
int n,m,q,x[N],y[N],op,a,b,c,d;
int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
bool ban[N*N][4];
int par[N*N];
ll sz[N*N],ans;
struct node{
    int a,op,b;
}e[N];
int find(int x){
    return par[x]==x?x:par[x]=find(par[x]);
}
int f(int x,int y){
    return x*(d-1)+y;
}
bool ok(int x,int y){
    return x>=0 && x<c-1 && y>=0 && y<d-1;
}
void unite(int x,int y){
    x=find(x),y=find(y);
    if(x==y)return;
    par[y]=x;sz[x]+=sz[y];
    ans=max(ans,sz[x]);
}
int main(){
    scanf("%d%d%d",&n,&m,&q);
    x[c++]=0;x[c++]=n;
    y[d++]=0;y[d++]=m;
    for(int i=1;i<=q;++i){
        scanf("%d%d%d",&a,&op,&b);
        e[i]={a,op,b};
        if(op==1 || op==2)x[c++]=b;
        else y[d++]=b;
        if(op==1 && m-a>=0)y[d++]=m-a;
        if(op==2 && a<=m)y[d++]=a;
        if(op==3 && a<=n)x[c++]=a;
        if(op==4 && n-a>=0)x[c++]=n-a;
    }
    sort(x,x+c);c=unique(x,x+c)-x;
    sort(y,y+d);d=unique(y,y+d)-y;
    //printf("c:%d d:%d\n",c,d);
    //for(int i=0;i<c;++i)printf("i:%d c:%d\n",i,x[i]);
    //for(int i=0;i<d;++i)printf("i:%d d:%d\n",i,y[i]);
    for(int i=1;i<=q;++i){
        int a=e[i].a,op=e[i].op,b=e[i].b;
        int z,l,r,id1,id2;
        if(op==1){
            z=lower_bound(x,x+c,b)-x;
            l=lower_bound(y,y+d,m-a)-y,r=d-1;//>=min
            if(z && z!=c-1){
                for(int j=l;j<r;++j){
                    id1=f(z-1,j),id2=f(z,j);
                    //printf("op1 id1:(%d,%d) id2:(%d,%d)\n",z-1,j,z,j);
                    ban[id1][0]=ban[id2][2]=1;
                }
            }
        }
        else if(op==2){
            z=lower_bound(x,x+c,b)-x;
            l=0,r=upper_bound(y,y+d,a)-y-1;//<=max
            if(z && z!=c-1){
                for(int j=l;j<r;++j){
                    //printf("op2 id1:(%d,%d) id2:(%d,%d)\n",z-1,j,z,j);
                    id1=f(z-1,j),id2=f(z,j);
                    ban[id1][0]=ban[id2][2]=1;
                }
            }
        }
        else if(op==3){
            z=lower_bound(y,y+d,b)-y;
            l=0,r=upper_bound(x,x+c,a)-x-1;//<=max
            if(z && z!=d-1){
                for(int j=l;j<r;++j){
                    //printf("op3 id1:(%d,%d) id2:(%d,%d)\n",j,z-1,j,z);
                    id1=f(j,z-1),id2=f(j,z);
                    ban[id1][1]=ban[id2][3]=1;
                }
            }
        }
        else{
            z=lower_bound(y,y+d,b)-y;
            l=lower_bound(x,x+c,n-a)-x,r=c-1;//>=min
            if(z && z!=d-1){
                for(int j=l;j<r;++j){
                    //printf("op4 id1:(%d,%d) id2:(%d,%d)\n",j,z-1,j,z);
                    id1=f(j,z-1),id2=f(j,z);
                    ban[id1][1]=ban[id2][3]=1;
                }
            }
        }
    }
    for(int i=0;i<c-1;++i){
        for(int j=0;j<d-1;++j){
            int id=f(i,j);
            ll l=x[i+1]-x[i],r=y[j+1]-y[j];
            //printf("i:%d j:%d l:%lld r:%lld\n",i,j,l,r);
            par[id]=id,sz[id]=l*r;
            ans=max(ans,sz[id]);
        }
    }
    for(int i=0;i<c-1;++i){
        for(int j=0;j<d-1;++j){
            int id=f(i,j);
            //printf("i:%d j:%d sz:%lld\n",i,j,sz[id]);
            for(int k=0;k<4;++k){
                int ni=i+dx[k],nj=j+dy[k];
                if(!ok(ni,nj))continue;
                if(ban[id][k])continue;
                //printf("i:%d j:%d ni:%d nj:%d\n",i,j,ni,nj);
                int nid=f(ni,nj);
                unite(id,nid);
            }
        }
    }
    printf("%lld\n",ans);
    return 0;
}